Во всех школах в старших классах проходят курс стереометрии, в котором рассматривают характеристики различных пространственных фигур. Данная статья посвящена изучению свойств одной из таких фигур. Рассмотрим, что такое правильная треугольная призма.
Призма в геометрии
Согласно стереометрическому определению, призма является объемной фигурой, состоящей из n параллелограммов и двух одинаковых n-угольных оснований, где n - это целое положительное число. Оба основания расположены в параллельных плоскостях, а параллелограммы соединяют попарно их стороны в единую фигуру.
 Вам будет интересно:Перипатетика - это философское учение Аристотеля
Вам будет интересно:Перипатетика - это философское учение Аристотеля
Любую призму можно получить следующим способом: следует взять плоский n-угольник и переместить его параллельно самому себе в другую плоскость. В процессе перемещения вершины n-угольника прочертят n отрезков, которые будут боковыми ребрами призмы.
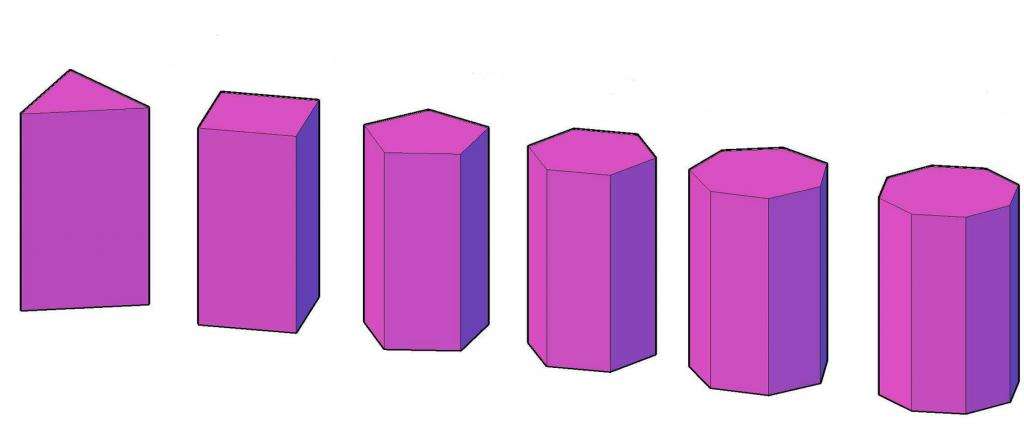
Призмы могут быть выпуклыми и вогнутыми, прямыми и косоугольными, правильными и неправильными. Все эти виды фигур отличаются друг от друга формой n-угольников в основании, а также их расположением относительно перпендикулярного им отрезка, длина которого является высотой призмы. Ниже рисунок демонстрирует набор призм с разным числом углов в основании и количеством боковых граней.
Правильная треугольная призма
Первая призма на фотографии выше является правильной треугольной. Она состоит из двух одинаковых равносторонних треугольников и из трех прямоугольников. Прямоугольник является частным случаем параллелограмма, поэтому рассматриваемая фигура удовлетворяет изложенному ранее стереометрическому определению.
Помимо пяти граней, треугольная призма образована шестью вершинами, которые принадлежат обоим основаниям, и девятью ребрами, три из которых являются боковыми.
Важным свойством правильной треугольной призмы является то, что ее высота совпадает с длиной бокового ребра. Все эти ребра равны друг другу, а боковые прямоугольники пересекают основания под прямыми углами. Отметим, что прямые двугранные углы между основаниями и боковыми гранями приводят к тому, что параллелограммы наклонной призмы становятся прямоугольниками в прямой фигуре. Очевидно, что при определенных длинах ребер прямоугольники могут стать квадратами.

Важными свойствами любой объемной фигуры являются площадь ее поверхности и заключенный в ней объем пространства. Изучаемая призма не является исключением, поэтому рассмотрим ее подробные характеристики.
Площадь поверхности
Площадь правильной треугольной призмы образована площадями всех ее пяти граней. Известно, что площадь пространственных фигур проще рассматривать и изучать на плоскости, поэтому удобно сделать развертку призмы. Она показана ниже.
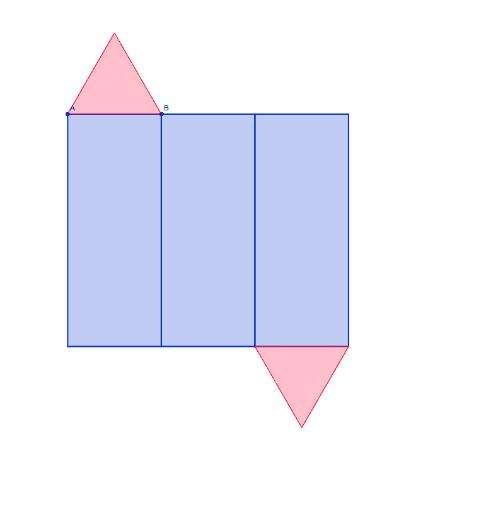
Развертка представлена пятью фигурами двух типов, которые в призме являлись гранями.
Для определения площади всех этих фигур введем следующие обозначения: будем считать длину стороны основания равной a, а высоту (длину бокового ребра) равной h. С учетом обозначений получаем площадь одного треугольника:
S3 = √3 / 4 × a2
При записи этой формулы использовалось стандартное выражение для площади треугольника. Площадь одного прямоугольника равна:
S4 = a × h
С учетом числа треугольников и прямоугольников (см. развертку выше) получим формулу для площади полной поверхности изучаемой геометрической фигуры:
S = 2 × S3 + 3 × S4 = √3 / 2 × a2 + 3 × a × h
Здесь первый член в правой части равенства описывает площадь двух оснований, второй член позволяет вычислить площадь поверхности боковой.
Напомним, что полученная для S формула справедлива только для прямой правильной треугольной призмы. Если бы мы рассматривали наклонную фигуру, то выражение для S имело бы другой вид.
Формула для определения объема фигуры
Объемом любой пространственной фигуры называется та часть пространства, которую ограничивают грани многогранника. Объем любой призмы, независимо от формы ее основания и боковых сторон, может быть определен по следующей формуле:
V = S0 × h
То есть достаточно умножить площадь одного основания на высоту всей фигуры, чтобы получить искомое значение объема.
Для случая треугольной правильной призмы получаем следующее выражение для V:
V = S0 × h = S3 × h = √3 / 4 × a2 × h
Записанная формула для V, а также выражение для S в предыдущем пункте зависят всего от двух параметров фигуры: длин a и h. То есть знание всего двух любых линейных параметров позволяет рассчитать все свойства изучаемой призмы.
Решение задачи
В физике треугольная правильная призма, изготовленная из сплошного стекла, часто применяется для разложения электромагнитного потока в видимой области спектра на ряд частот с целью их изучения. Необходимо определить, какой объем стекла понадобится, чтобы изготовить призму с площадью поверхности 300 см2 и длиной стороны основания 10 см.

Сначала определим высоту призмы h. Воспользуемся формулой для S, имеем:
S = √3 / 2 × a2 + 3 × a × h =>
h = (S - √3 / 2 × a2) / (3 × a) = (300 - √3 / 2 × 102) / (3 × 10) = 7,11 см
Поскольку мы знаем значения a и h, то для определения объема призмы воспользуемся формулой для V:
V = √3 / 4 × a2 × h = √3 / 4 × 102 × 7,11 = 307,87 см3
Таким образом, чтобы изготовить описанную призму, понадобится около 308 см3 стекла.