В физике, в разделах кинематики и динамики, изучают различные типы механического движения по разным видам траекторий. Данная статья посвящена рассмотрению графиков и формул равноускоренного движения тел по прямой траектории и по окружности.
Понятие об ускорении
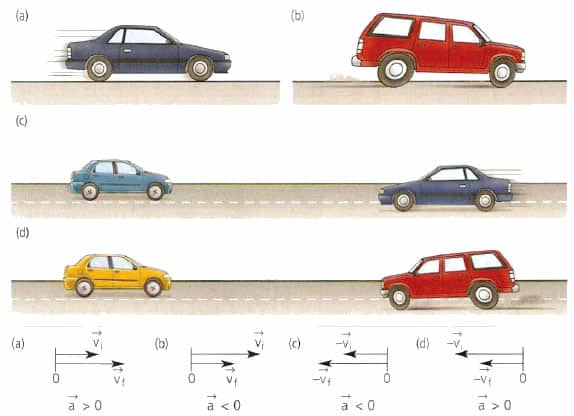
Прежде чем мы перейдем к анализу формул равноускоренного движения, следует дать определение самому ускорению. Под ним в физике полагают векторную величину, которая описывается изменение скорости во времени. Математическая формулировка этого определения выглядит так:
 Вам будет интересно:Мессбауэровская спектроскопия: понятие, особенности проведения, назначение и применение
Вам будет интересно:Мессбауэровская спектроскопия: понятие, особенности проведения, назначение и применение
a¯ = dv¯/dt.
Например, изменение скорости на 1 м/с за одну секунду характеризуется ускорением 1 м/с2.
Записанное выражение позволяет вычислить так называемую мгновенную скорость. На практике же часто необходимо знать не значение a¯ в данный момент времени, а некоторую среднюю величину acp¯ за определенный промежуток времени. В таком случае применяют следующую формулу:
a¯ = Δv¯/Δt.
Здесь Δv¯ - вектор изменения скорости за время Δt.
Отметим, что вектор ускорения всегда направлен в сторону изменения скорости, поэтому напрямую от вектора скорости он не зависит. В свою очередь, скорость направлена всегда по касательной к траектории в данной точке.
Движение равноускоренное прямолинейное
Данный вид движения часто появляется в физических задачах. На практике он также реализуется, например, при разгоне автомобиля с места, при свободном падении тяжелого тела или во время торможения транспортного средства. Во всех этих случаях речь идет о перемещении объектов с постоянным ускорением. Именно поэтому само движение называется равноускоренным (a = const).
Скорость и ускорение равноускоренного движения связаны следующим выражением:
v = v0 + a*t.
Здесь v0 - скорость, которую тело имело до появления ускорения a. При начале движения с ускорением из состояния относительного покоя значение v0 можно опустить. Тогда получим:
v = a*t.
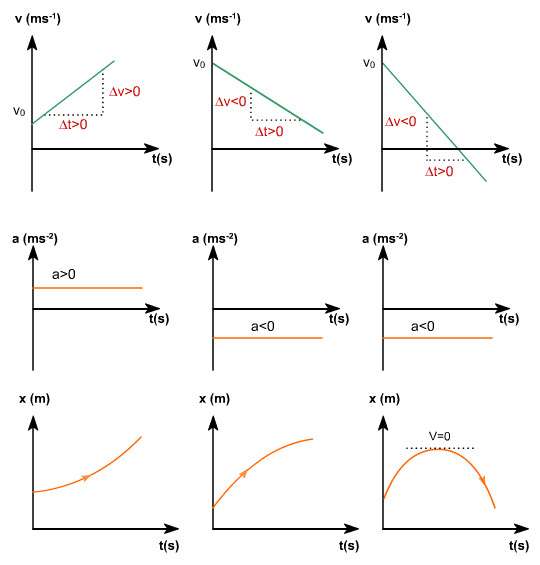
Как видно, графиками равноускоренного движения для функции v(t) будут прямые, которые начинаются либо из точки (0; v0), либо из точки (0; 0). Угол между осью абсцисс и прямой равен арктангенсу от значения ускорения.
В случае наличия начальной скорости v0, ускорение a может быть отрицательным, что на практике соответствует торможению тела. Графиком v(t) при этом будет также прямая линия, но она будет стремиться к нулевому значению скорости. Соответствующая формула принимает вид:
v = v0 - a*t.
Поскольку ускорение равноускоренного движения от времени не зависит, то графиком функции a(t) будет прямая, параллельная оси времени t.
Перемещение при равноускоренном движении прямолинейном
Выше были приведены три формулы равноускоренного движения по прямой, которые связывают скорость и время (ускорение - постоянная величина). Чтобы рассчитать путь, который тело пройдет за время t при таком типе перемещения, следует проинтегрировать записанные выражения по времени. В результате операции интегрирования мы получим следующие три формулы для пути S:
1) S = a*t2/2;
2) S = v0*t + a*t2/2;
3) S = v0*t - a*t2/2.
Все три выражения показывают, что для пути графики равноускоренного движения являются параболами, вернее, правой ее веткой. Для формул 1) и 2) речь идет о возрастающей ветви параболы, поскольку вектор ускорения совпадает с вектором скорости. Для третьего выражения правая ветвь параболы стремится к некоторому постоянному положительному значению S0, соответствующему пути, который тело пройдет до того, как полностью остановится.
Равноускоренное движение по окружности
Этот тип движения во многом отличается от прямолинейного. Во-первых, при ускоренном вращении скорость изменяет свой модуль и свой вектор, что приводит к появлению двух компонент ускорения: касательного и центростремительного. Во-вторых, при вращении нет никакого смысла оценивать, какое расстояние прошло тело, ведь оно движется под одной и той же окружности.
В связи со сказанным для описания движения по окружности пользуются угловыми скоростями и ускорениями. Угловое ускорение показывает, как быстро изменяется угловая скорость в радианах в секунду. С линейным ускорением a угловое α связано следующим выражением:
a = α*r.
Где r - радиус траектории вращения.
Для равноускоренного движения по круглой траектории справедливы следующие кинематические формулы:
θ = ω0*t ± α*t2/2;
ω = ω0 ± α*t.
Здесь θ - угол поворота в радианах за время t. Его можно использовать для вычисления линейного расстояния L, которое тело пройдет вдоль окружности:
L = θ*r.
Задача со свободным падением
Рассмотрев все важные формулы равноускоренного движения, решим такую задачу: тело брошено вертикально вверх с начальной скоростью 35 м/с. Необходимо определить, на какую высоту оно сможет подняться и через какое время оно упадет на землю. Силами трения можно пренебречь.
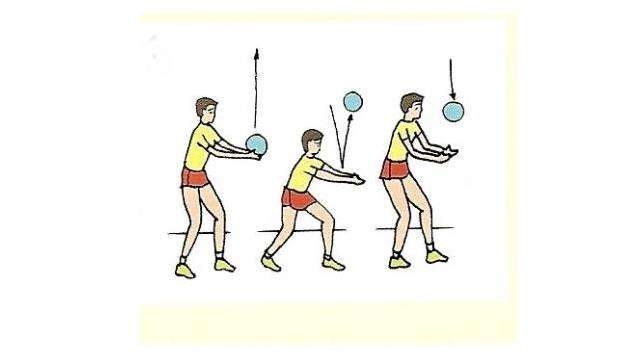
Во время подъема на тело действует ускорение свободного падения g, направленное против скорости, то есть время подъема будет равно:
v = v0 - g*t =>
t = v0/g.
Пренебрегая силами трения, можно с уверенностью сказать, что время подъема будет равно времени падения, поэтому полное время движения тела равно:
ttot = 2*t = 2*v0/g = 7,14 секунды.
Высоту подъема h можно вычислить по такой формуле:
h = v0*t - g*t2/2 = v02/(2*g) = 62,44 метра.
Таким образом, тело после броска вверх достигнет высоты 62,4 метра, и упадет на поверхность земли через 7,1 секунду после начала движения.