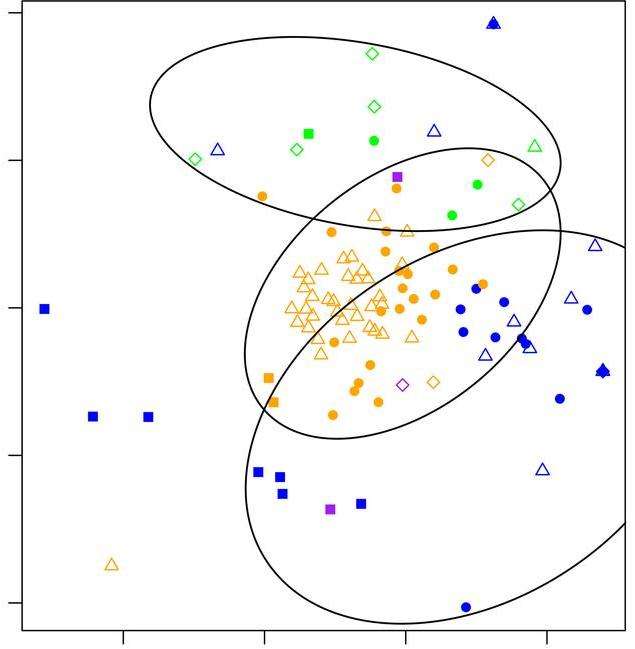
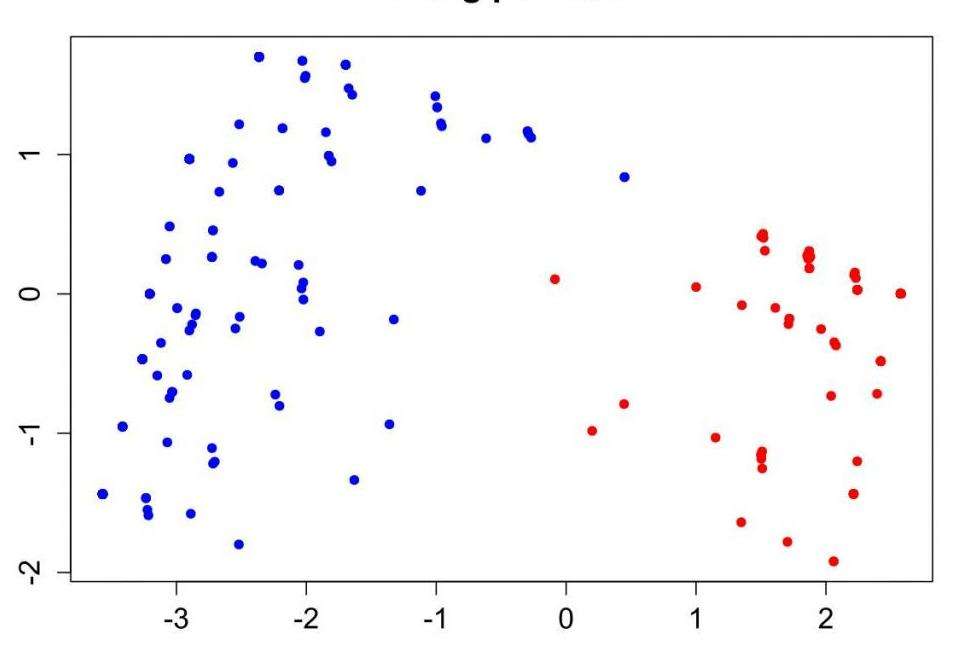
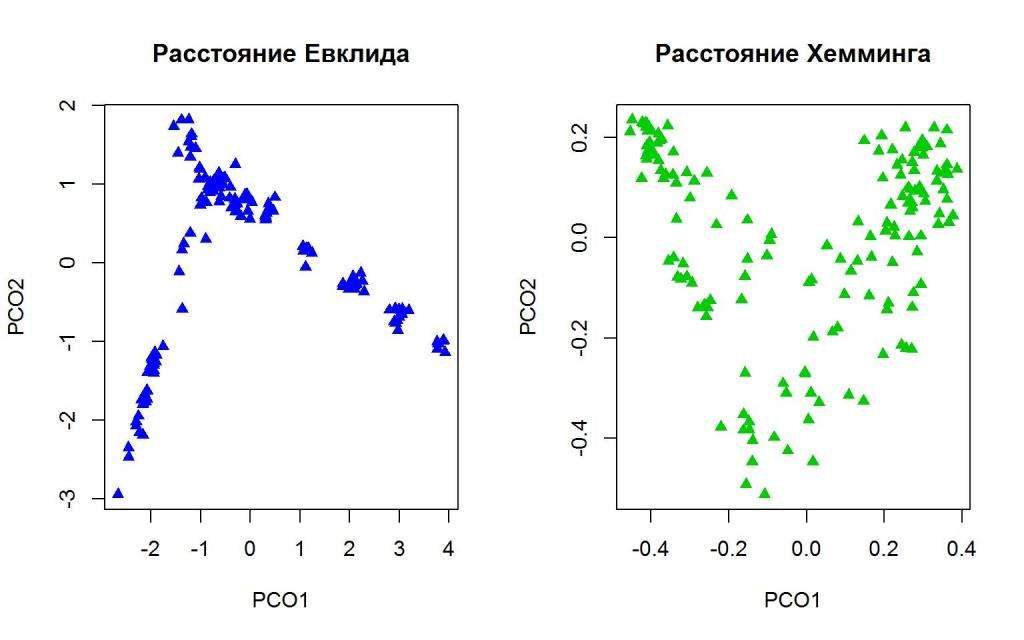
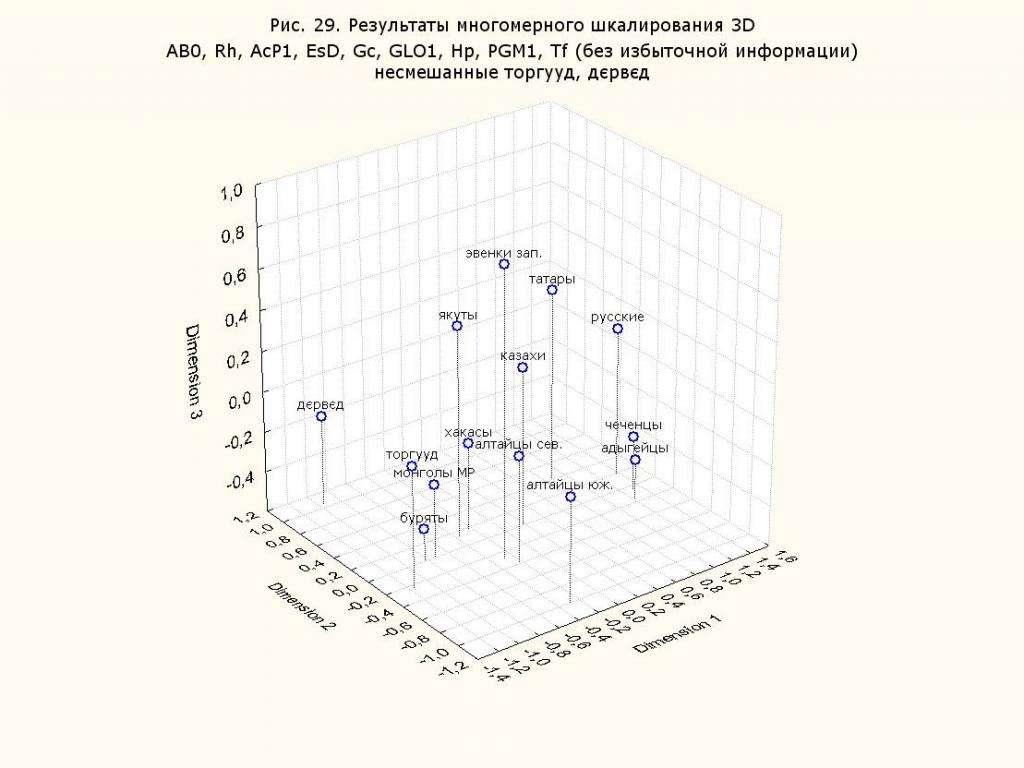
Многомерное шкалирование (MDS) - это средство визуализации уровня сходства отдельных случаев набора данных. Он относится к набору связанных методов ординации, используемых при визуализации информации, в частности, для отображения информации, содержащейся в матрице расстояний. Это форма нелинейного уменьшения размерности. Алгоритм MDS направлен на размещение каждого объекта в N-мерном пространстве таким образом, чтобы расстояния между объектами сохранялись как можно лучше. Затем каждому объекту присваиваются координаты в каждом из N измерений.
Вам будет интересно:Модель предметной области: понятие, структура и основные принципы
Количество измерений графика MDS может превышать 2 и указывается априори. Выбор N = 2 оптимизирует расположение объектов для двумерной диаграммы рассеяния. Примеры многомерного шкалирования вы можете увидеть на картинках в статье. Особенно показательны примеры с обозначениями на русском языке.
Суть
Метод многомерного шкалирования (ММШ, MDS) - это расширенный набор классических инструментов, который обобщает процедуру оптимизации для множества функций потерь и входных матриц известных расстояний с весами и так далее. В этом контексте полезная функция потерь называется стрессом, который часто сводится к минимуму с помощью процедуры, называемой мажоризацией стресса.
Руководство
Вам будет интересно:Давление газа - формула. Формула давления газа в сосуде
Существует несколько вариантов многомерного шкалирования. Программы MDS автоматически минимизируют нагрузку, чтобы получить решение. Ядро неметрического алгоритма MDS представляет собой двоякий процесс оптимизации. Во-первых, должно быть найдено оптимальное монотонное преобразование близости. Во-вторых, точки конфигурации должны быть расположены оптимально, чтобы их расстояния как можно ближе соответствовали масштабированным значениям близости.
Расширение
Расширение метрического многомерного шкалирования в статистике, в которой целевое пространство является произвольным гладким неевклидовым пространством. В тех случаях, когда отличия представляют собой расстояния на поверхности, а целевое пространство – это другая поверхность. Тематические программы позволяют находить вложение с минимальным искажением одной поверхности в другую.
Этапы
Вам будет интересно:Что такое похвала? Толкование слова
Есть несколько шагов в проведении исследования с помощью многомерного шкалирования:
Альтернативные подходы
Есть два других подхода. Существует методика под названием «Данные восприятия: производный подход», в которой продукты разлагаются на атрибуты, и оценка происходит по семантической дифференциальной шкале. Еще один метод – это «подход к данным о предпочтениях», при котором респондентам задают вопрос о предпочтениях, а не о сходстве.
Он состоит из следующих этапов:
Вам будет интересно:Долговязый — это? Толкование слова
Различные тесты
Другими возможными тестами являются стресс-тесты типа Kruskal, тесты на разделенные данные, тесты на стабильность данных и надежность повторного тестирования. Подробно пишите о результатах в тесте. Наряду с картированием должны быть указаны как минимум мера расстояния (например, индекс Соренсона, индекс Жакара) и надежность (например, значение напряжения).
Также очень желательно дать алгоритм (например, Kruskal, Mather), который часто определяется используемой программой (иногда заменяя отчет алгоритма), если вы дали стартовую конфигурацию или имели случайный выбор, количество прогонов размерности, результаты метода Монте-Карло, количество итераций, оценка устойчивости и пропорциональная дисперсия каждой оси (r-квадрат).
Визуальная информация и анализ данных методом многомерного шкалирования
Визуализация информации – это изучение интерактивных (визуальных) представлений абстрактных данных для усиления познания человека. Абстрактные данные включают как числовые, так и нечисловые данные, такие как текстовая и географическая информация. Однако информационная визуализация отличается от научной визуализации: «это информационный (информационная визуализация), когда выбрано пространственное представление, и scivis (научная визуализация), когда дано пространственное представление».
Область визуализации информации появилась в результате исследований в области взаимодействия человека с компьютером, прикладного использования информатики, графики, визуального дизайна, психологии и бизнес-методов. Она все чаще применяется в качестве важнейшего компонента в научных исследованиях, цифровых библиотеках, интеллектуальном анализе данных, финансовых данных, изучении рынка, контроле производства продукции и так далее.
Методы и принципы
Визуализация информации предполагает, что методы визуального представления и взаимодействия используют в своих интересах широкие возможности человеческого восприятия, позволяющие пользователям одновременно видеть, исследовать и понимать большие объемы информации. Визуализация информации направлена на создание подходов для передачи абстрактных данных, информации интуитивно понятным образом.
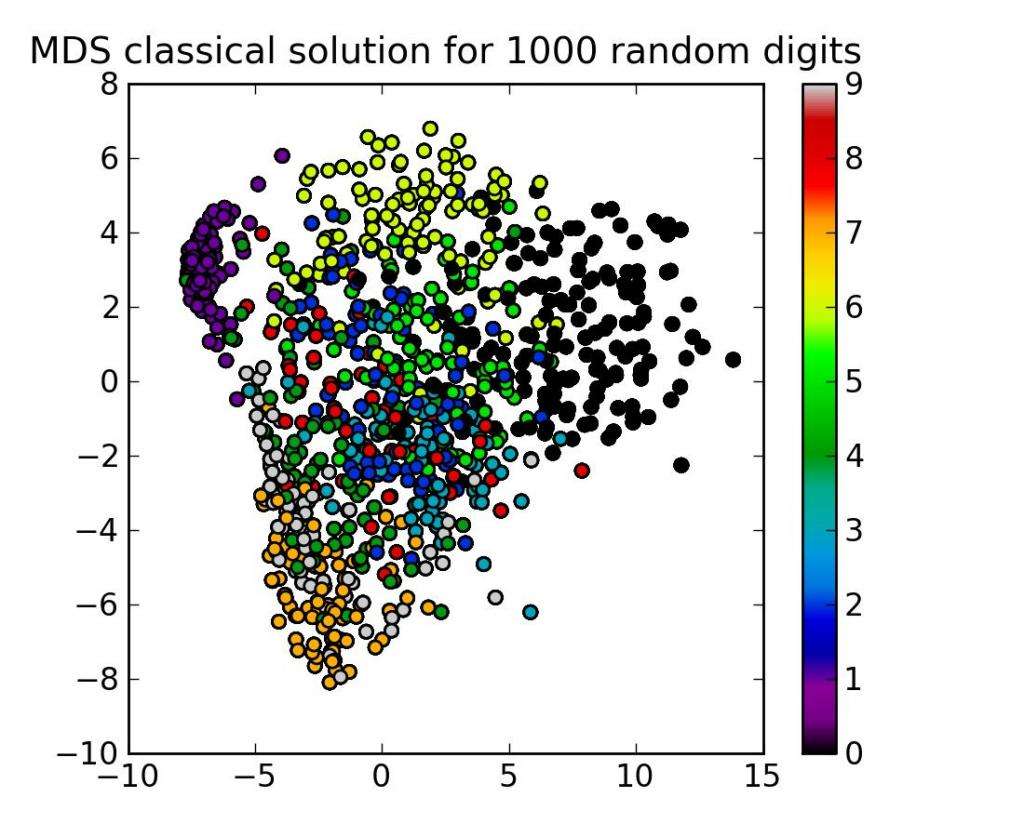
Анализ данных является неотъемлемой частью всех прикладных исследований и решения проблем в промышленности. Наиболее фундаментальными подходами к анализу данных являются визуализация (гистограммы, точечные диаграммы, графики поверхности, древовидные карты, параллельные координатные диаграммы и т. д.), статистика (проверка гипотез, регрессия, PCA и т. д.), анализ данных (сопоставление и т. д.) и методы машинного обучения (кластеризация, классификация, деревья решений и т. д.).
Среди этих подходов визуализация информации или визуальный анализ данных наиболее зависят от когнитивных навыков аналитического персонала и позволяют обнаруживать неструктурированные действенные идеи, которые ограничены только человеческим воображением и творчеством. Аналитик не должен изучать какие-либо сложные методы, чтобы иметь возможность интерпретировать визуализации данных. Визуализация информации также является схемой генерации гипотез, которая может сопровождаться и обычно сопровождается более аналитическим или формальным анализом, таким как статистическая проверка гипотез.
Изучение
Современное изучение визуализации началось с компьютерной графики, которая "с самого начала использовалась для изучения научных проблем. Однако в первые годы недостаток графической мощности часто ограничивал ее полезность. Приоритет на визуализации начал развиваться в 1987 году, с выпуска особого ПО для компьютерной графики и визуализации в научных вычислениях. С тех пор было проведено несколько конференций и семинаров, совместно организованных IEEE Computer Society и ACM SIGGRAPH".
Они были посвящены общим темам визуализации данных, визуализации информации и научной визуализации, а также более конкретным областям, таким как визуализация объема.
Обобщение
Обобщенное многомерное шкалирование (ОМШ, GMDS) является расширением метрического многомерного масштабирования, в котором целевое пространство неевклидово. Когда различия представляют собой расстояния на поверхности, а целевое пространство – это другая поверхность, GMDS позволяет находить вложение с минимальным искажением одной поверхности в другую.
GMDS – это новое направление исследований. В настоящее время основными приложениями являются распознавание деформируемых объектов (например, для трехмерного распознавания лиц) и наложение текстуры.
Целью многомерного шкалирования является представление многомерных данных. Многомерные данные, то есть данные, для представления которых требуется более двух или трех измерений, бывает трудно интерпретировать. Один из подходов к упрощению состоит в том, чтобы предположить, что интересующие данные лежат на вложенном нелинейном многообразии в многомерном пространстве. Если коллектор имеет достаточно низкое измерение, данные могут быть визуализированы в низкоразмерном пространстве.
Многие из нелинейных методов уменьшения размерности связаны с линейными методами. Нелинейные методы можно в целом классифицировать на две группы: те, которые обеспечивают отображение (либо из многомерного пространства в низкоразмерное вложение, или наоборот), и те, которые просто дают визуализацию. В контексте машинного обучения методы отображения могут рассматриваться как предварительный этап выделения признаков, после которого применяются алгоритмы распознавания образов. Обычно те, которые просто дают визуализацию, основаны на данных о близости – то есть измерения расстояния. Многомерное шкалирование в психологии и прочих гуманитарных науках также весьма распространено.
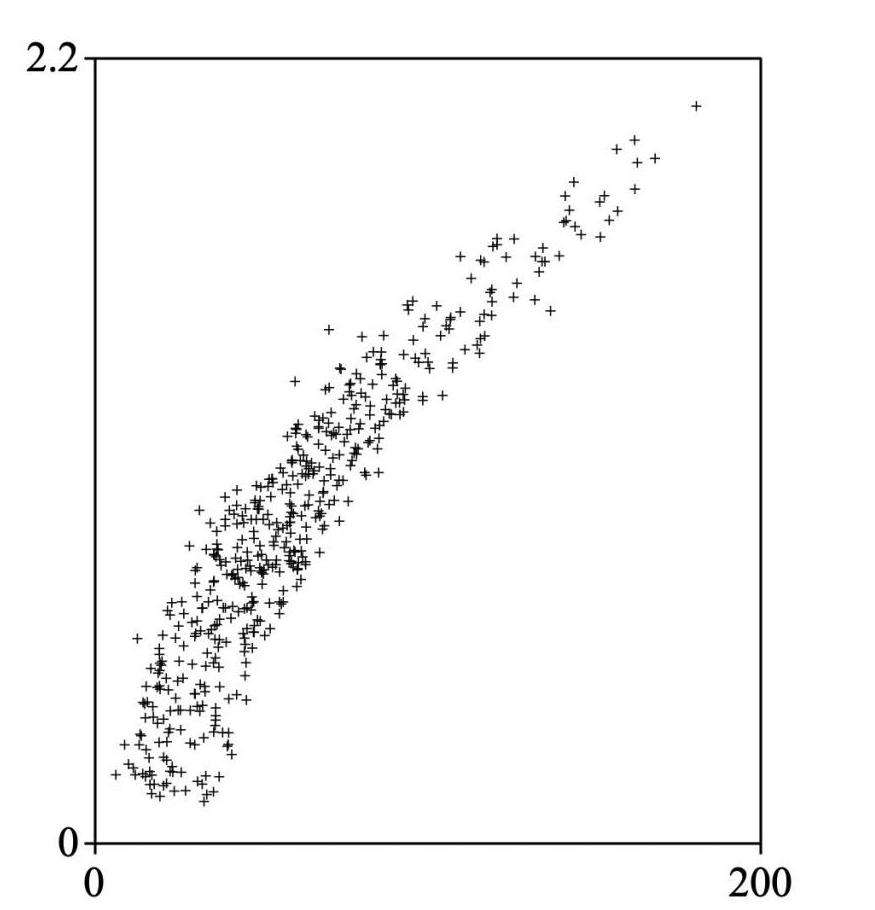
Если количество атрибутов велико, то пространство уникальных возможных строк также экспоненциально велико. Таким образом, чем больше размерность, тем сложнее становится изобразить пространство. Это вызывает много проблем. Алгоритмы, которые работают с многомерными данными, имеют тенденцию к очень высокой временной сложности. Сокращение данных до меньшего числа измерений часто делает алгоритмы анализа более эффективными и может помочь алгоритмам машинного обучения делать более точные прогнозы. Потому многомерное шкалирование данных столь популярно.