- Основные понятия
- Ступенчатый вид матрицы
- Приведение матрицы к ступенчатой форме
- Матрицы и системы линейных уравнений
- Общая информация о методе Гаусса
- Пример решения СЛУ методом Гаусса
- Метод Гаусса – Жордана
- Пример нахождения обратной матрицы методом Гаусса – Жордана
- Пример решения СЛУ методом Гаусса – Жордана
- Онлайн-калькуляторы
Линейная алгебра, которая преподается в вузах на разных специальностях, объединяет немало сложных тем. Одни из них связаны с матрицами, а также с решением систем линейных уравнений методами Гаусса и Гаусса – Жордана. Не всем студентам удается понять эти темы, алгоритмы решения разных задач. Давайте вместе разберемся в матрицах и методах Гаусса и Гаусса – Жордана.
Основные понятия
Под матрицей в линейной алгебре понимается прямоугольный массив элементов (таблица). Ниже представлены наборы элементов, заключенные в круглые скобки. Это и есть матрицы. Из приведенного примера видно, что элементами в прямоугольных массивах являются не только числа. Матрица может состоять из математических функций, алгебраических символов.
 Вам будет интересно:Вглядитесь внимательно. Не попались ли среди встречных шедшие на вы?
Вам будет интересно:Вглядитесь внимательно. Не попались ли среди встречных шедшие на вы?
Для того чтобы разобраться с некоторыми понятиями, составим матрицу A из элементов aij. Индексы являются не просто буквами: i – это номер строки в таблице, а j – это номер столбца, в области пересечения которых располагается элемент aij. Итак, мы видим, что у нас получилась матрица из таких элементов, как a11, a21, a12, a22 и т. д. Буквой n мы обозначили число столбцов, а буквой m – число строк. Символ m × n обозначает размерность матрицы. Это то понятие, которое определяет число строк и столбцов в прямоугольном массиве элементов.
Необязательно в матрице должно быть несколько столбцов и строк. При размерности 1 × n массив элементов является однострочным, а при размерности m × 1 – одностолбцовым. При равенстве числа строчек и числа столбцов матрицу именуют квадратной. У каждой квадратной матрицы есть определитель (det A). Под этим термином понимается число, которое ставится в соответствие матрице A.
Еще несколько важных понятий, которые нужно запомнить для успешного решения матриц, – это главная и побочная диагонали. Под главной диагональю матрицы понимается та диагональ, которая идет вниз в правый угол таблицы из левого угла сверху. Побочная диагональ идет в правый угол вверх из левого угла снизу.
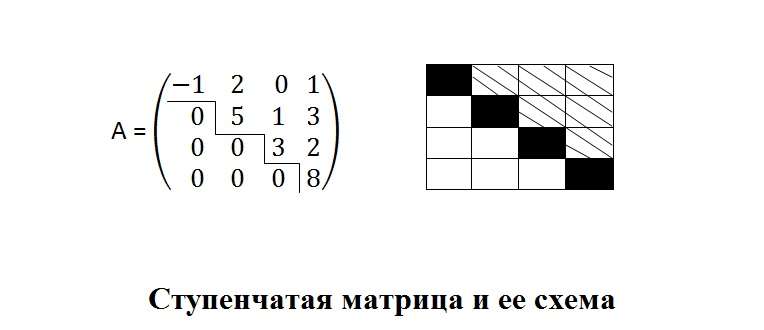
Ступенчатый вид матрицы
Взгляните на картинку, которая представлена ниже. На ней вы увидите матрицу и схему. Разберемся сначала с матрицей. В линейной алгебре матрица подобного вида называется ступенчатой. Ей присуще одно свойство: если aij является в i-й строке первым ненулевым элементом, то все другие элементы из матрицы, стоящие ниже и левее aij, являются нулевыми (т. е. все те элементы, которым можно дать буквенное обозначение akl, где k>i, а l Теперь рассмотрим схему. Она отражает ступенчатую форму матрицы. В схеме представлено 3 вида клеток. Каждый вид обозначает определенные элементы: При решении матриц иногда получается такой результат, когда «длина» ступеньки оказывается больше 1. Такое допускается. Важна лишь «высота» ступенек. В матрице ступенчатого вида этот параметр должен быть всегда равным единице. Любая прямоугольная матрица может быть преобразована до ступенчатого вида. Делается это благодаря элементарным преобразованиям. Они включают в себя: Рассмотрим элементарные преобразования в решении конкретной задачи. На рисунке ниже представлена матрица A, которую требуется привести к ступенчатому виду. Для того чтобы решить задачу, будем следовать алгоритму: Приведение матриц к ступенчатой форме используется в решении систем линейных уравнений (СЛУ) методом Гаусса. Перед рассмотрением этого метода давайте разберемся в терминах, имеющих отношение к СЛУ. Матрицы применяются в разных науках. С использованием таблиц из чисел можно, например, решать линейные уравнения, объединенные в систему, методом Гаусса. Для начала давайте познакомимся с несколькими терминами и их определениями, а также посмотрим, как из системы, объединяющей несколько линейных уравнений, составляется матрица. СЛУ – несколько объединенных алгебраических уравнений, в которых присутствуют неизвестные в первой степени и отсутствуют члены, представляющие собой произведение неизвестных. Решение СЛУ – найденные значения неизвестных, при подстановке которых уравнения в системе становятся тождествами. Совместная СЛУ – такая система уравнений, у которой есть хотя бы одно решение. Несовместная СЛУ – система уравнений, которая не имеет решений. Как же составляется матрица на основе системы, объединяющей линейные уравнения? Существуют такие понятия, как основная и расширенная матрицы системы. Для того чтобы получить основную матрицу системы, необходимо вынести в таблицу все коэффициенты при неизвестных. Расширенная матрица получается путем присоединения к основной матрице столбца свободных членов (в него входят известные элементы, к которым в системе приравнивается каждое уравнение). Понять весь этот процесс можно, изучив картинку ниже. Первое, что мы видим на картинке, – это систему, включающую в себя линейные уравнения. Ее элементы: aij – числовые коэффициенты, xj – неизвестные величины, bi – свободные члены (где i = 1, 2, …, m, а j = 1, 2, …, n). Второй элемент на картинке – основная матрица из коэффициентов. Из каждого уравнения коэффициенты записываются в строку. В итоге получается в матрице столько строк, сколько уравнений входит в систему. Количество столбцов равно наибольшему количеству коэффициентов в каком-либо уравнении. Третий элемент на картинке – расширенная матрица со столбцом свободных членов. В линейной алгебре методом Гаусса называется классический способ решения СЛУ. Он носит имя Карла Фридриха Гаусса, жившего в XVIII–XIX вв. Это один из величайших математиков всех времен. Суть метода Гаусса заключается в выполнении элементарных преобразований над системой линейных алгебраических уравнений. С помощью преобразований СЛУ приводится к равносильной системе треугольной (ступенчатой) формы, из которой можно найти все переменные. Стоит отметить, что Карл Фридрих Гаусс не является первооткрывателем классического способа решения системы линейных уравнений. Метод был придуман намного раньше. Первое его описание встречается в энциклопедии знаний древнекитайских математиков, носящей название «Математика в 9 книгах». Рассмотрим на конкретном примере решение систем методом Гаусса. Будем работать с СЛУ, представленной на картинке. Алгоритм решения: Ответ: используя матрицу, метод Гаусса, мы нашли значения неизвестных; x1 = –1, x2 = 0, x3 = 1. В линейной алгебре есть еще такое понятие, как метод Гаусса – Жордана. Он считается модификацией метода Гаусса и применяется при нахождении обратной матрицы, вычислении неизвестных членов квадратных систем алгебраических линейных уравнений. Метод Гаусса – Жордана удобен тем, что он в один этап позволяет решить СЛУ (без применения прямого и обратного ходов). Начнем с термина «обратная матрица». Допустим, у нас есть матрица A. Обратной для нее будет матрица A-1, при этом обязательно выполняется условие: A × A-1 = A-1 × A = E, т. е. произведение этих матриц равно единичной матрице (у единичной матрицы элементы главной диагонали являются единицами, а остальные элементы равны нулю). Важный нюанс: в линейной алгебре есть теорема существования обратной матрицы. Достаточное и необходимое условие существования матрицы A-1 – невырожденность матрицы A. При невырожденности det A (определитель) не равен нулю. Основные шаги, на которых основывается метод Гаусса – Жордана: Для вычисления обратной матрицы нужно записать расширенную матрицу A|E и выполнить необходимые преобразования. Рассмотрим простой пример. На рисунке ниже представлена матрица A. Решение: На рисунке представлена система линейных уравнений. Требуется найти значения неизвестных переменных, используя матрицу, метод Гаусса – Жордана. Решение: При желании можно проверить правильность решения, подставив вычисленные значения в уравнения: Вывод: используя метод Гаусса – Жордана, мы нашли правильное решение квадратной системы, объединяющей линейные алгебраические уравнения. Жизнь современной молодежи, обучающейся в вузах и изучающей линейную алгебру, значительно упростилась. Еще несколько лет назад находить решения систем методом Гаусса и Гаусса – Жордана приходилось самостоятельно. Одни студенты успешно справлялись с задачами, а другие путались в решении, делали ошибки, просили у однокурсников помощи. Сегодня можно при выполнении домашнего задания пользоваться онлайн-калькуляторами. Для решения систем линейных уравнений, поиска обратных матриц написаны программы, которые демонстрируют не только правильные ответы, но и показывают ход решения той или иной задачи. В интернете есть немало ресурсов со встроенными онлайн-калькуляторами. Матрицы методом Гаусса, системы уравнений решаются этими программами за несколько секунд. Студентам требуется только указывать необходимые параметры (например, количество уравнений, количество переменных).
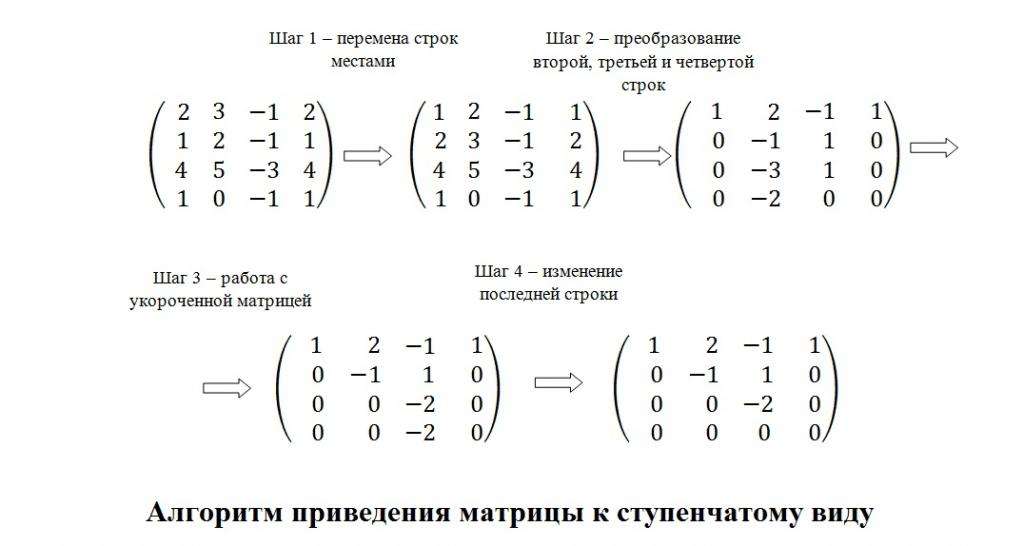
Приведение матрицы к ступенчатой форме

Матрицы и системы линейных уравнений
Общая информация о методе Гаусса
Пример решения СЛУ методом Гаусса
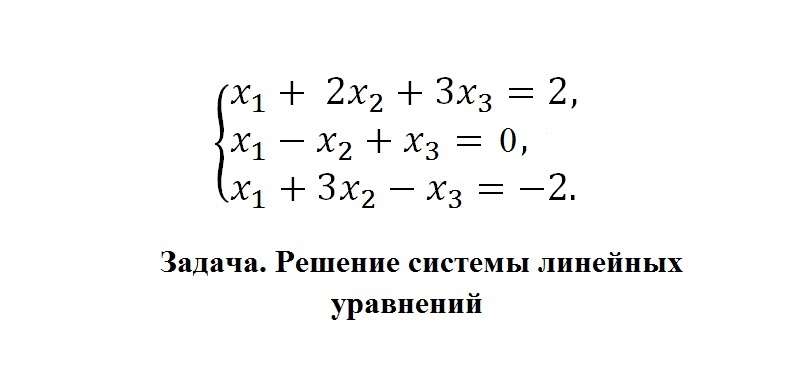
Метод Гаусса – Жордана
Пример нахождения обратной матрицы методом Гаусса – Жордана

Пример решения СЛУ методом Гаусса – Жордана


Онлайн-калькуляторы