Одной из важных физических характеристик, которые используются при кинематическом и динамическом описании механического движения тел, является импульс. В данной статье приведем определение закона сохранения импульса в физике, а также продемонстрируем на примере задачи, как его можно использовать на практике.
Импульс или количество движения
Прежде чем рассматривать формулу и определение закона сохранения импульса, познакомимся с самой величиной. В физике под механическим импульсом принято понимать произведение инерционной массы тела на линейную скорость его перемещения в пространстве. Математически величина записывается так:
 Вам будет интересно:Расчет мощности двигателя: методики и необходимые формулы
Вам будет интересно:Расчет мощности двигателя: методики и необходимые формулы
p¯ = m*v¯.
Как видно, импульс p¯ является векторной характеристикой. Его направление совпадает со скоростью, а модуль в m раз больше модуля |v¯|. Формула показывает, что p¯ содержит информацию одновременно о кинетических и инерционных свойствах тела.
Впервые об импульсе заговорили ученые Нового времени. Первым из них стал Галилео Галилей. В одном из своих научных трудов он использовал эту величину при описании движения тел. Называл он ее количеством движения. Впоследствии Исаак Ньютон взял ее на вооружение при формулировании базовых законов механики.
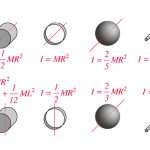 Вам будет интересно:Момент инерции материальной точки и твердого тела: формулы, теорема Штейнера, пример решения задачи
Вам будет интересно:Момент инерции материальной точки и твердого тела: формулы, теорема Штейнера, пример решения задачи
Изменение количества движения
Напомним, что первый ньютоновский закон говорит о том, что тело не изменяет своей скорости по модулю и направлению до тех пор, пока на него не начнет действовать какая-нибудь внешняя сила. Поскольку масса движущегося тела в механике также остается постоянной, то количество движения p меняться не будет.
Как только некоторая внешняя сила воздействует на тело, то в соответствии со вторым ньютоновским законом она приведет к появлению линейного ускорения. Математически имеем следующие равенства:
F = m*a = m*dv/dt = dp/dt =>
dp = F*dt.
Мы пришли к интересному выводу: оказывается, что величина изменения количества движения будет равна произведению силы на время ее действия. Это произведение называется импульсом силы. Отсюда получаем название импульса для изменения количества движения dp.
Определение закона сохранения импульса
Итак, мы рассмотрели саму физическую величину, показали, в каких условиях количество движения одного тела может измениться. А что будет с системой движущихся тел, если их предоставить самим себе? Поскольку система является закрытой, то есть на нее не воздействуют внешние силы, то полное количество движения всех тел изменяться во времени не будет, несмотря на то, что между самими телами могут происходить взаимодействия. Последние представляют собой упругие или пластические столкновения тел. Если во время движения тел в системе присутствуют рассеивающие силы, например, сила трения, то полный импульс сохраняться не будет.
В соответствии с определением закона сохранения импульса, формула математическая для него записывается в виде:
p¯ = const.
Поскольку неизменной остается каждая компонента величины p¯, то для практики удобнее пользоваться следующей системой равенств:
px = const;
py = const;
pz = const.
Отметим, что под компонентой импульса pi, где i = x, y, z, здесь понимается сумма всех соответствующих компонент импульсов для каждого тела, которое входит в изучаемую систему.
В физике обычно встречаются задачи с одномерным или двумерным характером движения, поэтому для их решения достаточно рассмотреть систему из одного или двух уравнений.
Упругие и пластические столкновения
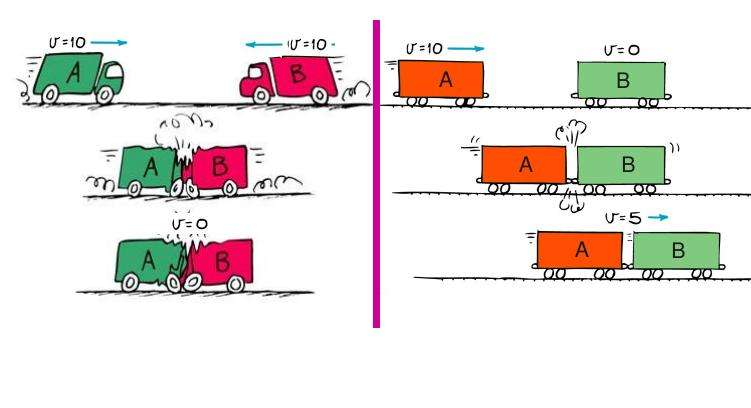
Выше при рассмотрении определения закона сохранения импульса было сказано, что он выполняется при упругих и пластических столкновениях. Поясним этот момент.
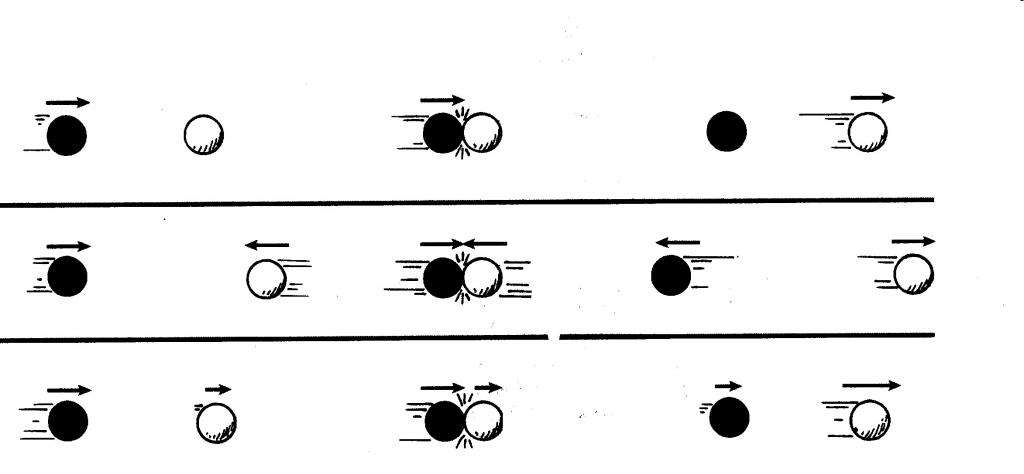
Представим себе движение двух шаров навстречу друг другу. Если в результате их столкновения суммарная кинетическая энергия не изменилась, то имело место упругое столкновения. Любое уменьшение кинетической энергии говорит о наличие пластической деформации у тел после столкновения. Абсолютно неупругим называется такое столкновение, после которого два шара (тела) начинают двигаться как единое целое.
Для определения степени пластичности столкновения двух тел вводят специальную величину, которая называется коэффициентом восстановления. Этот коэффициент равен отношению разности скоростей тел после соударения к разности их скоростей до соударения, которое нужно взять с обратным знаком. Коэффициент изменяется от 0 до 1, причем эти цифры соответствуют абсолютно пластичному и упругому столкновениям, соответственно. Закон сохранения количества движения остается справедливым для любого значения коэффициента восстановления.
Пример решения задачи
Решим следующую простую физическую проблему на применение полученных знаний. Предположим, что два шара движутся друг на друга. Массы шаров равны 5 кг и 3 кг. Их скорости составляют 4 м/с и 6 м/с. После абсолютно пластичного соударения оба шара начинают двигаться вместе. Необходимо определить направление и скорость их совместного движения.
Для решения задачи сделаем следующие обозначения:
v1 = 4 м/с, m1 = 5 кг;
v2 = 6 м/с, m2 = 3 кг.
Предположим, что первый шар движется слева направо, а второй в противоположном направлении. Тогда получаем:
m1*v1 - m2*v2 = (m1 + m2)*u =>
u = (m1*v1 - m2*v2)/(m1 + m2) = (5*4 - 3*6)/(5+3) = 2/8 = 0,25 м/с.
Поскольку получено положительное значение скорости, то это означает, что оба шара после соударения будут двигаться слева направо.
Закон сохранения момента импульса
Определение математическое момента импульса точки материальной можно дать следующее:
L = p*r.
Где буквой r обозначен радиус вращения материальной точки вокруг оси.
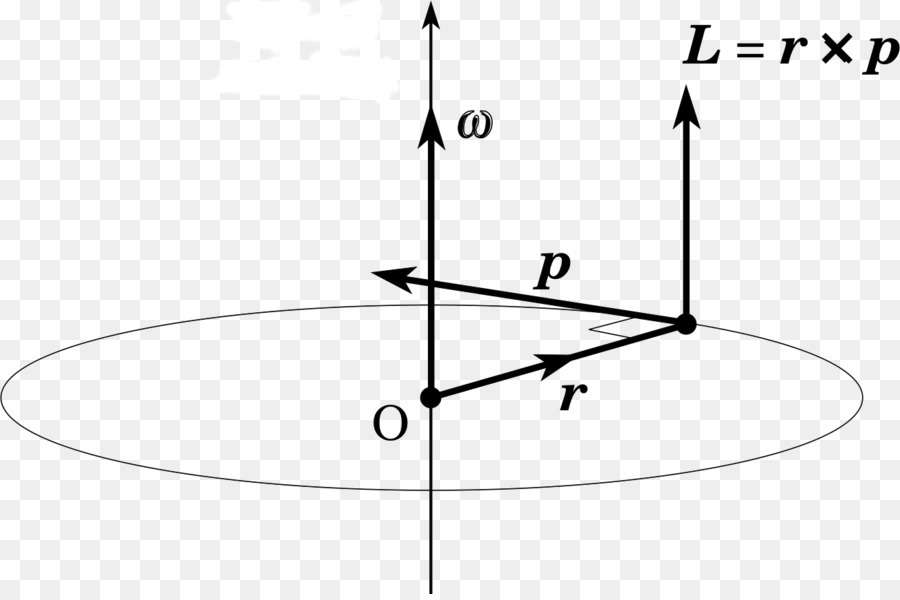
Так же как и линейный импульс, величина L сохраняется только тогда, когда на систему не действуют внешние моменты сил. Под моментом силы полагают величину, равную произведению силы на радиус ее приложения относительно оси вращения. Соответствующий закон сохранения записывают так:
I*ω = const.
Где I - это момент инерции, ω - скорость угловая.
Люди, которые любят смотреть фигурное катание, наверняка, не раз замечали этот закон в действии, когда спортсмен, изменяя положение своего тела, начинал вращаться на льду быстрее или медленнее.