Объем и площадь поверхности - это две важные характеристики любого тела, имеющего конечные размеры в трехмерном пространстве. В данной статье рассмотрим известный класс многогранников - призмы. В частности, будет раскрыт вопрос, как найти площадь поверхности прямой призмы.
Что собой представляет призма?
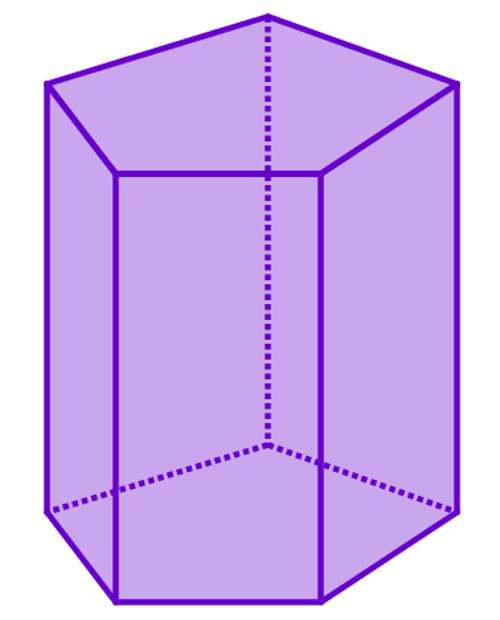
Призмой называется любой многогранник, который ограничен несколькими параллелограммами и двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. Эти многоугольники считают основаниями фигуры, а ее параллелограммы - это боковые стороны. Количество сторон (углов) основания определяет название фигуры. Например, на рисунке ниже изображена пятиугольная призма.
 Вам будет интересно:Цитаты про баскетбол со смыслом
Вам будет интересно:Цитаты про баскетбол со смыслом
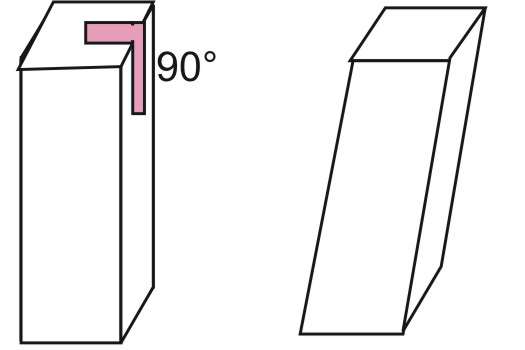
Расстояние между основаниями называется высотой фигуры. Если высота равна длине любого бокового ребра, то такая призма будет прямой. Вторым достаточным признаком для прямой призмы является то, что у нее все боковые стороны представляют собой прямоугольники или квадраты. Если же хотя бы одна боковая сторона является параллелограммом общего вида, то фигура будет наклонной. Ниже можно посмотреть, как визуально отличаются прямая и наклонная призмы на примере четырехугольных фигур.
Площадь поверхности прямой призмы
Если геометрическая фигура имеет n-угольное основание, тогда она состоит из n+2 граней, n из которых являются прямоугольниками. Обозначим длины сторон основания символом ai, где i = 1,2,...,n, а высоту фигуры, которая равна длине бокового ребра, обозначим h. Чтобы определить площадь (S) поверхности всех граней, необходимо сложить площадь So каждого из оснований и все площади боковых сторон (прямоугольников). Таким образом, формулу для S в общем виде можно записать так:
S = 2*So + Sb
Где Sb - площадь боковой поверхности.
Поскольку основанием прямой призмы может быть совершенно любой плоский многоугольник, то единой формулы для вычисления So привести нельзя, и для определения этой величины в общем случае следует проводить геометрический анализ. Например, если основание представляет собой правильный n-угольник со стороной a, тогда его площадь вычисляется по формуле:
So = n/4*ctg(pi/n)*a2
Что касается величины Sb, то выражение для ее вычисления привести можно. Площадь боковой поверхности прямой призмы равна:
Sb = h*∑i=1n(ai)
То есть величина Sb вычисляется как произведение высоты фигуры на периметр ее основания.
Пример решения задачи
Применим полученные знания для решения следующей геометрической задачи. Дана призма, основание которой представляет собой прямоугольный треугольник со сторонами при прямом угле 5 см и 7 см. Высота фигуры составляет 10 см. Необходимо найти площадь поверхности прямой призмы треугольной.
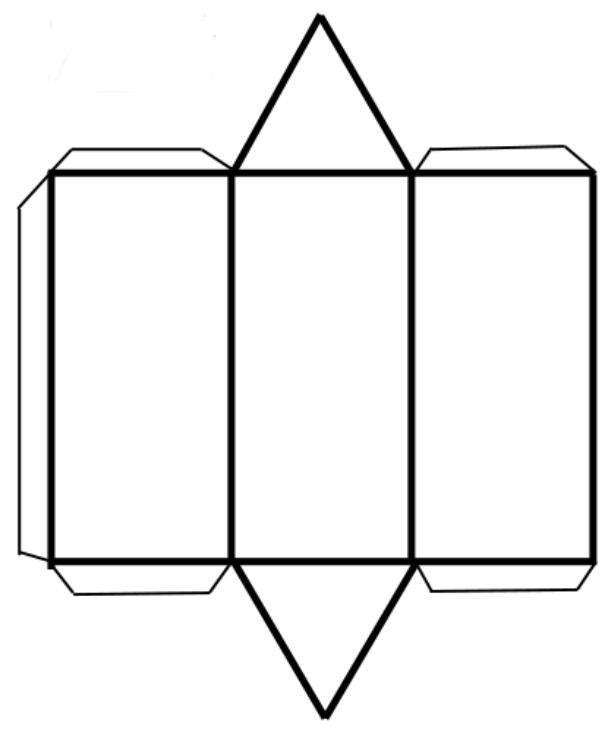
Для начала вычислим гипотенузу треугольника. Она будет равна:
c = √(52 + 72) = 8,6 см
Теперь сделаем еще одну подготовительную математическую операцию - рассчитаем периметр основания. Он составит:
P = 5 + 7 + 8,6 = 20,6 см
Площадь боковой поверхности фигуры вычисляется как произведение величины P на высоту h=10 см, то есть Sb = 206 см2.
Чтобы найти площадь всей поверхности, к найденной величине следует добавить две площади основания. Поскольку площадь прямоугольного треугольника определяется половиной произведения катетов, то получаем:
2*So = 2*5*7/2 = 35 см2
Тогда получаем, что площадь поверхности прямой призмы треугольной составляет 35 + 206 = 241 см2.