Пирамида вместе с призмой является совершенным полиэдром в трехмерном пространстве, геометрические характеристики их изучают в старших классах школы. В данной статье рассмотрим, какие бывают пирамиды, из каких элементов они состоят, а также охарактеризуем кратко правильные пирамиды.
Геометрическая фигура пирамида
С точки зрения геометрии пирамида является пространственной фигурой, состоящей из одного многоугольника и нескольких треугольников. Получить эту фигуру достаточно просто. Для этого следует взять многоугольник с n сторонами, затем выбрать произвольную точку пространства, которая не будет лежать в плоскости многоугольника, и соединить каждую вершину многоугольника с этой точкой. Очевидно, что образованная таким образом фигура будет иметь n треугольников, соединенных друг с другом в одной вершине.
 Вам будет интересно:«Пассивный» — это плохая характеристика для человека?
Вам будет интересно:«Пассивный» — это плохая характеристика для человека?
Чтобы наглядно представить геометрическую форму описанной фигуры, приведем рисунок.

Здесь показана четырехугольная пирамида, основание которой представляет собой четырехугольник, а боковая поверхность образована четырьмя треугольниками, имеющими общую вершину.
Элементы пирамиды
Как и всякий полиэдр, пирамида образована тремя видами элементов:
- гранями;
- вершинами;
- ребрами.
Грани - это части плоскостей, которые отделяют внутренний объем фигуры от окружающего пространства. Если пирамида в основании содержит n-угольник, то число ее граней всегда равно n+1. Из них n сторон являются треугольными, а одна сторона - упомянутое n-угольное основание.
Вершины - точки, где пересекаются три и более грани фигуры. В области основания содержится n вершин, каждая из которых образована двумя треугольными гранями и основанием. Точка, где соединяются n треугольных сторон, получила название вершины пирамиды. Таким образом, рассматриваемая фигура состоит из n+1 вершин.
Ребра - прямые отрезки, которые появляются при пересечении двух граней. Каждое ребро со своих концов ограничено двумя вершинами. Любая пирамида с n-угольником в основании содержит 2*n ребер. Половина из этого количества, то есть n, образована исключительно пересечением боковых треугольников.
Возможные виды фигуры
Название рассматриваемой фигуры однозначно определяется типом многоугольника в основании. Например, если он имеет три угла и три стороны, то пирамида будет треугольной, если четыре - четырехугольной, и так далее.
Многоугольник может быть выпуклым и вогнутым, а также правильным и общего типа. Все это также определяет вид пирамиды.
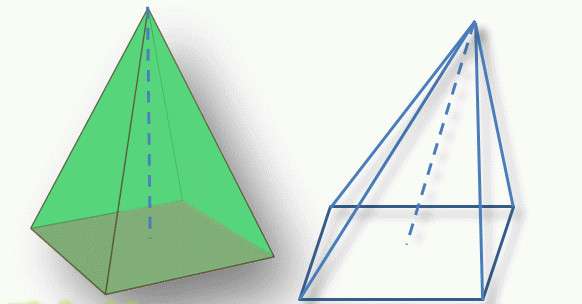
Важным моментом при определении типа фигуры является положение вершины пирамиды относительно ее основания. Перпендикулярный отрезок, проведенный из вершины к многоугольному основанию, называется высотой фигуры. Если этот отрезок пересекает основание в его геометрическом центре (для треугольника - это пересечение медиан, для четырехугольника - пересечение диагоналей), то фигура называется прямой. В противном случае говорят о наклонной пирамиде.
Если n-угольник основания будет правильным (равносторонний треугольник, квадрат и другие), а фигура является прямой, тогда ее называют правильной пирамидой.
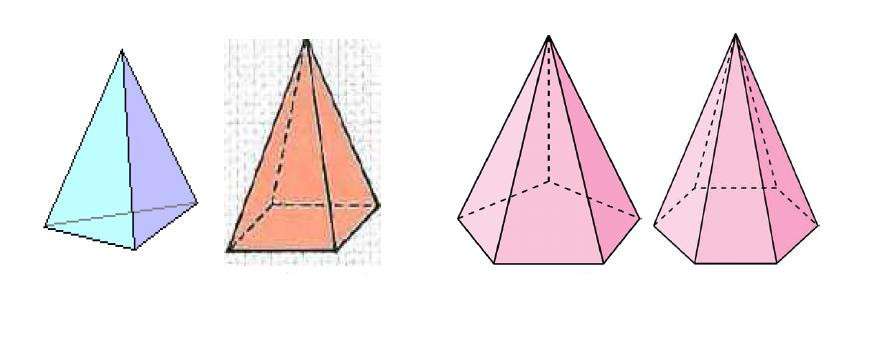
Рисунок выше показывает несколько пирамид, которые отличаются числом сторон многоугольника в основании.
Свойства правильных пирамид
Эти пирамиды от остальных фигур этого класса отличаются высокой степенью симметричности. В связи с этим с ними удобно проводить различные геометрические вычисления, например, объема или площади поверхности.
Правильная пирамида содержит в основании n-угольник, площадь которого однозначно определяется из знания длины его стороны. Боковая поверхность фигуры образована n одинаковыми треугольниками, которые являются равносторонними. Ребра правильной пирамиды, расположенные на боковой поверхности, равны друг другу. Значение длины этого ребра часто используют при расчете апотемы фигуры и определении площади поверхности.
Высота правильной пирамиды является второй важной характеристикой фигуры (первая - длина ребра основания). Высота используется при вычислении объема.
Всякая параллельная основанию плоскость, которая пересекает боковые грани пирамиды, приводит к образованию многоугольного сечения. Оно по отношению к многоугольнику основания является гомотетичным. Описанная операция среза приводит к образованию целого класса новых фигур - усеченных правильных пирамид.
Самые знаменитые пирамиды

Конечно же, таковыми являются правильные четырехугольные пирамиды египетских фараонов. В местечке под названием Гиза находятся более 100 этих каменных монументов, совершенство конструкции и точность геометрических параметров которых по сей день продолжают удивлять ученых. Самой большой из них является пирамида Хеопса, высота которой около 146 метров, а длина стороны около 230 метров.
Для чего конкретно служили эти пирамиды, а также при помощи каких механизмов и когда они были построены, никто не знает по настоящее время.
