Раздел физики, который изучает движение тел по различным траекториям, называется кинематикой. Практически полезными типами перемещения объектов являются движение по прямой и по окружности. Рассмотрим в статье, что представляют собой эти типы движения, какими формулами они описываются, а также приведем связь угловой и линейной скорости.
Движение по прямой
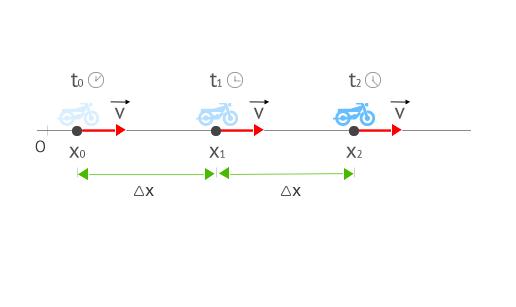
Связь угловой и линейной скорости можно определить, если знать, о каких величинах идет речь. Начнем со скорости линейной.
 Вам будет интересно:Манила, столица Филиппин: описание города, природные условия, фото
Вам будет интересно:Манила, столица Филиппин: описание города, природные условия, фото
Со школьной скамьи каждый знает, что перемещение объектов в пространстве характеризуется тремя главными величинами:
- пройденный путь S;
- время движения t;
- скорость v.
Формула, связывающая в единое равенство названные величины, приведена ниже:
S = v * t.
Приведенное выражение описывает равномерное движение тела по прямой линии. В международной системе единиц СИ величина S измеряется в метрах (м), t - в секундах (с), v - в метрах в секунду (м/с). Помимо названных единиц, путь и время могут измеряться в километрах (км) и часах (ч), соответственно. Тогда скорость будет выражаться в километрах в час (км/ч).
Записанная формула может применяться для решения широкого круга практических задач, например, движение транспортных средств по дорогам, движение кораблей и лодок по рекам, полет птиц и так далее.
Движение по окружности

Перед тем как перейти к выводу формулы связи линейной и угловой скорости, следует рассмотреть последнюю с точки зрения физики.
Угловая скорость появляется в физике, когда речь идет о вращающихся объектах. Примерами могут быть вращение колеса велосипеда, маховика автомобиля или планеты вокруг своей звезды. Угловая скорость тела показывает, на какой угол в радианах оно поворачивается за единицу времени. Обычно эту величину обозначают греческой буквой ω (омега). Она измеряется в радианах в секунду (рад/с).
По аналогии с линейным случаем можно назвать три главных величины, которые описывают движение по окружности с постоянной скоростью угловой:
- угол поворота θ;
- время t;
- угловая скорость ω.
Соответствующая формула, которая связывает эти величины, выглядит так:
θ = ω * t.
Угол поворота тела θ вокруг оси вращения измеряется в радианах. Напомним, что окружность имеет 2 * pi радиан (около 6,28). Если полученное по формуле значение θ оказалось больше, чем 2 * pi, то это означает, что тело сделало больше одного оборота вокруг оси.
Таким образом, записанное выражение позволяет рассчитать число оборотов, совершаемых телом за известный промежуток времени t.
Связь угловой и линейной скорости
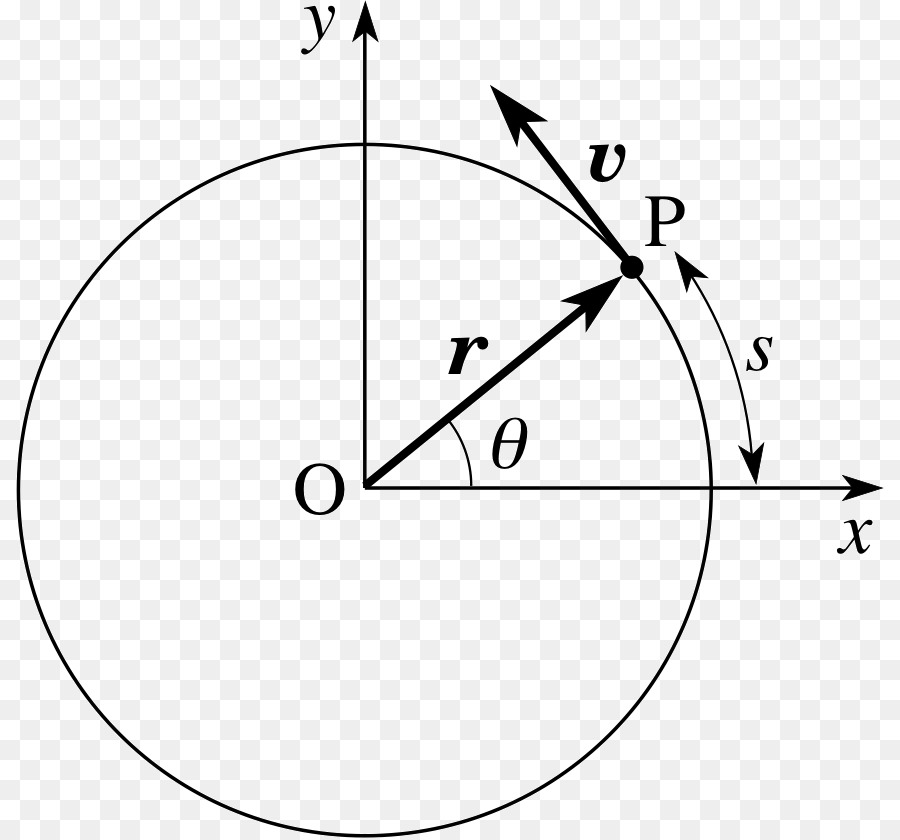
Теперь можно рассмотреть этот вопрос. Предположим, что тело, имеющее линейную скорость v, вращается по окружности радиусом R. Чтобы получить между линейной и угловой скоростью связь, рассмотрим, какое время понадобится телу, чтобы сделать полный один оборот. Поскольку пройденный путь будет равен длине окружности, то следующее выражение будет справедливым:
t = S/v = 2 * pi * R/v.
Теперь воспользуемся угловыми величинами. За найденное время одного оборота t, тело повернется точно на 2 * pi радиан. Последнее означает, что его угловая скорость будет равна:
ω = θ/t = 2 * pi/t.
Подставим рассчитанное выше время t и получим между угловой и линейной скоростью связь:
ω = 2 * pi/t = 2 * pi/(2 * pi * R/v) = v/R.
Полученную формулу можно записать в двух видах:
ω = v/R;
v = ω * R.
Каждое из выражений применяется в зависимости от того, какая величина в условии задачи известна. Формулы позволяют сделать важный вывод: чем больше радиус орбиты вращение, тем больше будет линейная скорость при постоянной угловой скорости.
Далее решим интересную задачу на применение полученных формул.
Что быстрее - Земля или Марс?
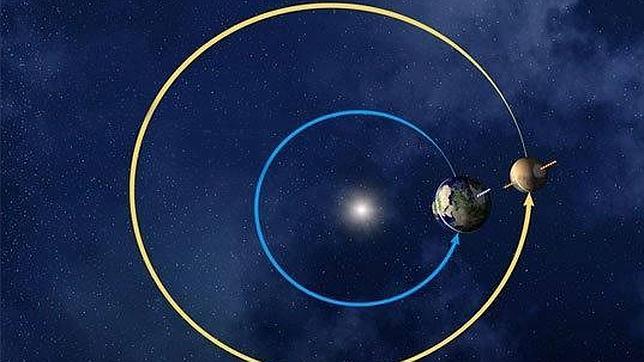
Известно, что Земля и Марс являются 3-й и 4-й планетами Солнечной системы, соответственно. Обе планеты движутся приблизительно по круглым орбитам. Расстояние от нашей звезды до Земли равно 149 597 870,691 км, а один оборот вокруг нее она делает за 365,256 дней. Марс расположен от Солнца на расстоянии 227 936 640 км, и один оборот вокруг него делает за 686,971 земных дня. Необходимо определить и сравнить линейные скорости планет.
Угловая скорость планеты может быть рассчитана по формуле:
ω = 2 * pi/T.
Где T - период (время совершения одного оборота вокруг звезды). Подставляя ω в формулу для v, получаем:
v = 2 * pi * R/T.
Переведем время оборота планет в часы и подставим данные в это равенство, получим:
- для Земли: v = 2 * 3,14 * 149597870,691/(365,256 * 24) ≈ 107,2 тыс. км/ч;
- для Марса: v = 2 * 3,14 * 227936640/(686,971 * 24) ≈ 86,8 тыс. км/ч.
Обе цифры являются огромными. Так, Земля за один час пролетает в космосе расстояние, практически равное трем ее окружностям по экватору. Полученные скорости свидетельствуют, что Земля движется быстрее Марса, и ее скорость на 24 % больше марсианской.
