Все виды движения, с которыми человек сталкивается на протяжении своей жизни, изучаются в физике в рамках законов классической механики Ньютона. В данной статье речь пойдет о вращении твердых тел, об уравнениях, которые его описывают, и о формулах углового ускорения.
Вращение в природе и технике
Прежде чем изучать угловое ускорение и формулы, которые позволяют его определить, рассмотрим, что представляет собой процесс вращения.
Вам будет интересно:Мотивация учебной деятельности младших школьников: понятие, основные принципы, цели, задачи и примеры
В физике под вращением понимают такой тип движения, при котором каждая точка тела произвольной формы или материальная точка движется по круговой траектории. Через центр этой траектории перпендикулярно ее плоскости проходит ось вращения. Рассматриваемый тип перемещения в пространстве может происходить с постоянной скоростью или с переменной. В последнем случае говорят о наличие у тела ускорения.
Вам будет интересно:Сокровища - это... Значение слова, фильмы с этим словом и не только
Примерами вращения в быту являются движение лопастей вентилятора, вращение колес велосипеда и автомобиля, вращение ножей блендера или рабочей части миксера, движение валов и шестерен. В природе также можно наблюдать этот тип движения, например, перемещение нашей Земли вокруг Солнца и ее суточное вращение вокруг своей оси.
Какими величинами описывают вращение?
Поскольку рассматриваемый вид движения происходит по круговой траектории, то оказывается удобным описать его с помощью величин, которые используют величину угла кругового сектора. Перечислим эти величины.
Угол θ - это центральный угол кругового сектора. Для наглядности он показан ниже на рисунке.
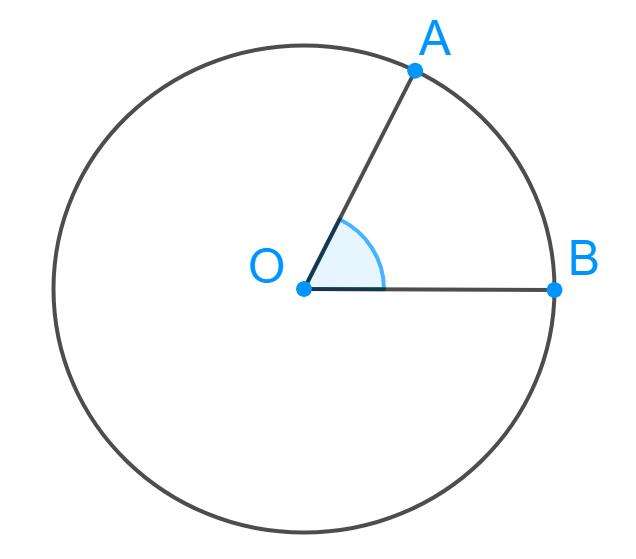
Здесь дуга AB - это расстояние, которое прошло вращающееся тело за некоторый промежуток времени t. Используя соответствующую пропорцию, можно получить связь между длиной этой дуги L и углом θ, выраженным в радианах. Эта связь имеет следующий математический вид:
L = θ × r
Символом r обозначен радиус окружности. Напомним, что один оборот по круговой траектории соответствует углу θ = 2 × pi.
Следующая важная кинематическая величина вращения - это скорость. Ее, как правило, обозначают греческой буквой ω (омега) и определяют в радианах в секунду. Отличие этой скорости, которая называется угловой, от ее линейного аналога является очевидным, поскольку последняя измеряется в метрах в секунду. Математически величина ω определяется так:
ω = dθ / dt
То есть угловая скорость показывает быстроту поворота тела. Записанное выражение называется мгновенной скоростью, вычисленной в бесконечно малый промежуток времени (t; t + dt). Формула для средней скорости ωm запишется в виде:
ωm = θ / t
При этом на угловом промежутке θ мгновенная скорость ω может значительно изменяться.
Наконец, третьей важной величиной, которая используется для описания неравномерного движения по окружности, является угловое ускорение α. Эта величина показывает как изменяется скорость на данном промежутке времени. Формула углового ускорения через скорость угловую выглядит следующим образом:
α = dω / dt
Отсюда следует, что единицей измерения α является радиан в квадратную секунду (рад/с2).
Динамика вращения и угловое ускорение
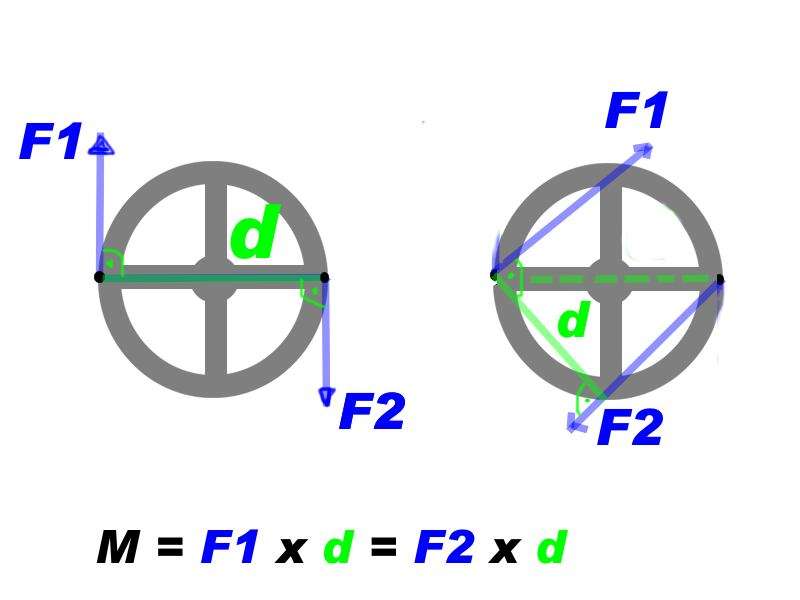
Вспоминая законы Ньютона для движения, можно сказать, что любое изменение в механическом перемещении твердого тела связано с действием некоторой внешней силы. В случае вращения рассматривают не саму силу, а ее момент. Последний равен векторному произведению силы на вектор расстояния от оси до точки приложения силы, то есть:
M¯ = [r¯ × F¯]
Этот момент приводит либо к торможению вращения, либо к его ускорению. В обоих случаях уравнение движения в скалярной форме записывается в виде:
M = I × α
Где I момент инерции (аналог массы тела для прямолинейного движения). Последнее равенство позволяет записать формулу для вычисления углового ускорения в динамике:
α = M / I.
Таким образом, зная моменты силы и инерции, можно рассчитать ускорения α.
Кинематика ускоренного вращения
Если скорость вращения в течение некоторого времени не изменяет своей величины, то говорить об угловом ускорении тела не приходится, поскольку оно равно нулю. Если же скорость изменяется с течением времени, то движение называется ускоренным. Для него справедлива формула:
ω = α × t
Это равенство справедливо только тогда, когда α не является функцией времени, то есть α = const. Такое движение называется равноускоренным.
Угол поворота для равноускоренного движения тела с места, то есть при отсутствии начальной скорости вращения, можно вычислить так:
θ = α × t2 / 2
Отсюда получаем формулу углового ускорения через центральный угол поворота:
α = (2 × θ) / t2
Отметим, если тело сначала вращалось без ускорения со скоростью ω0, а затем, начало двигаться ускоренно, то для пройденного им углового расстояния можно записать:
θ = ω0 × t + α × t2 / 2
Отсюда несложно получить соответствующее выражение для α.
Связь между линейным и угловым ускорением
Линейное ускорение a показывает прирост скорости v за время t. Эта величина измеряется в метрах в секунду квадратную, то есть:
a = dv / dt
Чтобы найти связь между величинами a и α обратимся к следующей формуле, приведенной ранее:
L = θ × r
Возьмем производную от левой и правой части равенства по времени, получим:
dL / dt = dθ / dt × r =>
v = ω × r
Возьмем еще раз производную по dt:
dv / dt = dω / dt × r =>
a = α × r
Мы получили формулу связи линейного и углового ускорений. Выражение показывает, что при постоянном ускорении α, величина a будет возрастать линейно с увеличением радиуса вращения.
Решение задачи
Известно, что автомобиль движется с линейным ускорением 2 м/с2. Необходимо определить угловое ускорение его колеса, если диаметр колеса равен 40 см.
Решение этой задачи можно выполнить, проведя последовательные математические выкладки, и переходя от линейных характеристик к угловым. Однако, выше было приведено равенство, связывающее величины a и α. Оно позволяет записать формулу углового ускорения колеса. Имеем:
a = α × r =>
α = 2 × a / d, где d = 2 × r.
Подставляем данные из условия, записываем ответ: α = 10 рад/с2.