Каждый из нас бросал камни в небо и наблюдал за траекторией их падения. Это самый распространенный пример движения твердого тела в поле гравитационных сил нашей планеты. В данной статье рассмотрим формулы, которые могут пригодиться для решения задач на свободное движение тела, брошенного к горизонту под углом.
Понятие о движении к горизонту под углом
Когда некоторому твердому объекту сообщают начальную скорость, и он начинает набирать высоту, а затем, снова падать на землю, то принято считать, что тело движется по параболической траектории. На самом деле решение уравнений для этого типа движения показывает, что описываемая телом линия в воздухе - это часть эллипса. Однако для практического использования параболическая аппроксимация оказывается достаточно удобной и приводит к точным результатам.
Вам будет интересно:Явление фотоэффекта. Красная граница фотоэффекта. Пример решения задачи
Примерами движения тела, брошенного под углом к горизонту, является выстрел снаряда из дула пушки, удар ногой по мячу, и даже прыжки гальки на поверхности воды ("жабки"), по которым проводятся международные соревнования.
Тип движения под углом изучает баллистика.
Свойства рассматриваемого типа движения
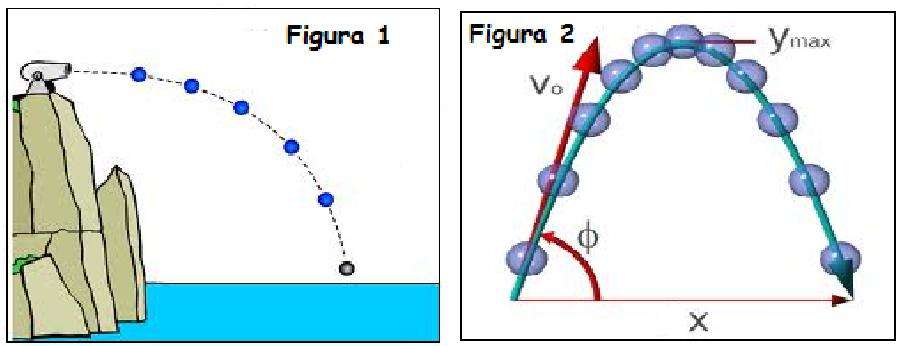
Когда рассматривают траекторию движения тела в поле гравитационных сил Земли, то оказываются справедливыми следующие утверждения:
- знание начальной высоты, скорости и угла к горизонту позволяет рассчитать всю траекторию;
- угол вылета равен углу падения тела при условии, что начальная высота равна нулю;
- движение по вертикали можно рассматривать независимо от движения по горизонтали;
Отметим, что указанные свойства справедливы, если сила трения в процессе полета тела пренебрежимо мала. В баллистике при изучении полетов снарядов учитывают много разных факторов, в том числе и трение.
Типы параболического движения
В зависимости от того, с какой высоты начинается движение, на какой высоте заканчивается, и как направлена начальная скорость, выделяют следующие типы параболического движения:
- Полная парабола. В этом случае тело бросают с поверхности земли, и на эту поверхность оно падает, описав при этом полную параболу.
- Половина параболы. Такой график движения тела наблюдается, если его бросить с некоторой высоты h, направив скорость v параллельно горизонту, то есть под углом θ = 0o.
- Часть параболы. Такие траектории возникают, когда тело брошено под некоторым углом θ≠0o, и разница начальной и конечной высоты тоже не равна нулю (h-h0≠0). Большинство траекторий движения объектов относятся именно к этому типу. Например, выстрел с пушки, стоящей на холме, или бросок баскетболистом мяча в корзину.
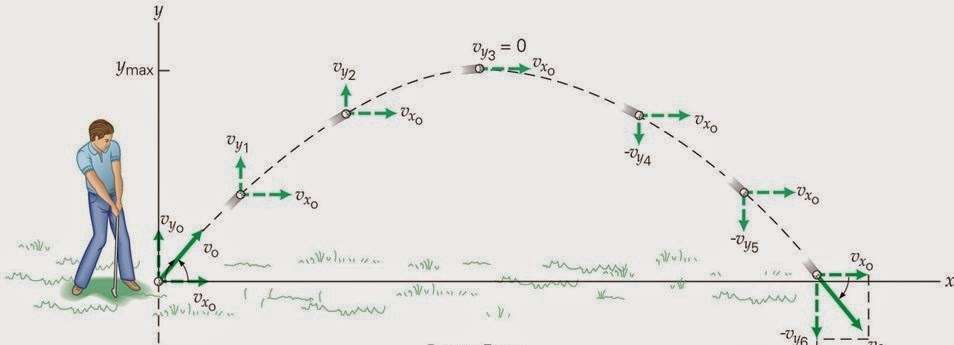
График движения тела, соответствующий полной параболе, приведен выше.
Необходимые для расчета формулы
Приведем формулы для описания движения тела, брошенного под углом к горизонту. Пренебрегая силой трения, и учитывая только силу тяжести, можно записать два уравнения для скорости перемещения объекта:
vx = v0*cos(θ)
vy = v0*sin(θ) - g*t
Так как сила тяжести направлена вертикально вниз, то горизонтальную компоненту скорости vx она не изменяет, поэтому в первом равенстве отсутствует зависимость от времени. Компонента vy в свою очередь испытывает влияние силы тяжести, которая сообщает g ускорение телу, направленное к земле (отсюда знак минус в формуле).
Теперь запишем формулы для изменения координат тела, брошенного под углом к горизонту:
x = x0+v0*cos(θ)*t
y = y0 + v0*sin(θ)*t - g*t2/2
Начальная координата x0 часто принимается равной нулю. Координата y0 - это не что иное, как высота h, с которой бросают тело (y0 = h).
Теперь выразим время t из первого выражения и подставим его во второе, получим:
y = h + tg(θ)*x - g /(2*v02*cos2(θ))*x2
Это выражение в геометрии соответствует параболе, ветви которой направлены вниз.
Приведенных уравнений достаточно, чтобы определить любые характеристики этого типа движения. Так, их решение приводит к тому, что максимальная дальность полета достигается, если θ = 45o, максимальная же высота, на которую поднимется брошенное тело, достигается при θ = 90o.
