Вопрос перемещения тел в пространстве является объектом изучения кинематики. С точки зрения этого раздела физики, рассмотрим в данной статье специальный вид перемещения - равноускоренное движение. Определение и формулы будут приведены далее.
Траектория, путь, скорость и ускорение
Прежде чем рассматривать определение равноускоренного движения, следует ввести главные характеристики и понятия, которые используются в кинематике для описания механического перемещения тел. В названии пункта приведены эти понятия. Опишем каждое из них подробнее.
 Вам будет интересно:Слово "тятя" - это устаревшее "папа"
Вам будет интересно:Слово "тятя" - это устаревшее "папа"
Траектория движения является воображаемой, несуществующей линией пространства, вдоль которой тело осуществляет движение. Самыми простыми случаями являются прямолинейные и круговые траектории, которые часто встречаются в природе и технике. Например, автомобиль, движущийся по дороге, осуществляет прямолинейное движение. Однако тот же автомобиль, совершающий затяжной поворот, перемещается по круговой траектории некоторого радиуса.
Путь (обозначим его буквой L) - это расстояние, измеряемое в единицах длины, которое тело проходит за рассматриваемый промежуток времени. В случае вращения вместо линейного пути используют его угловой аналог - центральный угол поворота в радианах (обозначим его θ).
 Вам будет интересно:Агитировать — это пытаться убедить
Вам будет интересно:Агитировать — это пытаться убедить
Скорость - это векторная характеристика движения, отражающая быстроту изменения пространственных координат. Мгновенная скорость, то есть скорость в данный момент времени, вычисляется по формуле:
- v¯ = dL/dt.
Измеряется эта величина в метрах в секунду в СИ и направлена всегда по касательной к траектории.
Ускорение - одна из важных величин кинематики. Оно определяет быстроту изменения скорости. Здесь под изменением понимают не только абсолютное значение величины v¯, но и ее направление. Согласно этому определению можно записать следующее выражение для ускорения:
- a¯ = dv¯/dt.
Вектор ускорения не совпадает с вектором скорости в общем случае. Он направлен в сторону действующей на тело силы, поэтому со скоростью ничего общего не имеет.
Приведенное ниже определение равноускоренного движения связано с особенностью поведения функции a¯(t).
Полное ускорение и компоненты его разложения
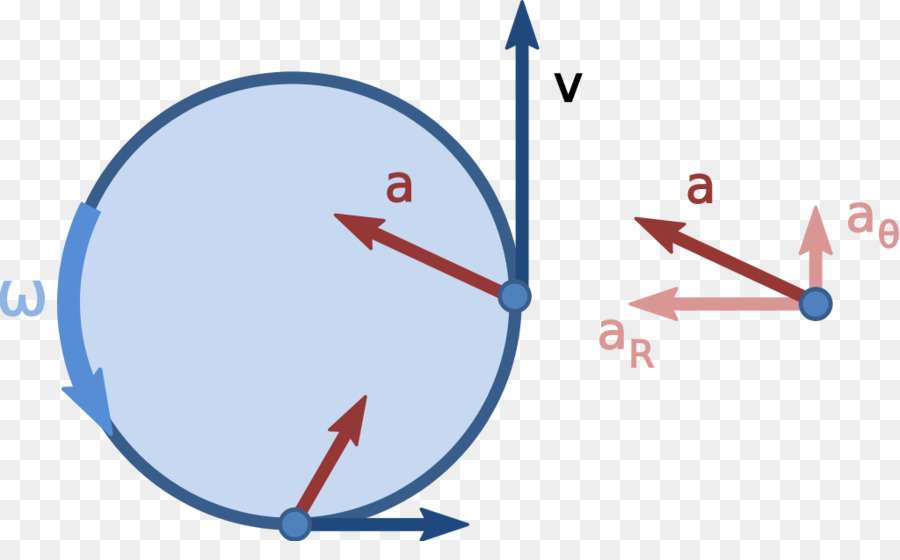
Форма траектории перемещения тел является ключевым вопросом в понимании определения равноускоренного движения. Дело в том, что любая криволинейная траектория предполагает наличие у величины ускорения a¯ двух ненулевых компонент. Они называются касательной и нормальной компонентами ускорения. Первая определяет изменение скорости по модулю (at), вторая определяет изменение скорости по направлению (ac). Обе компоненты взаимно перпендикулярны друг другу, поэтому через их модули полное ускорение можно вычислить так:
- a = √(ac2+at2).
Важно запомнить, что нормальное ускорение ac (его также называют центростремительным) появляется только в случае криволинейной траектории. Это ускорение от изменения модуля скорости не зависит.
Движение с постоянным ускорением
Название данного раздела является определением равноускоренного движения. Иными словами, движение будет равноускоренным только тогда, когда ускорение является постоянной величиной и не зависит от времени. О каком ускорении идет речь? Конечно же, о касательной составляющей ускорения.
Чтобы объяснить, почему независимость от времени полного ускорения не гарантирует, что движение является равноускоренным, приведем простой пример. Предположим, что тело равномерно вращается по окружности, например наша Земля - вокруг Солнца. Модуль скорости сохраняется в любой точке траектории, а это означает, что касательное ускорение равно нулю, то есть движение является равномерным. Полное же ускорение нулю не равно, поскольку нормальная его составляющая имеет некоторое постоянное конечное значение.
В случае движения по прямой линии касательное и полное ускорения равны друг другу. Этот факт позволяет вести речь о полном ускорении при исследовании равноускоренного движения по прямой линии.
Чистое равноускоренное движение по прямой
Под словом "чистое" имеется в виду, что при рассмотрении этого движения не существует начальной скорости. Тело из состояния покоя сразу начинает двигаться равноускоренно. В этом случае полное ускорение постоянно. Для скорости можно записать формулу:
- v = a×t.
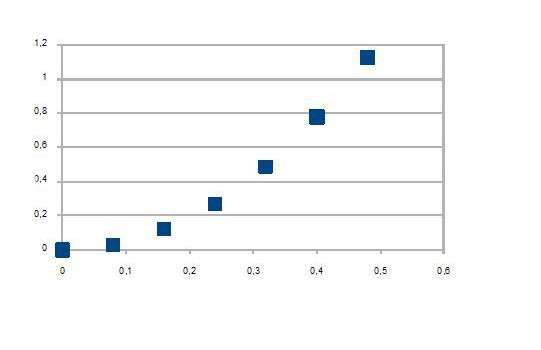
Графиком этого равенства является прямая, проходящая через точку (v = 0; t = 0). Тангенс угла наклона прямой к оси x равен численно величине ускорения a.
Проинтегрировав записанное выражение по времени, получаем формулу перемещения тела при равноускоренном движении:
- L = a*t2/2.
Графиком пути L от времени является правая ветвь параболы, которая начинается в точке (0; 0).
Движение с постоянным ускорением и с начальной скоростью
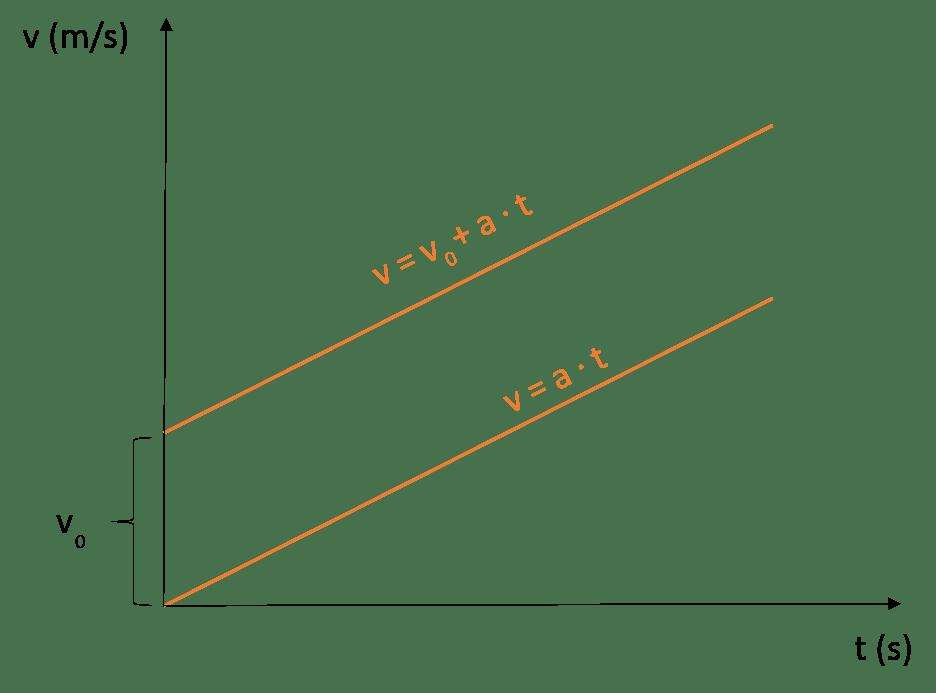
Выше был рассмотрен вопрос равноускоренного движения без начальной скорости. Теперь предположим, что тело начало движение и некоторое время перемещалось со скоростью v0. Затем в результате действия внешней силы оно начало ускоряться с постоянным ускорением a. В этом случае формула для скорости примет вид:
- v = v0 + a × t.
Как и в предыдущем случае, графиком функции v(t) также является прямая, только теперь она начинается в точке (v0; 0). Отметим, что отчет времени t начинают вести в момент появления ускорения. Так, если подставить в формулу значение t = 0, то мы получим начальную скорость.
Взяв интеграл по времени от функции v(t), получаем соответствующее выражение для пути:
- L = v0 × t + a × t2/2.
Графиком функции L(t) является парабола, как и в случае чистого движения с ускорением. Эта парабола также проходит через начало координат. Единственным и важным ее отличием является то, что ветвь этой параболы лежит ближе к оси y, чем предыдущий график (при условии, что значения ускорений a в обоих случаях равны).
Свободное падение в гравитационном поле
Мы привели определение равноускоренного движения и рассмотрели формулы кинематики, с помощью которых оно описывается. Теперь приведем самый известный в природе пример этого вида перемещения - свободное падение.
На любое тело, имеющее массу и находящееся вблизи поверхности земли, действует сила гравитационного притяжения нашей планеты. Эта сила прямо пропорциональна массе, где роль коэффициента пропорциональности играет ускорение свободного падения. Его принято обозначать буквой g. Оно равно приблизительно 9,81 м/с2, то есть за каждую секунду падения тело увеличивает свою скорость почти на 10 м/с.
Ускорение g является "визитной карточкой" каждой планеты и зависит от радиуса и массы последней. Так, на Луне g = 1,62 м/с2, а на Юпитере оно составляет 24,79 м/с2.
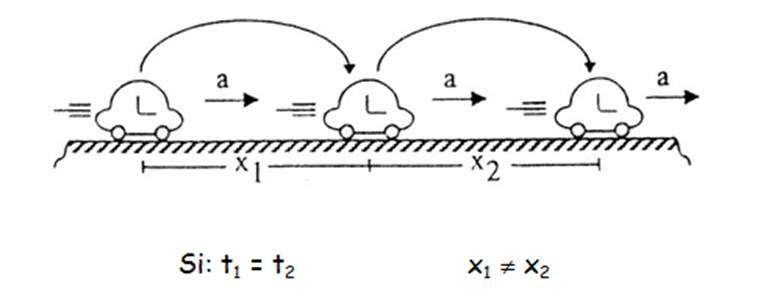
Задача с движущимся автомобилем
Начиная равноускоренное движение, автомобиль двигался некоторое время. За это время он проехал расстояние 250 метров. Полагая, что ускорение постоянно и равно 2 м/с2, необходимо определить время движения транспортного средства.

Данная задача решается с использованием формулы для чистого равноускоренного движения. Запишем ее:
- L = a × t2/2.
Выражаем отсюда время t, получаем:
- t = √(2 × L/a).
Данные из условия приводят к ответу: t = 15,8 секунды.