Механическое движение окружает нас с самого рождения. Каждый день мы видим, как движутся по дорогам машины, по морям и рекам корабли, летают самолеты, даже наша планета движется, пересекая космическое пространство. Важной характеристикой для всех без исключения видов движения является ускорение. Это физическая величина, типы и основные характеристики которой будут рассмотрены в данной статье.
Физическое понятие об ускорении
 Вам будет интересно:Что такое криминология: задачи и цели
Вам будет интересно:Что такое криминология: задачи и цели
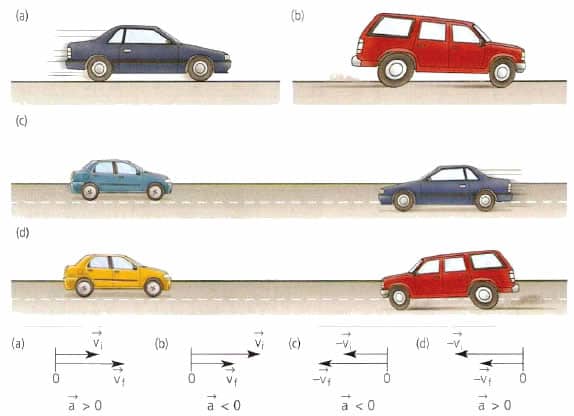
Многим термин "ускорение" интуитивно знаком. В физике ускорение - это величина, характеризующая любое изменение во времени скорости. Соответствующая математическая формулировка имеет вид:
a¯ = dv¯/ dt
Черта над символом в формуле означает, что эта величина векторная. Таким образом, ускорение a¯ является вектором и описывает оно изменение также векторной величины — скорости v¯. Это ускорение называется полным, оно измеряется в метрах в секунду квадратную. Например, если тело увеличивает за каждую секунду своего движения скорость на 1 м/с, то соответствующее ускорение равно 1 м/с2.
Откуда возникает ускорение и куда оно направлено?
Мы разобрались с определением, что это ускорение. Также было выяснено, что речь идет о величине векторной. Куда направлен этот вектор?
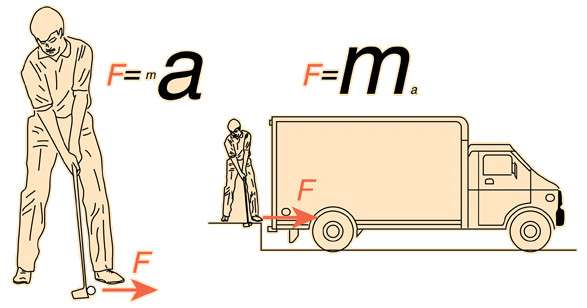
Чтобы дать правильный ответ на поставленный выше вопрос, следует вспомнить второй закон Ньютона. В общепринятой форме он записывается следующим образом:
F¯ = m*a¯
Словами можно прочитать это равенство так: действующая на тело массой m сила F¯ любой природы приводит к появлению у этого тела ускорения a¯. Поскольку масса — это скалярная величина, то получается, что вектора силы и ускорения будут направленными вдоль одной и той же прямой. Иными словами, ускорение всегда направлено в сторону действия силы и совершенно не зависит от вектора скорости v¯. Последний направлен вдоль касательной к траектории движения.
Криволинейное движение и компоненты полного ускорения
В природе мы часто встречаемся с движением тел по криволинейным траекториям. Рассмотрим, как можно описать ускорение в этом случае. Для этого предположим, что скорость материальной точки в рассматриваемой части траектории может быть записана в виде:
v¯ = v*ut¯
Скорость v¯ является произведением его абсолютной величины v на единичный вектор ut¯, направленный вдоль касательной к траектории (тангенциальная составляющая).
Согласно определению, ускорение — это производная скорости по времени. Имеем:
a¯ = dv¯/dt = d(v*ut¯)/dt = dv/dt*ut¯ + v*d(ut¯)/dt
Первое слагаемое в правой части записанного равенства называется тангенциальным ускорением. Так же, как и скорость, оно направлено вдоль касательной и характеризует изменение абсолютной величины v¯. Второе слагаемое — это ускорение нормальное (центростремительное), оно направлено перпендикулярно к касательной и характеризует изменение вектора величины v¯.
Таким образом, если радиус кривизны траектории равен бесконечности (прямая линия), то вектор скорости в процессе перемещения тела не меняет своего направления. Последнее означает, что нормальная составляющая полного ускорения равна нулю.
В случае движения материальной точки по окружности равномерно, модуль скорости остается постоянным, то есть тангенциальная компонента полного ускорения равна нулю. Нормальная же составляющая направлена к центру окружности и вычисляется по формуле:
an = v2/r
Здесь r — радиус. Причиной появления центростремительного ускорения является действие на тело некоторой внутренней силы, которая направлена к центру окружности. Например, для движения планет вокруг Солнца этой силой является гравитационное притяжение.
Формула, которая связывает модули полного ускорения и его компонент at (касательная), an (нормальная), имеет вид:
a = √(at2 + an2)
Равноускоренное перемещение по прямой линии
Движение по прямой с постоянным ускорением часто встречается в быту, например это перемещение автомобиля по дороге. Этот вид движения описывается следующим уравнением для скорости:
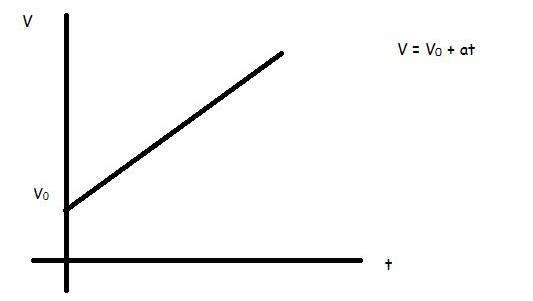
v = v0 + a*t
Здесь v0 — некоторая скорость, которой тело обладало до возникновения у него ускорения a.
Если изобразить график функции v(t), то мы получим прямую линию, которая ось y пересекает в точке с координатами (0; v0), а тангенс угла наклона к оси x равен модулю ускорения a.
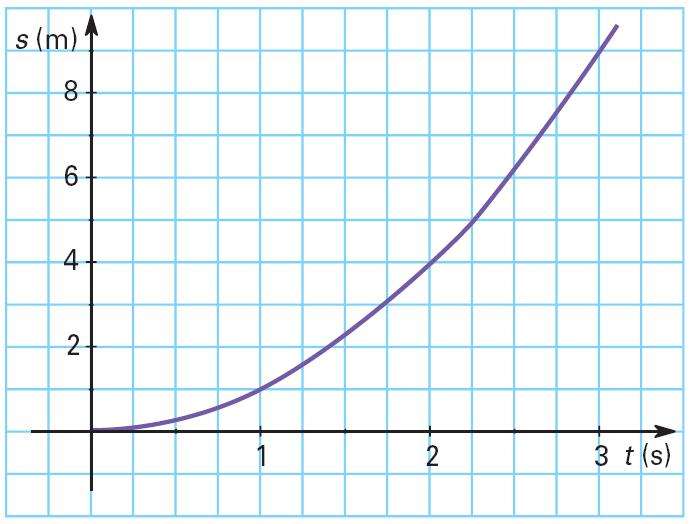
Взяв интеграл от функции v(t), мы получим формулу для пути L:
L = v0*t + a*t2/2
График функции L(t) - это правая ветвь параболы, которая начинается в точке (0; 0).
Приведенные формулы являются основными уравнениями кинематики ускоренного перемещения по прямой.
Если тело, имея начальную скорость v0, начинает замедлять свое движение с ускорением постоянным, то говорят о равнозамедленном перемещении. Для него справедливы следующие формулы:
v = v0 - a*t;
L = v0*t - a*t2/2
Решение задачи на вычисление ускорения
Находясь в неподвижном состоянии, автомобиль начинает движение. При этом за 20 первых секунд он проходит расстояние 200 метров. Чему равно ускорение автомобиля?
Сначала запишем общее кинематическое уравнение для пути L:
L = v0*t + a*t2/2
Поскольку в нашем случае транспортное средство находилось в состоянии покоя, то его скорость v0 была равна нулю. Получаем формулу для ускорения:
L = a*t2/2 =>
a = 2*L/t2
Подставляем значение пройденного пути L = 200 м за промежуток времени t = 20 с и записываем ответ на вопрос задачи: a = 1 м/с2.
