Движение с ускорением различных объектов окружает нас каждый день. Достаточно лишь вспомнить автомобили, самолеты, велосипеды, вращающиеся колеса и валы, чтобы понять всю важность ускоренного перемещения тел в жизни человека. Для описания этого движения в физике существует специальный раздел, он называется кинематикой. В данной статье рассмотрим, какими формулами описывается перемещение при равноускоренном движении.
Понятие об ускорении, скорости и пути
 Вам будет интересно:«Тлетворный» — это о разложении
Вам будет интересно:«Тлетворный» — это о разложении
Прежде чем записывать формулы перемещения при равноускоренном движении, следует дать понятие основным величинам, которые в них фигурируют.
Начнем с пути. Под этой величиной понимают расстояние, которое проходит тело за интервал времени, двигаясь по известной траектории. Чем за более короткое время тело проходит некоторый путь L, тем больше его скорость. Таким образом, скоростью тела является быстрота преодоления им расстояний в пространстве. В данный момент времени расчет скорости выполняют по такой формуле:
v¯ = dL/dt
Скорость - это вектор, а путь - скаляр. Скорость направлена вдоль касательной, восстановленной к данной точке траектории.
Если наблюдать за телом, движущимся вдоль траектории некоторое время, и в каждой точке траектории измерять его скорость, то окажется, что она постоянно меняется. Изменение скорости характеризуют ускорением. В соответствии с определением ускорения оно вычисляется так:
a¯ = dv¯/dt
Ускорение также является величиной векторной, только с направлением скорости оно не имеет ничего общего. Вектор ускорения повернут в сторону изменения скорости за данное время или, что одно и то же, в сторону действующей на тело силы.
Равноускоренное движение в физике
Чтобы понять, что такое равноускоренное перемещение, приведем следующий пример: предположим, что автомобиль находился в покое. Затем он начал движение, постоянно увеличивая свою скорость. Если за равные промежутки времени прирост модуля скорости автомобиля был одинаковым, то можно говорить о равноускоренном движении тела. Иными словами, во время рассматриваемого вида перемещения ускорение является величиной постоянной (a = const).

Не стоит думать, что движение с постоянным ускорением может только увеличивать скорость. В результате такого перемещения скорость тела может также уменьшаться до полной его остановки. Такая ситуация возникает, когда транспортное средство осуществляет процесс торможения. В этом случае ускорение будет направлено против вектора скорости.
В природе распространенным движением с постоянным ускорением является падение тел. До определенных скоростей, когда сопротивлением воздуха можно пренебречь, свободное падения является равноускоренным, причем величина ускорения равна 9,81 м/с2.
Изменение скорости при движении с постоянным ускорением
В отличие от ускорения, скорость при равноускоренном движении постоянной величиной не является. Рассмотрим для простоты перемещение по прямой линии. В случае если вектора величин a¯ и v¯ совпадают, имеет место следующая формула для скорости:
v = v0 + a*t
Это выражение предполагает, что до появления ускорения тело уже обладало некоторой скоростью v0.
Данная формула показывает, что скорость линейно возрастает с течением времени. График функции v(t) представляет собой прямую линию, которая пересекает ось y на расстоянии v0 от начала координат.
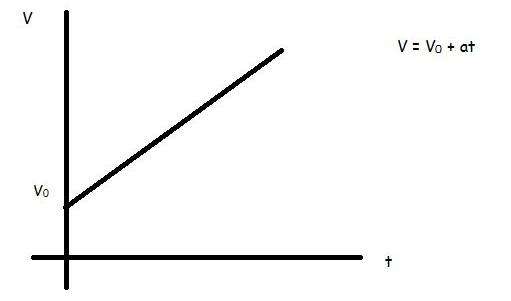
При равноускоренном движении скорость также может уменьшаться линейно. Для этого необходимо, чтобы вектора ускорения и скорости были противоположными (торможение автомобиля, свободный взлет тела в высоту). Для этого случая можно записать такое выражение:
v = v0 - a*t
Как и в предыдущем случае, графиком равенства является прямая, только коэффициент ее наклона к оси x будет не положительным, а отрицательным.
Перемещение при равноускоренном движении
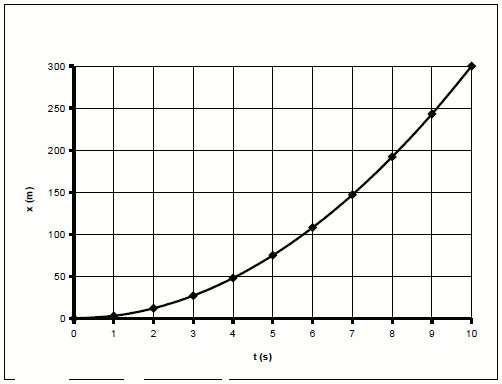
Формула пути однозначно получается, если взять интеграл по времени от скорости. В случае когда скорость тела увеличивается, для пути можно записать следующее выражение:
L = v0*t + a*t2/2
Видно, что графиком функции L(t) является парабола (ее правая ветвь). То есть пройденный путь с течением времени быстро увеличивается.
Если ускорение приводит к уменьшению скорости, тогда формула перемещения при равноускоренном движении примет вид:
L = v0*t - a*t2/2
Графиком для этого уравнения тоже будет парабола, однако ее ветвь постепенно приближается к некоторому постоянному значению. Последнее соответствует пройденному пути до остановки движущегося тела.
Движение с постоянным ускорением по окружности
Чтобы полнее охарактеризовать тему, следует также привести формулы перемещения при равноускоренном движении по окружности. В отличие от прямолинейного движения, этот вид перемещения описывается угловыми величинами. Тем не менее угловые величины являются полными аналогами соответствующих линейных характеристик.
Для скорости при равноускоренном движении вращения справедлива формула:
ω = ω0 + α*t
Здесь ω - скорость угловая, которая измеряется в радианах в секунду (рад/с), α - ускорение угловое, оно измеряется в рад/с2.
Аналогом пути для вращения является угол поворота θ. Для него справедлива формула:
θ = ω0*t + α*t2/2
Таким образом, при равноускоренном вращении формулы кинематики сохраняют свой вид, но в них стоят уже угловые физические величины.
