Динамика вращения является одним из важных разделов физики. Она описывает причины движения тел по окружности вокруг некоторой оси. Одной из важных величин динамики вращения является момент силы, или вращающий момент. Что это - момент силы? Рассмотрим это понятие в данной статье.
Что следует знать о вращении тел?
Прежде чем давать ответ на вопрос, что это - момент силы, охарактеризуем с точки зрения физической геометрии процесс вращения.
Каждый человек интуитивно представляет, о чем идет речь. Вращение подразумевает под собой такое движение тела в пространстве, когда все его точки движутся по круговым траекториям вокруг некоторой оси или точки.
 Вам будет интересно:Магнитные свойства материала: основные характеристики и применение
Вам будет интересно:Магнитные свойства материала: основные характеристики и применение
В отличие от линейного перемещения, процесс вращения описывается угловыми физическими характеристиками. Среди них следует назвать угол поворота θ, угловую скорость ω и угловое ускорение α. Величина θ измеряется в радианах (рад), ω - в рад/с, α - в рад/с2.
Примерами вращения являются движение нашей планеты вокруг своей звезды, раскручивание ротора двигателя, движение колеса обозрения и другие.
Понятие о вращающем моменте
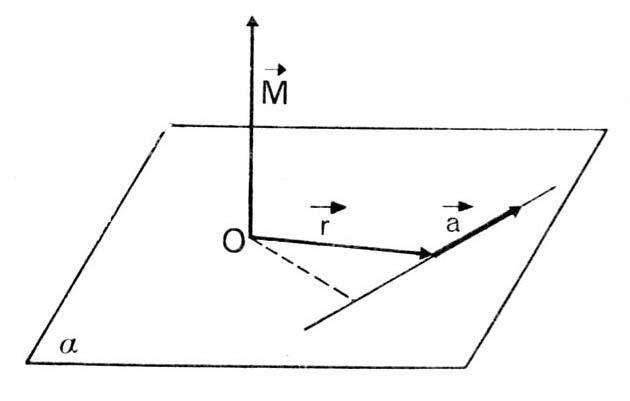
Момент силы - это физическая величина, равная векторному произведению радиус-вектора r¯, направленного от оси вращения к точке приложения силы F¯, и вектора этой силы. Математически это записывают так:
M¯ = [r¯ * F¯].
Как видно, момент силы - это величина векторная. Ее направление определяют по правилу буравчика или правой руки. Величина M¯ направлена перпендикулярно плоскости вращения.
На практике часто возникает необходимость вычисления абсолютного значения момента M¯. Для этого используют такое выражение:
M = r * F * sin(φ).
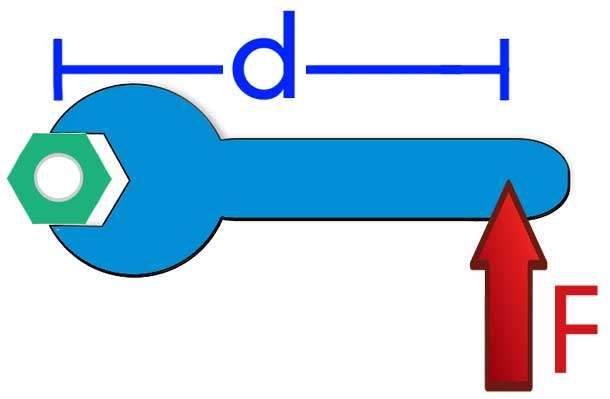
Где φ является углом между векторами r¯ и F¯. Произведение модуля радиус-вектора r на синус отмеченного угла называется плечом силы d. Последнее представляет собой расстояние между вектором F¯ и осью вращения. Формулу выше можно переписать в виде:
M = d * F, где d = r * sin(φ).
Момент силы измеряется в ньютонах на метр (Н*м). Тем не менее не следует прибегать к использованию джоулей (1 Н*м = 1 Дж), поскольку величина M¯ является не скаляром, а вектором.
Физический смысл величины M¯
Физическое значение момента силы проще всего понять на следующих примерах:
- Предлагаем проделать следующий эксперимент: постараться открыть дверь, толкнув ее вблизи петель. Чтобы проделать эту операцию с успехом, придется приложить большую силу. В то же время за ручку любая дверь открывается достаточно легко. Разница между двумя описанными случаями заключается в длине плеча силы (в первом случае она очень мала, поэтому и создаваемый момент будет небольшим и требует приложения большой силы).
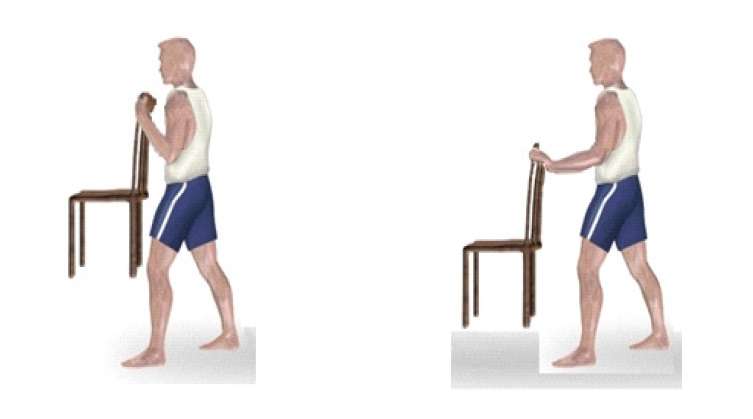
- Еще один эксперимент, показывающий смысл вращающего момента, заключается в следующем: возьмите стул и постарайтесь удержать его на вытянутой вперед руке на весу. Сделать это достаточно сложно. В то же время если прижать руку со стулом к телу, то задача уже не будет казаться непосильной.
- Каждый человек, связанный с техникой, знает, что открутить гаечным ключом гайку гораздо легче, чем делать это пальцами рук.
Все эти примеры говорят об одном: момент силы отражает способность последней совершить поворот системы вокруг оси. Чем больше вращающий момент, тем выше вероятность, что он выполнит поворот в системе и придаст ей угловое ускорение.
Вращающий момент и равновесие тел
Статика - раздел, занимающийся изучением причин равновесия тел. Если в рассматриваемой системе имеется одна или несколько осей вращения, значит, эта система потенциально может совершать круговое движение. Чтобы этого не происходило и система находилась в состоянии покоя, сумма всех n внешних моментов сил относительно любой оси должна равняться нулю, то есть:
∑i=1nMi = 0.
При использовании этого условия равновесия тел во время решения практических задач следует запомнить, что любая сила, стремящаяся повернуть систему против часовой стрелки, создает положительный вращающий момент, и наоборот.
Очевидно, что если сила приложена к оси вращения, то никакого момента она не создаст (плечо d равно нулю). Поэтому сила реакции опоры никогда не создает момента силы, если его рассчитывать относительно этой опоры.
Пример задачи
Разобравшись, как определить момент силы, решим следующую интересную физическую задачу: предположим, что имеется стол на двух опорах. Длина стола равна 1,5 метра, его масса составляет 30 кг. Груз массой 5 кг положили на расстоянии 1/3 от правого края стола. Необходимо рассчитать, какая сила реакции будет действовать на каждую опору стола с грузом.
Расчет задачи следует проводить в два этапа. На первом рассмотрим стол без груза. На него действуют три силы: две одинаковые реакции опоры и вес тела. Поскольку стол является симметричным, то реакции опор равны друг другу и вместе уравновешивают вес. Значение каждой реакции опоры составляет:
N0 = P / 2 = m * g / 2 = 30 * 9,81 / 2 = 147,15 Н.
Как только кладут груз на стол, то значения реакций опор изменяются. Чтобы их рассчитать, воспользуемся равновесием моментов. Сначала рассмотрим моменты сил, действующие относительно левой опоры стола. Этих моментов два: дополнительная реакция правой опоры без учета веса стола и вес самого груза. Поскольку система находится в равновесии, получаем:
ΔN1 * l - m1 * g * 2 / 3 * l = 0.
Здесь l - длина стола, m1 - масса груза. Из выражения получаем:
ΔN1 = m1 * g * 2 / 3 = 2 / 3 * 9,81 * 5 = 32,7 Н.
Аналогичным способом рассчитаем дополнительную реакцию на левую опору стола. Получаем:
-ΔN2 * l + m1 * g * 1/3 * l = 0;
ΔN2 = m1 * g * 1 / 3 = 1 / 3 * 5 * 9,81 = 16,35 Н.
Чтобы рассчитать реакции опор стола с грузом, необходимо величины ΔN1 и ΔN2 добавить к N0, получаем:
правая опора: N1 = N0 + ΔN1 = 147,15 + 32,7 = 179,85 Н;
левая опора: N2 = N0 + ΔN2 = 147,15 + 16,35 = 163,50 Н.
Таким образом, нагрузка на правую опору стола будет больше, чем на левую.