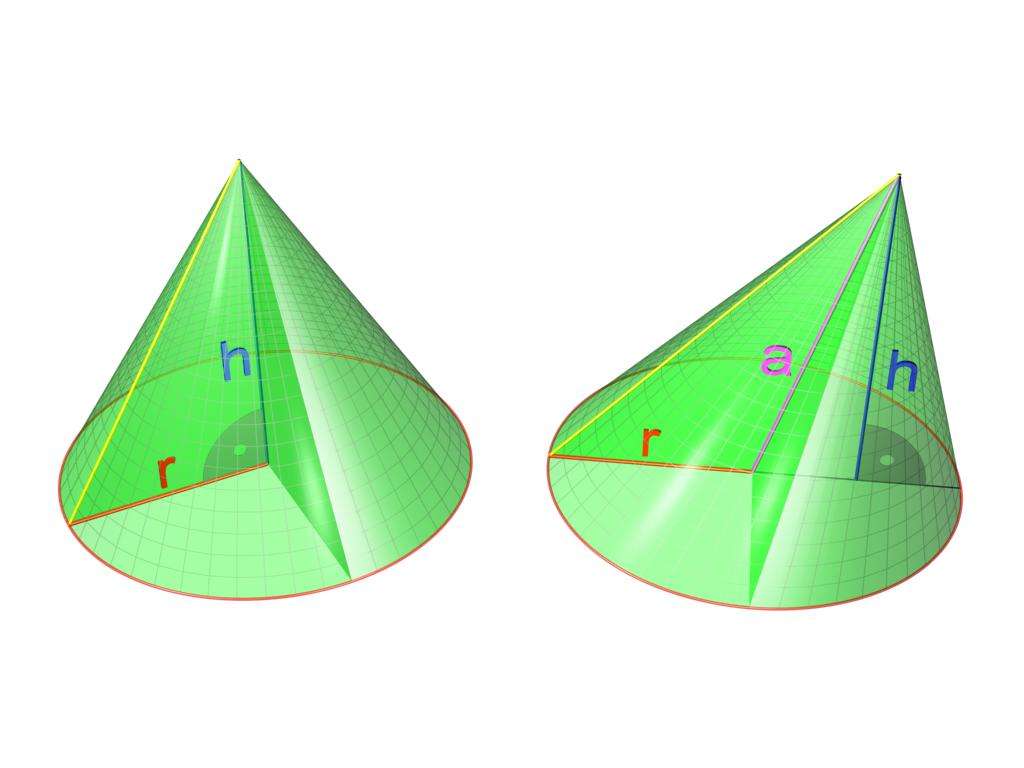
В курсе стереометрии общеобразовательных школ изучают несколько фигур вращения в трехмерном пространстве. Одной из них является конус. В данной статье подробно рассматривается вопрос, как найти объем конуса через площадь основания фигуры.
Что собой представляет конус?
Прежде чем приводить формулу объема конуса через основания площадь, дадим определение этой фигуре. Под конической поверхностью в стереометрии понимают такую поверхность, которая образована движение прямого отрезка, зафиксированного одним концом в некоторой точке, вдоль известной плоской кривой. Под плоской кривой, которая называется директрисой, имеется в виду любая кривая линия, лежащая в одной плоскости. Отрезок, который описывает поверхность, называется генератрисой.
 Вам будет интересно:Правило рычага. Формулировка и формула
Вам будет интересно:Правило рычага. Формулировка и формула
Сама по себе коническая поверхность объемом не обладает. Однако если директриса является замкнутой кривой, то она определяет плоскую фигуру, которая ограничивает коническую поверхность снизу. Совокупность конической поверхности и фигуры, ограниченной директрисой (основание), образуют конус. Он уже обладает некоторым объемом в пространстве.
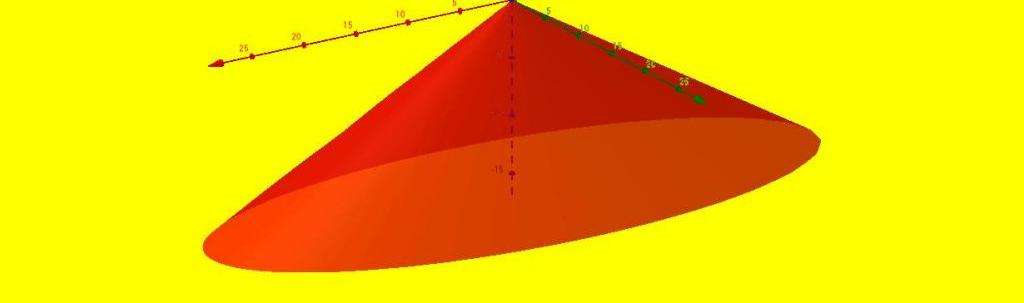
Фигура основания может иметь произвольный вид. Самыми распространенными являются эллипс и круг. Соответствующие конусы называются эллиптическим и круговым. Первый из них показан выше.
Формула объема конуса общего вида
Как найти объем конуса? Очень просто, достаточно знать лишь его высоту и площадь основания. Высота представляет собой длину перпендикуляра, который опущен из вершины фигуры на ее основание. Вершиной конуса является точка, ограничивающая коническую поверхность со стороны, противоположной основанию.
Обозначим высоту символом h, а площадь основания символом So, тогда объем конуса через площадь основания запишется так:
V = 1/3*h*So.
Эта формула справедлива для абсолютно любого типа конуса, включая наклонные фигуры.
Объемы кругового и эллиптического конусов
Круговой конус является, пожалуй, самым ярким представителем данного класса фигур. Его можно получить, если вращать треугольник с прямым углом вокруг любого катета. Основание этого конуса является кругом, поэтому его объем можно рассчитать так:
V = 1/3*h*pi*r2.
Где r - радиус круглого основания.
Эллиптический конус также иногда появляется в геометрических задачах, поэтому полезно привести формулу объема для него. Вспоминая, как рассчитывается площадь эллипса, получаем следующее выражение для объема конуса через основания площадь:
V = 1/3*h*pi*a*b.
Здесь a, b - это длины полуосей эллипса.
Отметим, что общая формула объема конуса имеет вид, аналогичный таковому для пирамиды.