Проблема Гольдбаха является одной из старейших и наиболее раскрученных задач в истории всей математики.
Было доказано, что эта гипотеза верна для всех целых чисел, меньших 4 × 1018, но остается недоказанной, несмотря на значительные усилия математиков.
Число
Число Гольдбаха является положительным четным целым числом, являющимся суммой пары нечетных простых чисел. Другой формой утверждения гипотезы Гольдбаха является то, что все четные целые числа большие четырех являются числами Гольдбаха.
 Вам будет интересно:Что это рычаг в физике? Принцип работы рычага. Виды рычагов
Вам будет интересно:Что это рычаг в физике? Принцип работы рычага. Виды рычагов
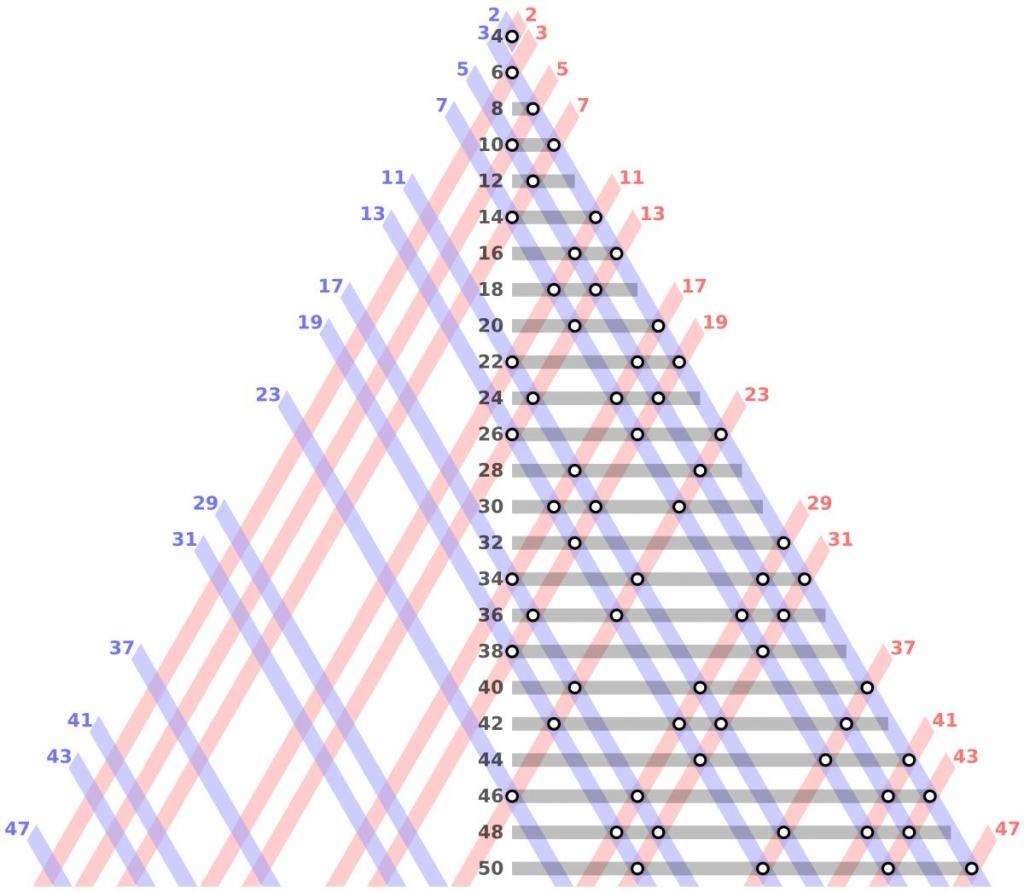
Выделение подобных чисел называется разбиением (или разделом) Гольдбаха. Ниже приведены примеры подобных разделов для некоторых четных чисел:
6 = 3 + 38 = 3 + 510 = 3 + 7 = 5 + 512 = 7 + 5...100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53.
Открытие гипотезы
У Гольдбаха был коллега по фамилии Эйлер, который любил считать, составлять сложные формулы и выдвигать нерешаемые теории. В этом они с Гольдбахом были похожи. Эйлер составил похожую математическую загадку еще до Гольдбаха, с которым вел постоянную переписку. Затем он предложил второе предположение на полях своего манускрипта, согласно которому целое число больше 2 можно записать как сумму трех простых чисел. Он считал 1 простым числом.
Теперь известно, что две гипотезы аналогичны, но в то время это не казалось проблемой. Современная версия проблемы Гольдбаха гласит, что каждое целое число больше 5 можно записать как сумму трех простых чисел. Эйлер ответил в письме от 30 июня 1742 года и напомнил Гольдбаху о более раннем разговоре, который у них был («… итак, мы говорим о первоначальной (а не маргинальной) гипотезе, вытекающей из следующего утверждения»).
Проблема Эйлера-Гольдбаха
2 и четные ему числа могут быть записаны как сумма двух простых чисел, что также является гипотезой Гольдбаха. В письме от 30 июня 1742 года Эйлер заявил, что каждое четное целое число представляет собой результат сложения двух простых, он считает это совершенно определенной теоремой, хотя и не может доказать этого.
Третья версия
Третья версия проблемы Гольдбаха (эквивалентная двум другим версиям) - это форма, в которую гипотеза обычно облекается сегодня. Она также известна как «сильная», «четная» или «бинарная» гипотеза Гольдбаха, чтобы уметь отличать ее от более слабой гипотезы, известной сегодня как «слабая», «нечетная» или «троичная» Гипотеза Гольдбаха. Слабая гипотеза утверждает, что все нечетные числа больше 7 являются суммой трех нечетных простых чисел. Слабая гипотеза была доказана в 2013 году. Слабая гипотеза является следствием сильной гипотезы. Обратное следствие и сильная гипотеза Гольдбаха остаются недоказанными по настоящий день.
Проверка
При малых значениях n проблема Гольдбаха (и, следовательно, гипотеза Гольдбаха) может быть проверена. Например, Нильс Пиппинг в 1938 году тщательно проверил гипотезу до n ≤ 105. С появлением первых компьютеров было просчитано еще множество значений n.
Оливейра Сильва совершил распределенный компьютерный поиск, который подтвердил гипотезу для n ≤ 4 × 1018 (и дважды проверил до 4 × 1017) по состоянию на 2013 год. Одна запись из этого поиска состоит в том, что 3 325 581 707 333 960 528 - это наименьшее число, которое не имеет разбиения Гольдбаха с простым числом ниже 9781.
Эвристика
Версия для сильной формы гипотезы Гольдбаха заключается в следующем: поскольку величина стремится к бесконечности с ростом n, мы ожидаем, что каждое большое четное целое число имеет не только одно представление в виде суммы двух простых чисел. Но самом деле очень много подобных представлений. Кем решена проблема Гольдбаха? Увы, все еще никем.

Этот эвристический аргумент на самом деле несколько неточен, поскольку он предполагает, что m по отношению к n является статистически независимым. Например, если m нечетно, то n - m также нечетно, а если m четно, то n - m четно, и это нетривиальное (сложное) отношение, потому что кроме числа 2 только нечетные числа могут быть простыми. Точно так же, если n делится на 3, а m уже было простым, отличным от 3, то n - m также взаимно простое с 3, поэтому с большей вероятностью будет простым числом в отличие от общего числа. Проводя этот тип анализа более тщательно, Харди и Литтлвуд в 1923 году, в рамках своей знаменитой гипотезы простых кортежей Харди – Литтлвуда, внесли вышеупомянутое уточнение во всю теорию. Но решить проблему это не помогло до сих пор.
Сильная гипотеза
Сильная гипотеза Гольдбаха гораздо сложнее, чем слабая гипотеза Гольдбаха. Позже Шнирельман доказал, что любое натуральное число, большее 1, может быть записано как сумма не более чем простых чисел C, где C - эффективно вычисляемая постоянная. Ее пытались решить многие математики, считая и умножая цифры, предлагая сложные формулы и т.д. Но у них никогда ничего не получалось, ибо гипотеза слишком сложная. Никакие формулы не помогали.
Но стоит слегка отойти от вопроса доказательства проблемы Гольдбаха. Константа Шнирельмана - это наименьшее число C с этим свойством. Сам Шнирельман получил C <800 000. Этот результат впоследствии был дополнен многими авторами, такими как Оливье Рамаре, который в 1995 году показал, что каждое четное число n ≥ 4 на самом деле является суммой не более шести простых чисел. Наиболее известный результат в настоящее время связан с теорией Гольдбаха Харальдом Хельфготтом.
Дальнейшее развитие
В 1924 году Харди и Литтлвуд в предположении Г.Р.Х. показали, что количество четных чисел вплоть до X, нарушающее бинарную проблему Гольдбаха, намного меньше, чем для маленький с.
В 1973 году Чэнь Цзинъюнь попробовал решить эту проблему, но у него не получилось. Он также был математиком, в посему очень любил решать загадки и доказывать теоремы.
В 1975 году двое американских математиков показали, что существуют положительные постоянные c и C - такие, для которых достаточно больших чисел N. В частности, множество четных целых чисел имеет нулевую плотность. Все это пригодилось для работы по решению тернарной проблемы Гольдбаха, которое еще состоится в будущем.
В 1951 году Линник доказал существование такой постоянной K, что каждое достаточно большое четное число является результатом прибавления друг к другу одного простого числа и другого простого числа. Роджер Хит-Браун и Ян-Кристоф Шлаге-Пухта в 2002 году обнаружили, что K = 13 работает. Это очень интересно для всех людей, которые любят прибавлять друг к другу, слагать разные цифры и смотреть, что будет.
Решение проблемы Гольдбаха
Как и во многих известных гипотезах в математике, существует ряд предполагаемых доказательств гипотезы Гольдбаха, ни одно из которых не принято математическим сообществом.
Хотя гипотеза Гольдбаха подразумевает, что каждое положительное целое число больше единицы может быть записано как сумма не более трех простых чисел, не всегда можно найти такую сумму, используя жадный алгоритм, который использует максимально возможное простое число на каждом шаге. Последовательность Пиллаи отслеживает числа, требующие наибольшего числа простых чисел в их жадных представлениях. Поэтому решение проблему Гольдбаха все еще под вопросом. Тем не менее рано или поздно ее, скорее всего, решат.
Существуют теории, аналогичные проблеме Гольдбаха, в которых простые числа заменяются другими конкретными наборами чисел, такими как квадраты.
Кристиан Гольдбах
Кристиан Гольдбах был немецким математиком, который также изучал право. Его помнят сегодня за гипотезу Гольдбаха.
Он всю жизнь работал математиком - очень любил слагать цифры, изобретать новые формулы. Также он знал несколько языков, на каждом из которых вел свой личный дневник. Этими языками были немецкий, французский, итальянский и русский. Также, по некоторым данным, он владел английским и латынью. Он слыл довольно известным математиком еще при жизни. Также Гольдбах был довольно тесно связан с Россией, ведь у него было множество русских коллег и личное расположение царской семьи.

Он продолжал работать во вновь открывшейся Санкт-Петербургской академии наук в 1725 году в качестве профессора математики и историка академии. В 1728 году, когда Петр II стал царем России, Гольдбах стал его наставником. В 1742 году он поступил в МИД России. То есть он, фактически, работал в нашей стране. В то время в Россию приезжали многие ученые, писатели, философы и военные, потому что Россия того времени была страной возможностей вроде Америки. Многие сделали здесь карьеру. И наш герой не исключение.
Кристиан Гольдбах был многоязычен - он писал дневник на немецком и латинском языках, его письма были написаны на немецком, латинском, французском и итальянском языках, а для официальных документов он использовал русский, немецкий и латынь.
Он умер 20 ноября 1764 года в возрасте 74 лет в Москве. День, когда буде решена проблема Гольдбаха, станет достойным чествованием его памяти.
Заключение
Гольдбах был великим математиком, который подарил нам одну из величайших загадок этой науки. Неизвестно, разгадают ли ее когда-нибудь или нет. Известно лишь, что ее предположительное разрешение, как и в случае с теоремой Ферма, откроет новые перспективы для математики. Ее очень любят решать и анализировать математики. Она очень интересная и любопытна и с эвристической точки зрения. Даже студентам-математикам нравится решать задачу-проблему Гольдбаха. А как же иначе? Ведь молодых людей постоянно влечет ко всему яркому, амбициозному и нерешенному, так как за счет преодоления сложностей можно самоутвердиться. Будем надеяться, что в скором времени эта проблема будет решена молодыми, амбициозными, пытливыми умами.