Каждый, кто знаком с техникой и физикой, знает о понятии ускорения. Тем не менее мало кто знает о том, что эта физическая величина имеет две составляющие: ускорение тангенциальное и ускорение нормальное. Рассмотрим подробнее каждое из них в статье.
Что такое ускорение?
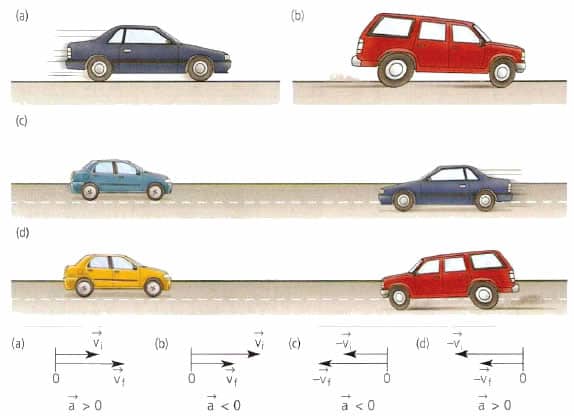
В физике ускорением называют величину, которая описывает быстроту изменения скорости. Причем под этим изменением понимают не только абсолютное значение скорости, но и ее направление. Математически это определение записывают так:
 Вам будет интересно:Бараньи рога: значение и символика
Вам будет интересно:Бараньи рога: значение и символика
a¯ = dv¯/dt.
Заметим, что речь идет о производной изменения вектора скорости, а не только ее модуля.
В отличие от скорости, ускорение может принимать как положительные, так и отрицательные значения. Если скорость направлена всегда вдоль касательной к траектории перемещения тел, то ускорение направлено в сторону действующей на тело силы, что следует из второго закона Ньютона:
F¯ = m*a¯.
Ускорение измеряется в метрах в секунду квадратную. Так, 1 м/с2 означает, что скорость на 1 м/с увеличивается за каждую секунду перемещения.
Прямолинейная и криволинейная траектории движения и ускорение
Окружающие нас объекты могут двигаться либо по прямой линии, либо по кривой траектории, например, по окружности.
В случае движения по прямой скорость тела изменяет только свой модуль, но сохраняет направление. Это означает, что полное ускорение может быть вычислено так:
a = dv/dt.
Отметим, что мы опустили значки вектора над скоростью и ускорением. Поскольку полное ускорение направлено по касательной к прямолинейной траектории, то оно называется тангенциальным или касательным. Эта составляющая ускорения описывает исключительно изменение абсолютной величины скорости.
Теперь предположим, что тело совершает движение по криволинейной траектории. В этом случае его скорость можно представить в виде:
v¯ = v*u¯.
Где u¯ - единичный вектор скорости, направленный вдоль касательной к кривой траектории. Тогда полное ускорение можно записать в такой форме:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Это и есть исходная формула нормального, тангенциального и полного ускорения. Как видно, равенство в правой части состоит из двух слагаемых. Второе из них отлично от нуля только при криволинейном перемещении.
Формулы тангенциального ускорения и нормального ускорения
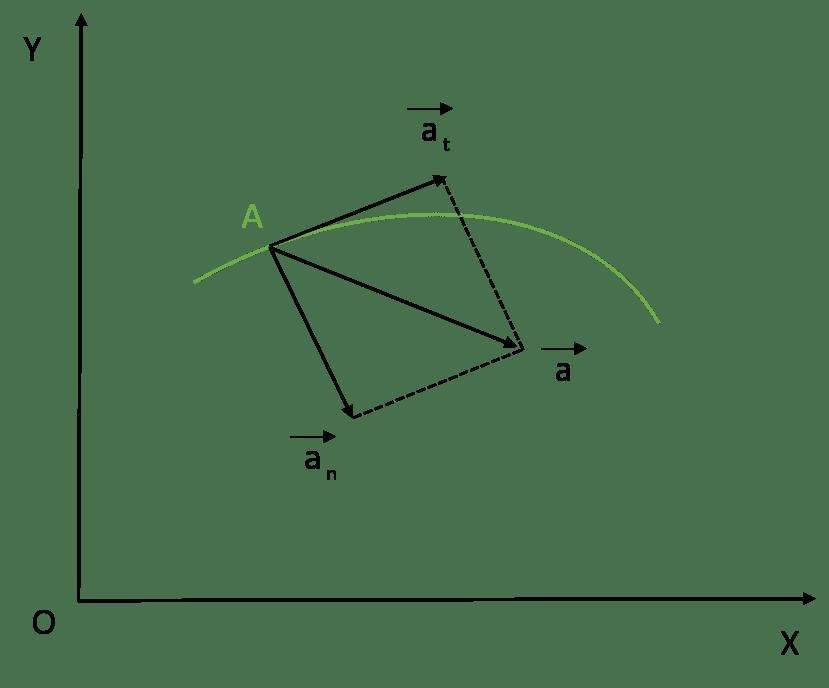
Формула для касательной компоненты полного ускорения уже была приведена выше, запишем ее еще раз:
at¯ = dv/dt*u¯.
Формула показывает, что тангенциальное ускорение не зависит от того, куда направлен вектор скорости, и меняется ли он во времени. Оно определяется исключительно изменением абсолютного значения v.
Теперь запишем вторую компоненту - ускорение нормальное an¯:
an¯ = v*du¯/dt.
Несложно показать геометрически, что эта формула может быть упрощена до такого вида:
an¯ = v2/r*re¯.
Здесь r - кривизна траектории (в случае окружности - это ее радиус), re¯ - элементарный вектор, направленный к центру кривизны. Мы получили интересный результат: от тангенциальной нормальная составляющая ускорения отличается тем, что она совершенно не зависит от изменения модуля скорости. Так, в случае отсутствия этого изменения, касательного ускорения не будет, а нормальное примет некоторое значение.
Нормальное ускорение направлено к центру кривизны траектории, поэтому его называют центростремительным. Причиной его возникновения являются центральные силы в системе, которые изменяют траекторию. Например, это сила гравитации при вращении планет вокруг звезд или сила натяжения веревки при вращении камня, привязанного к ней.
Полное ускорение при вращении по окружности
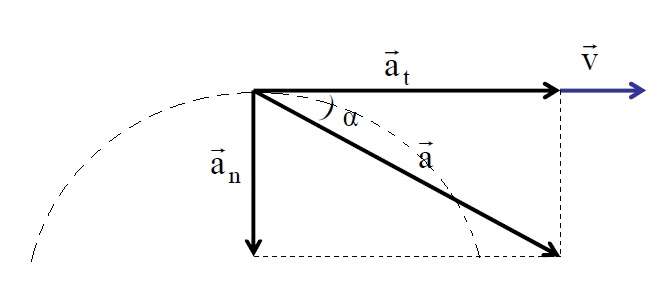
Разобравшись с понятиями и формулами тангенциального ускорения и нормального ускорения, можно теперь переходить к вычислению полного ускорения. Решим эту задачу на примере вращения тела по окружности вокруг некоторой оси.
Рассмотренные две компоненты ускорения направлены под углом 90o друг к другу (по касательной и к центру кривизны). Этот факт, а также свойство суммы векторов можно использовать, чтобы рассчитать ускорение полное. Получаем:
a = √(at2 + an2).
Из формулы полного, нормального и тангенциального ускорений (ускорения an и at) следует два важных вывода:
- В случае прямолинейного перемещения тел полное ускорение совпадает с тангенциальным.
- Для равномерного вращения по окружности полное ускорение имеет только нормальную компоненту.

Во время движения по окружности центростремительная сила, сообщающая телу ускорение an, удерживает его на круговой орбите, препятствуя тем самым фиктивной центробежной силе.
