При изучении абсолютно любой пространственной фигуры важно знать, как рассчитывать ее объем. В данной статье приводится формула объема правильной четырехугольной пирамиды, а также на примере решения задач показано как этой формулой следует пользоваться.
О какой пирамиде пойдет речь?
Каждому школьнику старших классов известно, что пирамида представляет собой многогранник, состоящий из треугольников и многоугольника. Последний является основанием фигуры. Треугольники имеют одну общую сторону с основанием и пересекаются в единственной точке, являющейся вершиной пирамиды.
 Вам будет интересно:Характеристика деятельности: общая, профессиональная, экономическая. Виды деятельности, процесс и общая оценка
Вам будет интересно:Характеристика деятельности: общая, профессиональная, экономическая. Виды деятельности, процесс и общая оценка
Каждая пирамида характеризуется длиной сторон основания, длиной боковых ребер и высотой. Последняя представляет собой перпендикулярный отрезок, опущенный к основанию из вершины фигуры.
Правильная четырехугольная пирамида представляет собой фигуру с квадратным основанием, высота которой пересекает этот квадрат в его центре. Пожалуй, самым известным примером пирамид этого типа являются древние египетские каменные строения. Ниже приведена фотография пирамиды Хеопса.

Изучаемая фигура имеет пять граней, четыре из которых - это одинаковые равнобедренные треугольники. Также она характеризуется пятью вершинами, четыре из которых принадлежат основанию, и восемью ребрами (4 ребра основания и 4 ребра боковых граней).
Формула объема четырехугольной пирамиды правильной
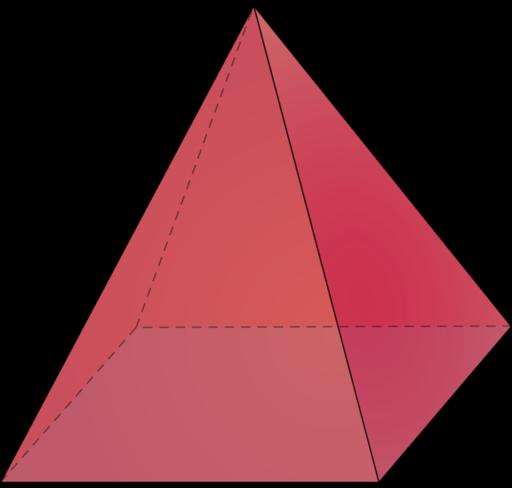
Объем рассматриваемой фигуры представляет собой часть пространства, которое ограничивают пять сторон. Чтобы вычислить этот объем воспользуемся следующей зависимостью площади параллельного основанию пирамиды среза Sz от вертикальной координаты z:
Sz = So * (h - z/h)2
Здесь So - площадь квадратного основания. Если в записанное выражение подставить z = h, то мы получим нулевое значение для Sz. Этой величине z соответствует срез, который будет содержать только вершину пирамиды. Если же z = 0, то мы получаем значение площади основания So.

Объем пирамиды найти несложно, зная функцию Sz(z), для этого достаточно разрезать фигуру на бесконечное число параллельных основанию слоев, а затем провести операцию интегрирования. Следую этой методике, получаем:
V = ∫0h(Sz)*dz = -S0*(h-z)3 / (3*h2)|0h = 1/3*S0*h.
Поскольку S0 - это площадь квадратного основания, то, обозначив сторону квадрата буквой a, получаем формулу объема правильной четырехугольной пирамиды:
V = 1/3*a2*h.
Теперь покажем на примерах решения задач, как следует применять это выражение.
Задача на определение объема пирамиды через ее апофему и боковое ребро
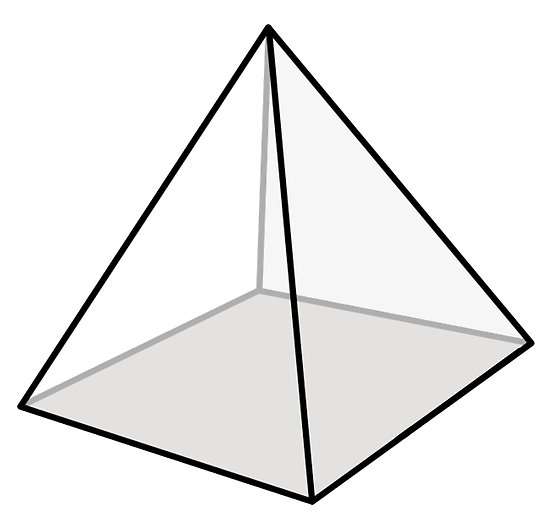
Апофемой пирамиды называют высоту ее бокового треугольника, которая опущена на сторону основания. Поскольку все треугольники равны в правильной пирамиде, то их апофемы также будут одинаковыми. Обозначим ее длину символом hb. Боковое ребро обозначим как b.
Зная, что апофема пирамиды равна 12 см, а ее боковое ребро составляет 15 см, найдите объем правильной пирамиды четырехугольной.
Записанная в предыдущем пункте формула для объема фигуры содержит два параметра: длину стороны a и высоту h. На данный момент нам не известен ни один из них, поэтому займемся их вычислениями.
Длину стороны квадрата a несложно рассчитать, если воспользоваться теоремой Пифагора для треугольника прямоугольного, у которого гипотенузой является ребро b, а катетами будут апофема hb и половина стороны основания a/2. Получаем:
b2 = hb2 + a2/4 =>
a = 2*√(b2 - hb2).
Подставляя известные значения из условия, получим величину a = 18 см.
Чтобы вычислить высоту h пирамиды, можно поступить двумя способами: рассмотреть прямоугольный треугольник с гипотенузой-боковым ребром или с гипотенузой-апофемой. Оба способа равноправны и предполагают выполнение одного и того же количества математических операций. Остановимся на рассмотрении треугольника, где гипотенузой является апофема hb. Катетами в нем будут h и a/2. Тогда получаем:
h = √(hb2-a2/4) = √(122 - 182/4) = 7,937 см.
Теперь можно воспользоваться формулой для объема V:
V = 1/3*a2*h = 1/3*182*7,937 = 857,196 см3.
Таким образом, объем правильной четырехугольной пирамиды равен приблизительно 0,86 литра.
Объем пирамиды Хеопса
Теперь решим интересную и практически важную задачу: найдем, чему равен объем самой большой пирамиды в Гизе. Из литературных данных известно, что исходная высота строения была равна 146,5 метра, а длина его основания составляет 230,363 метра. Эти цифры позволяют применить формулу для вычисления V. Получаем:
V = 1/3*a2*h =1/3*230,3632*146,5 ≈ 2591444 м3.
Полученное значение составляет почти 2,6 млн. м3. Этот объем соответствует объему куба, сторона которого равна 137,4 метра.
