Каждый школьник старших классов знает о таких пространственных фигурах, как шар, цилиндр, конус, пирамида и призма. Из этой статьи вы узнаете о том, что собой представляет треугольная призма, и какими свойствами она характеризуется.
Какую фигуру рассмотрим в статье?
Треугольная призма является самым простым представителем класса призм, который имеет меньшее число сторон, вершин и ребер, чем какая-либо другая подобная пространственная фигура. Эта призма образована двумя треугольниками, которые могут иметь произвольную форму, но которые должны обязательно быть равны друг другу и находиться в параллельных плоскостях в пространстве, и тремя параллелограммами, не равными между собой в общем случае. Для наглядности ниже приведена описанная фигура.
 Вам будет интересно:Скелет крокодила: описание костей, строение и фото
Вам будет интересно:Скелет крокодила: описание костей, строение и фото
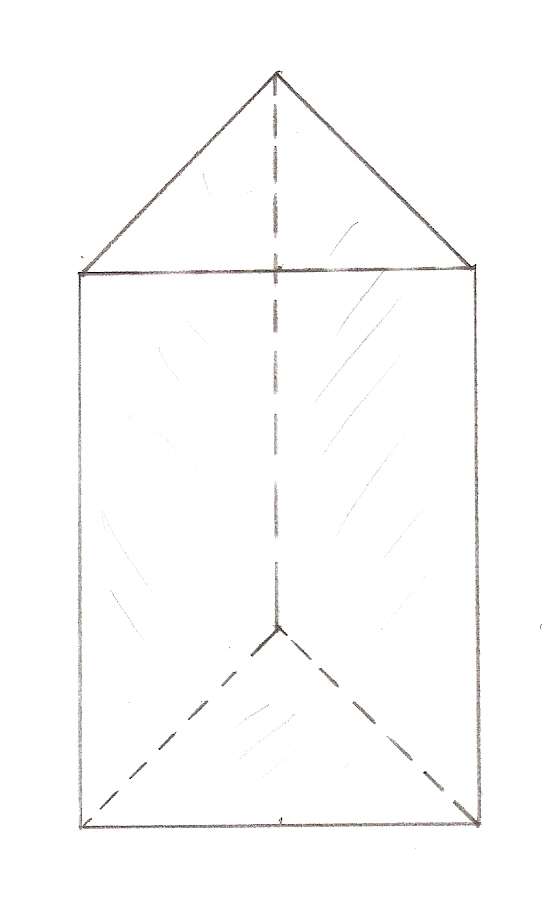
Как можно получить треугольную призму? Очень просто: следует взять треугольник и перенести его на некоторый вектор в пространстве. Затем одинаковые вершины двух треугольников соединить отрезками. Так мы получим каркас фигуры. Если теперь представить, что этот каркас ограничивает сплошные стороны, то мы получим изображенную объемную фигуру.
Из каких элементов состоит изучаемая призма?
Треугольная призма является многогранником, то есть она образована несколькими пересекающимися гранями или сторонами. Выше было указано, что таких сторон у нее пять (две треугольные и три четырехугольные). Треугольные стороны называются основаниями, параллелограммы же являются боковыми гранями.
Как и всякий многогранник, изучаемая призма имеет вершины. В отличие от пирамиды, вершины любой призмы равноправны. У треугольной фигуры их шесть. Все они принадлежат обоим основаниям. В каждой вершине пересекаются два ребра основания и одно боковое ребро.
Если сложить количество вершин с числом сторон фигуры, а затем вычесть из полученного значения число 2, то мы получим ответ на вопрос, сколько ребер имеет рассматриваемая призма. Их девять: шесть ограничивают основания, а оставшиеся три разделяют параллелограммы между собой.
Виды фигуры
Приведенному в предыдущих пунктах достаточно подробному описанию треугольной призмы соответствуют несколько видов фигуры. Рассмотрим их классификацию.
Изучаемая призма может быть наклонной и прямой. Различие между ними заключается в типе боковых граней. В прямой призме они являются прямоугольниками, а в наклонной представляют собой параллелограммы общего вида. Ниже показаны две призмы с треугольными основаниями, одна из которых является прямой, а вторая - наклонной.
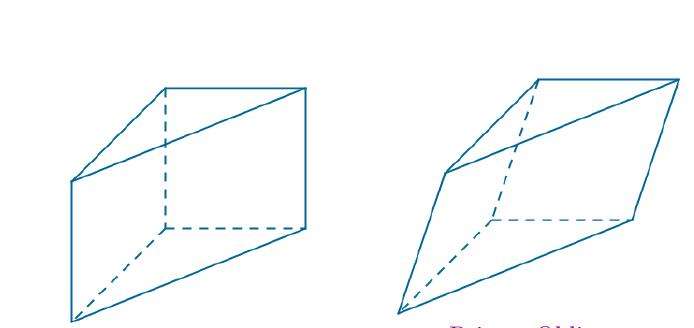
В отличие от наклонной, у прямой призмы все углы двугранные между основаниями и боковыми сторонами равны 90°. Что означает последний факт? Что высота треугольной призмы, то есть расстояние между ее основаниями, у прямой фигуры равна длине любого бокового ребра. У наклонной фигуры высота всегда меньше длины ее любого бокового ребра.
Призма с треугольным основанием может быть неправильной и правильной. Если основания ее являются треугольниками с равными сторонами, и сама фигура является прямой, тогда она называется правильной. Правильная призма обладает достаточно высокой симметрией, включая плоскости отражения и оси поворота. Для правильной призмы ниже будут приведены формулы вычисления ее объема и площади поверхности граней. Итак, по порядку.
Площадь треугольной призмы
Прежде чем переходить к получению соответствующей формулы, приведем развертку правильной призмы.
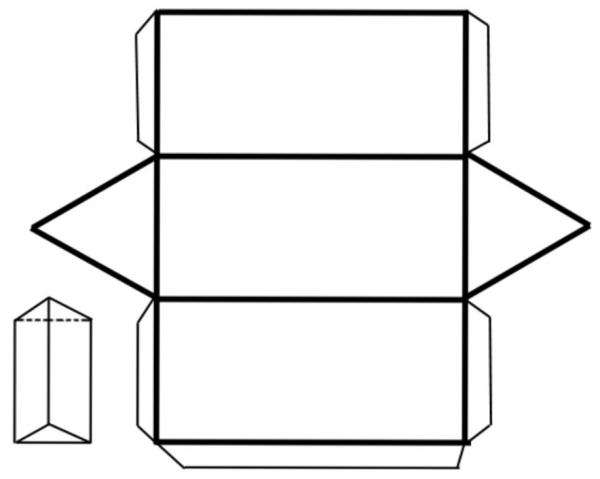
Ясно видно, что площадь фигуры можно вычислить, если сложить три площади одинаковых прямоугольников и две площади равных треугольников с одинаковыми сторонами. Обозначим высоту призмы буквой h, а сторону ее треугольного основания - буквой a. Тогда для площади треугольника S3 имеем:
S3 = √3/4 * a2
Это выражение получается, если умножить высоту треугольника на его основание, а затем результат поделить на 2.
Для площади прямоугольника S4 получаем:
S4 = a * h
Складывая площади всех сторон, получаем полную площадь поверхности фигуры:
S = 2 * S3 + 3 * S4 = √3/2 * a2 + 3 * a * h
Здесь первое слагаемое отражает площадь оснований, а второе - это площадь боковой поверхности треугольной призмы.
Напомним, что эта формула справедлива только для правильной фигуры. В случае неправильной наклонной призмы расчет площади следует производить поэтапно: сначала определить площади оснований, а затем - боковой поверхности. Последняя будет равна произведению бокового ребра на периметр перпендикулярного боковым граням среза.
Объем фигуры

Объем треугольной призмы вычислить можно по общей для всех фигур этого класса формуле. Она имеет вид:
V = So * h
В случае призмы правильной треугольной эта формула примет следующий конкретный вид:
V = √3/4 * a2 * h
Если же призма является неправильной, но прямой, тогда вместо площади основания следует подставить соответствующую площадь для треугольника. Если же призма является наклонной, то, помимо определения площади основания, следует вычислить также ее высоту. Как правило, для этого применяют тригонометрические формулы, если известны двугранные углы между боковыми сторонами и основаниями.
