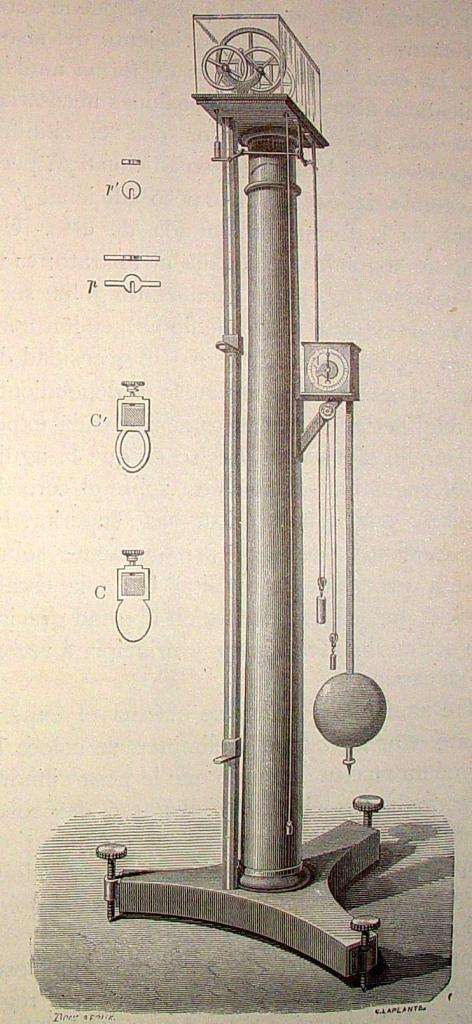
Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
Вам будет интересно:Что такое таксономия? Классификация таксономии
Вам будет интересно:Понятие о полном ускорении. Компоненты ускорения. Ускоренное перемещение по прямой и равномерное движение по окружности
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
F = m*a.
Где m – инерционная масса тела, a – ускорение.
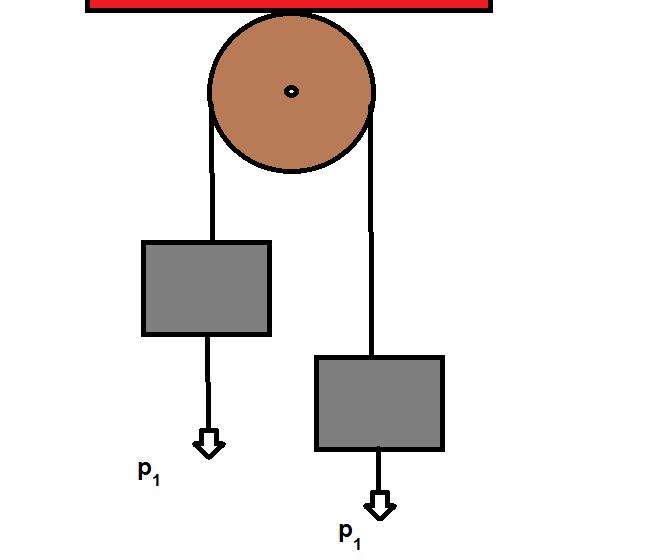
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
F1 – T = m1*a.
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
T – F2 = m2*a.
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
F1 – T = m1*a;
T – F2 = m2*a.
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
F1 – F2 = a*(m1 + m2) =>
a = (F1 – F2)/(m1 + m2).
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
a = g*(m1 – m2)/(m1 + m2).
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
a = na*g.
Проверка решения уравнений динамики
Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
h = a*t2/2.
Откуда ускорение определяется однозначно:
a = 2*h/t2.
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
acp = ∑i=1mai/m.
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
acp = na*g.
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
g = a/na.
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
g = 2*h/(t2*na).
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
F1 = 2*h*m1/(t2*na).
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
F1 – T = m1*a;
T – F2 = m2*a.
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
(F1 – T)/m1 = (T – F2)/m2 =>
T = (m2*F1 + m1*F2)/(m1 + m2).
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
T = 2*m1*m2*g/(m1 + m2).
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
