Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.
Понятие о скорости
Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:
Вам будет интересно:Геометрическая фигура призма. Свойства, виды, формулы объема и площади. Правильная треугольная призма
v¯ = dl¯/dt.
Здесь l¯ - является вектором перемещения. Иными словами, скорость - это производная по времени от пройденного пути.
Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.
Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.
Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.
Понятие об ускорении
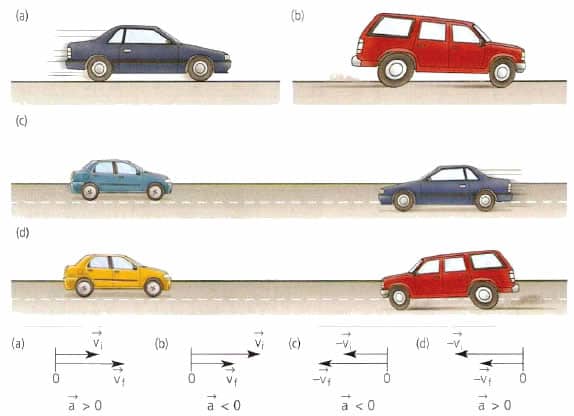
В отличие от скорости, которая характеризует быстроту прохождения телом траектории, ускорение - это величина, описывающая быстроту изменения скорости, что математически записывается так:
a¯ = dv¯/dt.
Как и скорость, ускорение - это векторная характеристика. Однако его направление не связано с вектором скорости. Оно определяется изменением направления v¯. Если в процессе движения скорость не изменяет своего вектора, тогда ускорение a¯ будет направлено вдоль той же линии, что и скорость. Такое ускорение называют тангенциальным. Если же скорость будет менять направление, сохраняя при этом абсолютное значение, то ускорение будет направлено к центру кривизны траектории. Оно называется нормальным.
Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.
Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:
a = F/m.
Эта формула является прямым следствием из второго закона Ньютона.
Полное, нормальное и тангенциальное ускорения
Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:
v¯ = v*u¯.
Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.
Второе слагаемое - это нормальное ускорение. Оно количественно описывает изменение вектора скорости, не принимая во внимание изменение ее модуля.
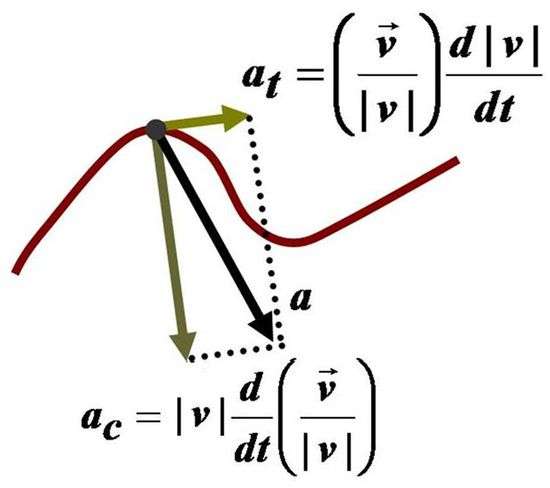
Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:
a = √(at2 + an2).
Связь тангенциального ускорения и скорости
Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:
v = at*t;
v = v0 ± at*t.
В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.
Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:
at = dv/dt.
Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:
at = dv/dt = 9*t2 + 4.
Скорость и нормальное ускорение
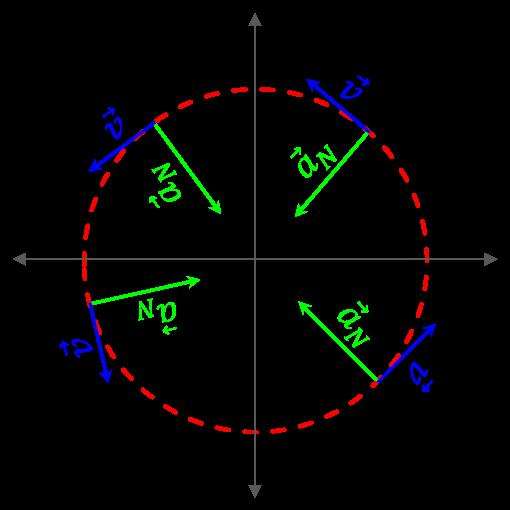
Запишем в явном виде формулу для нормальной компоненты an, имеем:
an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯
Где re¯ - единичной длины вектор, который к центру кривизны траектории направлен. Это выражение устанавливает связь тангенциальной скорости и нормального ускорения. Видим, что последнее зависит от модуля v в данный момент времени и от радиуса кривизны r.
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.