Наука геометрия призвана познакомить школьников со свойствами фигур в двумерном и трехмерном пространстве, а также развить у них абстрактное мышление. Одной из простых фигур, которые помогают справиться с этой задачей, является призма. Что это такое и какими свойствами она обладает, рассматривается в статье.
Призма - совершенный многогранник
Чтобы понять, что это - призма, представим себе многоугольник произвольной формы, расположенный на плоскости. Теперь выполним перенос параллельно самому себе этого многоугольника в новую плоскость и зафиксируем его. Начальный и конечный многоугольники совместно с областью пространства, которую он преодолел в процессе параллельного переноса, образуют фигуру призму. Чтобы нагляднее представить описанную процедуру получения этой фигуры, приведем рисунок.
 Вам будет интересно:Сокрушаться – это проблема или привычка?
Вам будет интересно:Сокрушаться – это проблема или привычка?
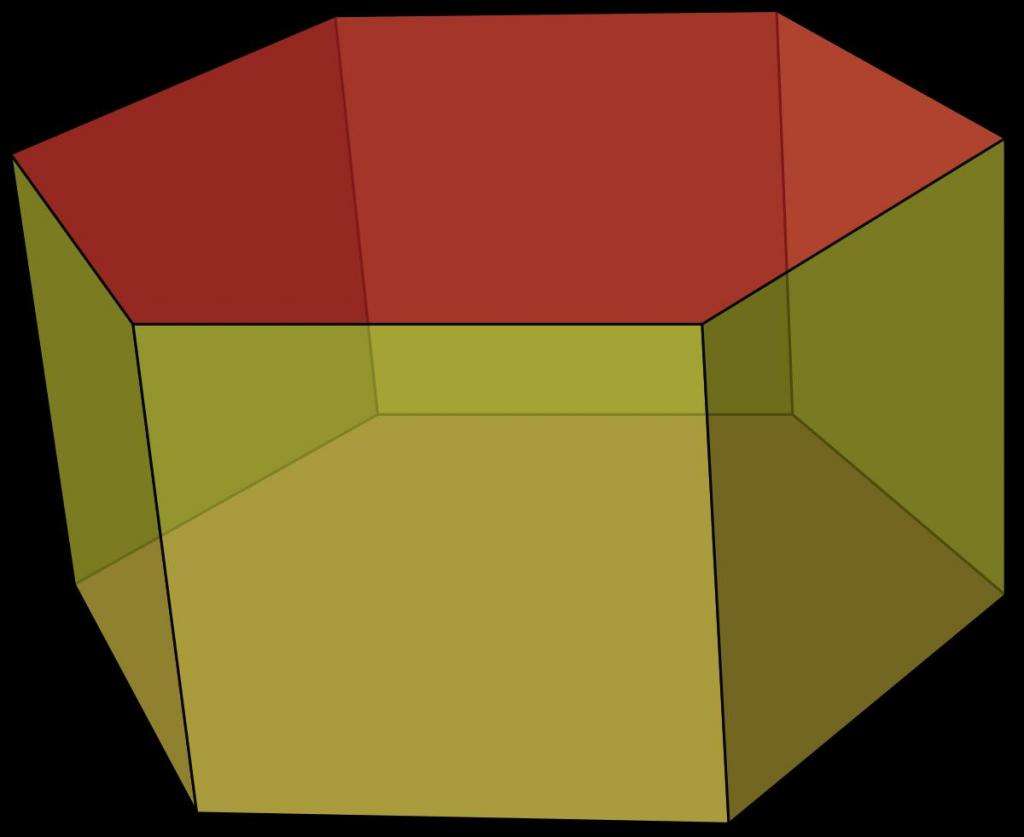
Здесь изображена призма шестиугольная. Красный шестиугольник вверху является исходным, желтый шестиугольник внизу - конечным. Плоские фигуры равны друг другу и лежат в параллельных плоскостях. Они называются основаниями призмы. Шесть боковых граней, которые соединяют одноименные стороны оснований между собой, представляют в общем случае параллелограммы. Однако боковые стороны могут быть также прямоугольниками, квадратами и ромбами.
Элементы призмы
При рассмотрении ответа на вопрос, что это - призма, отмечалось, что изучаемая фигура образована гранями двух типов. Если в основаниях находятся n-угольники, тогда число боковых параллелограммов будет равно n, и общее количество сторон составит n+2.
Стороны - это не единственный элемент изучаемого полиэдра. Призма также имеет несколько вершин и ребер. Вершиной называется точка пересечения двух параллелограммов с основанием. Таких точек у призмы 2*n. Ребром называется отрезок, образованный в результате пересечения двух любых граней фигуры. Призма имеет два типа ребер: относящиеся к основаниям - их 2*n штук, и принадлежащие боковым сторонам - их n штук.
Из названных трех элементов полиэдра, пожалуй, грани являются самыми важными, поскольку их тип определяет конкретный вид призмы.
Каких видов бывают призмы
Как уже отмечалось, вид призмы однозначно определяется формой двух типов граней, образующих фигуру. В геометрии выделяют следующие виды фигур рассматриваемого класса:
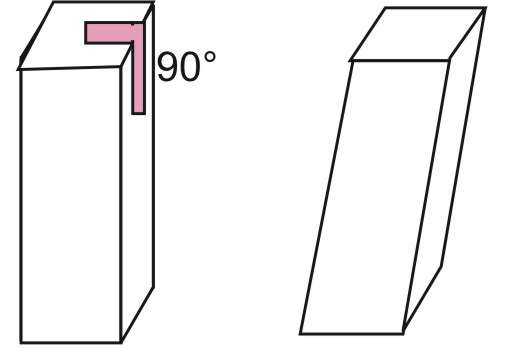
Выше на рисунке показаны две призмы четырехугольные. Левая из них является прямой, а правая - наклонной.
Поверхность призмы
Поверхностью изучаемой фигуры является совокупность точек, которые принадлежат ее граням. Основным свойством поверхности является ее площадь. Эту величину удобно изучать, рассматривая развертку призмы. Развертки двух четырехугольных призм показаны ниже.
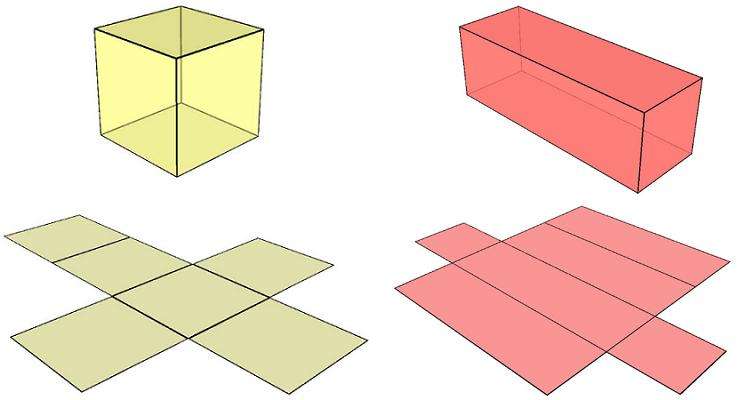
Чтобы найти площадь призмы, необходимо сложить площади двух ее оснований и добавить к ним площадь боковой поверхности. Отмеченные математические операции удобно выполнять для правильных призм, поскольку для них можно записать конкретную формулу для полной площади S.
Площадь правильного n-угольника, имеющего длину стороны a, вычисляется по следующей формуле:
Sn = n/4*ctg(pi/n)*a2
Так как основания призмы равны друг другу, то их суммарная площадь составит:
2*So = n/2*ctg(pi/n)*a2
Боковая поверхность правильной фигуры представлена n одинаковыми прямоугольниками. Обозначив высоту призмы буквой h, запишем формулу для площади Sb боковой поверхности:
Sb = n*a*h
Остается сделать последний шаг - сложить найденные площади оснований и боковой поверхности:
S = 2*So + Sb = n/2*ctg(pi/n)*a2 + n*a*h
Объем фигуры
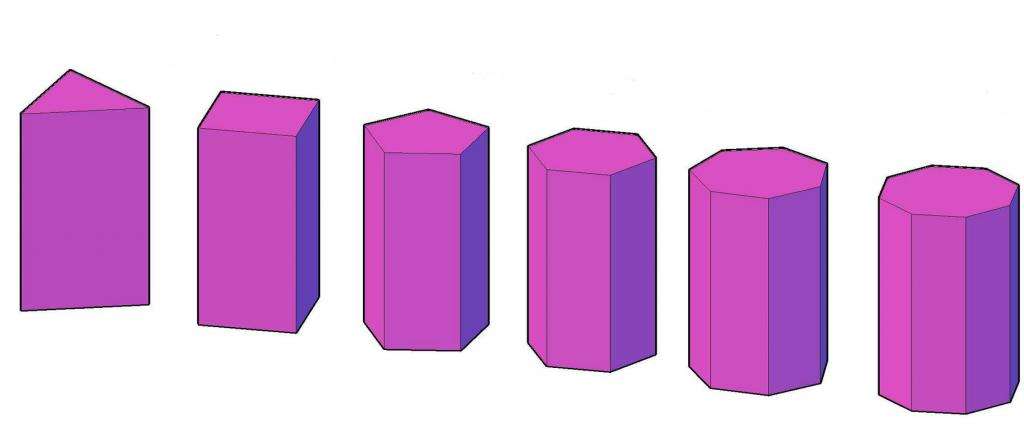
Рассматривая ответ на вопрос, что это - призма, мы выяснили, что речь идет о фигуре, которая обладает некоторым объемом. Объем призмы рассчитать несложно, если известны площадь ее основания и высота. Соответствующая формула выглядит следующим образом:
V = So*h
Если необходимо найти объем наклонной неправильной призмы, тогда следует решать задачу последовательно. Сначала определить площадь основания, применяя известные формулы планиметрии, а затем переходить к вычислению высоты h. В последнем случае следует воспользоваться знанием двугранных углов между параллелограммами и основанием.
В случае правильной фигуры формула для объема приобретает вид:
V = n/4*ctg(pi/n)*a2*h
Где a - сторона основания призмы.
Как видно из записанных выражений для S и V правильной фигуры, для их расчета следует знать два параметра - a и h.
