В геометрии при изучении того или иного класса фигур приводят ряд формул, которые позволяют количественно охарактеризовать рассматриваемый объект с разных сторон. В данной статье будет рассмотрена фигура призма, и формулы площади поверхности и объема для нее будут приведены.
Что понимают под призмой в стереометрии?
Когда говорят о призме, то имеют в виду трехмерный многогранник, который образован двумя одинаковыми плоскими n-угольниками и n параллелограммами. Оба n-угольника должны обязательно находиться в параллельных плоскостях, они называются сторонами оснований фигуры. Что касается параллелограммов, то они образуют боковую поверхность и могут представлять собой ромбы, прямоугольники и квадраты.
 Вам будет интересно:Чистоплотность — это что такое: толкование
Вам будет интересно:Чистоплотность — это что такое: толкование
Как всякий многогранник, призма состоит из вершин, ребер и граней. Про грани мы уже упомянули. Вершины призмы, в отличие от вершин пирамиды, являются равноправными и принадлежат основаниям. Ребра призмы бывают двух видов: принадлежащие основаниям и относящиеся к боковым граням.
При формировании названия конкретной призмы в него включают четыре типа классификации. Эти типы проще понять, если привести пару примеров.
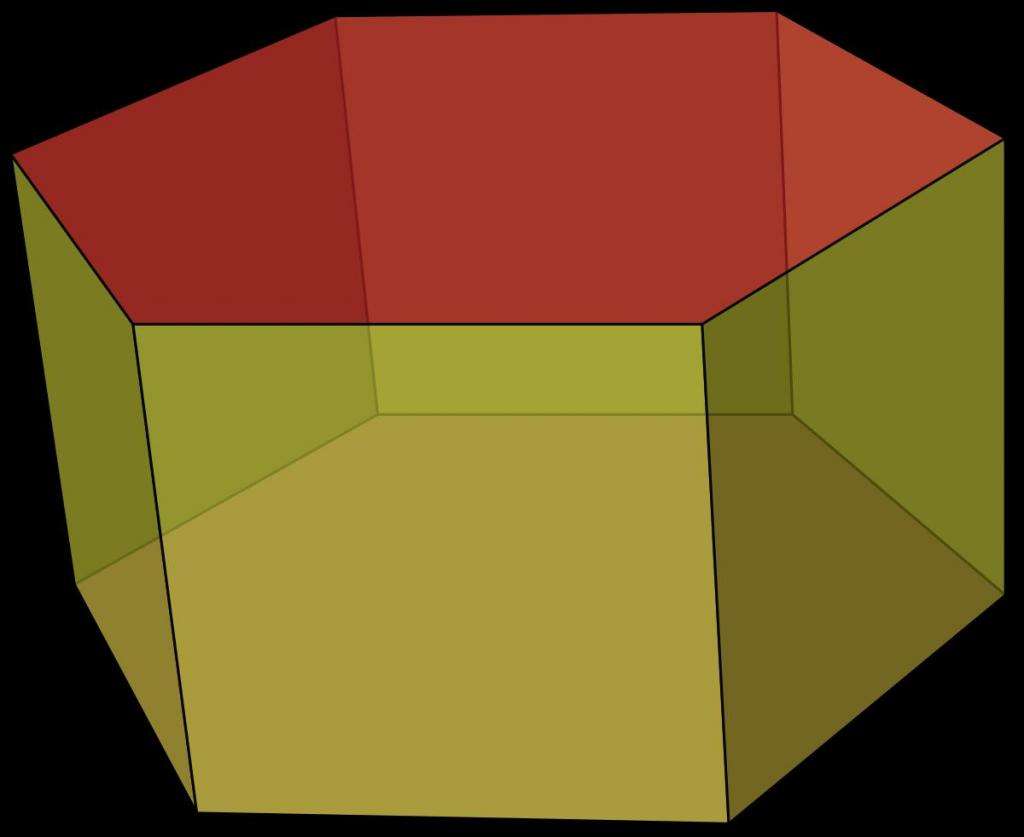
На рисунке выше показана шестиугольная выпуклая правильная прямая фигура. Шестиугольной и выпуклой она называется потому, что основанием ее является выпуклый шестиугольник. Правильной и прямой фигура является потому, что сам шестиугольник имеет равные стороны и углы, а боковая поверхность представлена одинаковыми прямоугольниками.
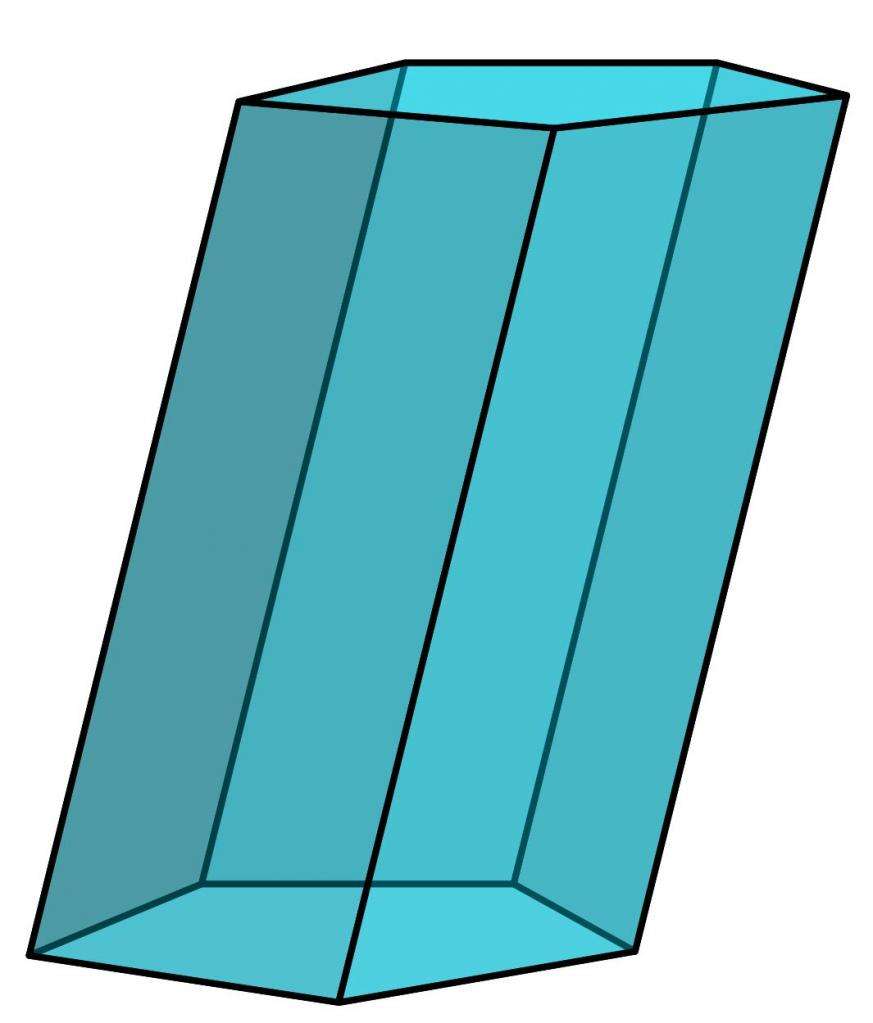
На этом рисунке изображена пятиугольная выпуклая неправильная наклонная призма. Предлагаем читателю самостоятельно разобраться, почему ей дано такое название.
Линейные и угловые параметры призм
Для произвольной призмы однозначное описание ее характеристик требует знания линейных параметров и двугранных углов между ее гранями. Главными линейными параметрами являются длины сторон ai основания, длина ребра бокового b и высота h. Заметим, что стороны основания могут иметь различные длины, боковые же ребра даже в наклонной фигуре равны друг другу. Для прямой и правильной призм длина ребра бокового b совпадает с высотой h (b=h). Для вычисления высоты призмы наклонной необходимо знать значения углов двугранных между плоскостями основания и боковыми параллелограммами.
Знание перечисленных линейных параметров позволяет вычислить площадь поверхности фигуры и ее объем.
Поверхность фигуры
Одними из важных формул призмы являются выражения, позволяющие вычислить ее площадь. Для определения площади всех граней фигуры удобно развернуть ее на плоскости. Пример одной из разверток приведен ниже.
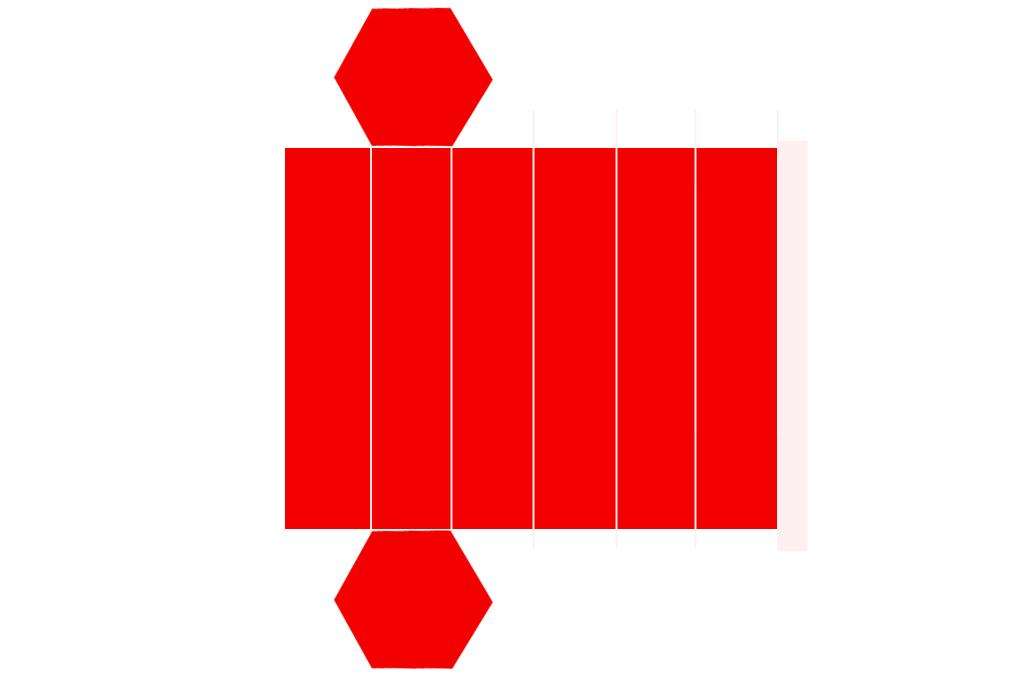
Для произвольной призмы формула площади всей поверхности определяется так:
S = 2*So + Sb = 2*So + b*Psr
Где So - площадь одного основания, Psr - периметр перпендикулярного всем боковым граням среза.
В случае правильной призмы формула для S принимает вид:
S = n/2*ctg(pi/n)*a2 + n*a*h
Здесь n - число вершин (сторон) многоугольника в основании. Первое слагаемое здесь отражает две площади оснований, второе слагаемое - это сумма площадей всех боковых прямоугольников призмы.
Например, формула призмы треугольной правильной примет вид:
S3 = √3/2*a2 + 3*a*h
Отметим, что для определения площади любой правильной фигуры достаточно знать два ее любых параметра. В данном случае этими параметрами являются сторона основания a и высота h.
Формулы для расчета объема
Под объемом многогранника понимают часть пространства, которая заключена между его гранями. Для вычисления объема произвольного вида призмы необходимо воспользоваться той же самой формулой, что и для объема цилиндра. Она имеет следующий вид:
V = So*h
Несмотря на простоту этого выражения, расчет может осложняться тем, что сначала нужно вычислить высоту и площадь основания. Для наклонной призмы с неправильным выпуклым или вогнутым основанием эта задача не является тривиальной и не имеет общего решения. В таком случае следует воспользоваться общим подходом: зная двугранный угол при основании и одну из диагоналей основания или боковое ребро, можно вычислить высоту фигуры; площадь многоугольного основания складывается из площадей элементарных фигур, формулы для которых известны.
Если изучаемая призма является правильной, тогда для нее можно записать конкретное выражение. Формула объема призмы правильной принимает вид:
V = n/4*ctg(pi/n)*a2*h

Например, для треугольной фигуры получаем:
V3 = √3/4*a2*h
Как и для площади S, для определения объема V правильной фигуры необходимо знать высоту и сторону основания.
