Псевдослучайное число — это особая цифра, создаваемая специальным генератором. Генератор таких чисел (PRNG), также известный как генератор детерминированных случайных битов (DRBG), представляет собой алгоритм для создания последовательности чисел, свойства которой аппроксимируют характеристики последовательностей случайных чисел. Генерируемая PRNG последовательность не является действительно случайной, поскольку она полностью определяется начальным значением, называемым начальным числом PRNG, которое может включать в себя действительно случайные значения. Хотя последовательности, которые ближе к случайным, могут создаваться с использованием аппаратных генераторов случайных чисел, генераторы псевдослучайных чисел на практике важны для скорости генерации чисел и их воспроизводимости.
Вам будет интересно:Понятие ориентировки в пространстве и ее развитие
Применение
PRNG являются центральными в таких приложениях, как моделирование (например, для метода Монте-Карло), электронные игры (например, для процедурной генерации) и криптография. Криптографические приложения требуют, чтобы выходные данные не были предсказуемыми из более ранней информации. Требуются более сложные алгоритмы, которые не наследуют линейность простых PRNG.
Требования и условия
Вам будет интересно:Артур, повесь абажур. Рифма к имени Артур
Хорошие статистические свойства являются центральным требованием для получения PRNG. В общем, необходим тщательный математический анализ, чтобы иметь уверенность в том, что ГСЧ генерирует числа, которые достаточно близки к случайным, чтобы соответствовать предполагаемому использованию.
Джон фон Нейман предупредил о неправильной интерпретации PRNG как действительно случайного генератора и пошутил, что «любой, кто рассматривает арифметические методы получения случайных цифр, конечно, находится в состоянии греха».
Использование
PRNG может быть запущен из произвольного начального состояния. Он всегда будет генерировать одну и ту же последовательность при инициализации с этим состоянием. Период PRNG определяется следующим образом: максимум по всем начальным состояниям длины бесповторного префикса последовательности. Период ограничен числом состояний, обычно измеряемых в битах. Поскольку длина периода потенциально удваивается с каждым добавленным битом «состояния», легко создавать PRNG с периодами, достаточно большими для многих практических применений.
Вам будет интересно:Землеустройство и кадастры - специальность: что это такое? Государственный университет по землеустройству
Если внутреннее состояние PRNG содержит n битов, его период может быть не более 2n результатов, он намного короче. Для некоторых PRNG продолжительность может быть рассчитана без обхода всего периода. Регистры сдвига с линейной обратной связью (LFSR) обычно выбираются так, чтобы иметь периоды, ровные 2n − 1.
Линейные конгруэнтные генераторы имеют периоды, которые можно рассчитать с помощью факторинга. Хотя ГСЧП будут повторять свои результаты после того, как они достигнут конца периода, повторный результат не означает, что конец периода был достигнут, так как его внутренние состояние может быть больше, чем выход; это особенно очевидно для PRNG с однобитовым выводом.
Возможные ошибки
Ошибки, обнаруживаемые дефектными PRNG, варьируются от незаметных (и неизвестных) до очевидных. Примером может служить алгоритм случайных чисел RANDU, который десятилетиями использовался на мэйнфреймах. Это был серьезный недостаток, но его неадекватность оставалась незамеченной в течение долгого периода времени.
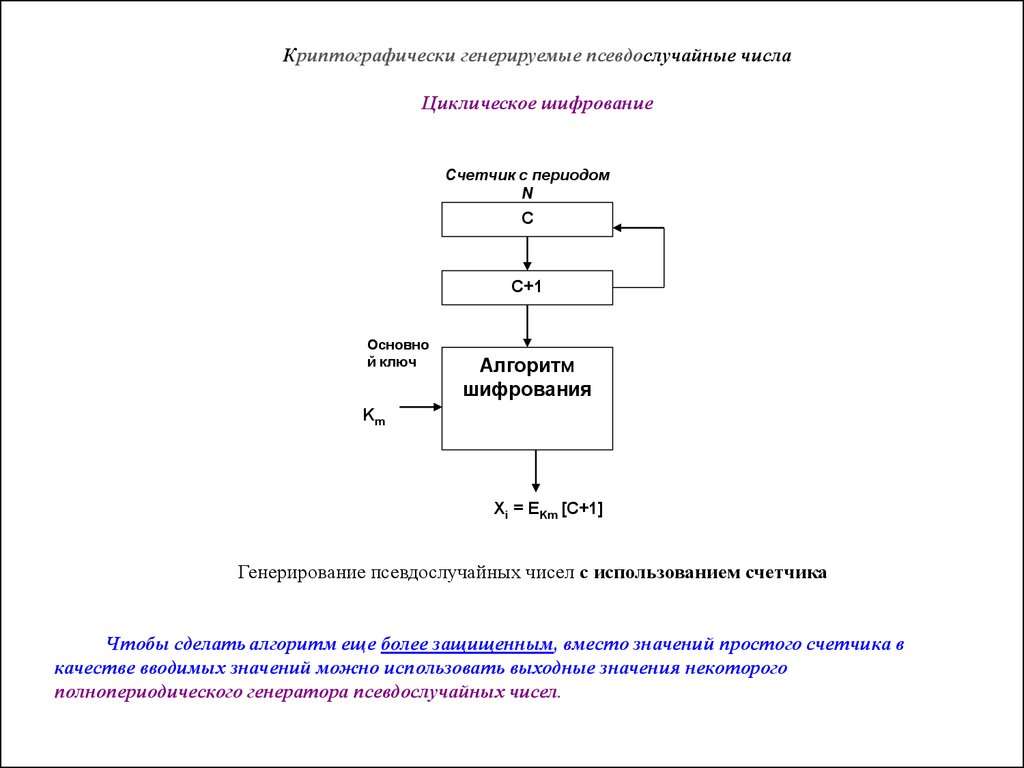
Во многих областях исследовательские работы, в которых использовался случайный отбор, моделирование по методу Монте-Карло или другие способы, основанные на ГСЧП, гораздо менее надежны, чем это могло быть в результате использования ГНПГ низкого качества. Даже сегодня иногда требуется осторожность, о чем свидетельствует предупреждение, приведенное в Международной энциклопедии статистической науки (2010).
Пример успешного применения
В качестве иллюстрации рассмотрим широко используемый язык программирования Java. По состоянию на 2017 год, Java все еще полагается на линейный конгруэнтный генератор (LCG) для своего PRNG.
История
Вам будет интересно:Супружество - это что такое? Значение, происхождение, синонимы
Первым PRNG, который избежал серьезных проблем и все еще работал довольно быстро, был Mersenne Twister (обсуждаемый ниже), информацию о котором опубликовали в 1998 году. С тех пор были разработаны другие высококачественные PRNG.
Но история псевдослучайных чисел этим не исчерпывается. Во второй половине 20-го века стандартный класс алгоритмов, используемых для PRNG, включал линейные конгруэнтные генераторы. Было известно, что качество LCG неадекватно, но лучшие методы были недоступны. Press et al (2007) описал результат следующим образом: «Если бы все научные статьи, результаты которых вызывают сомнения из-за [LCG и связанных с ними] исчезли с библиотечных полок, на каждой полке был бы промежуток размером с ваш кулак».
Основным достижением в создании псевдослучайных генераторов стало внедрение методов, основанных на линейных рекуррентных в двухэлементном поле; такие генераторы связаны с линейными регистрами сдвига с обратной связью. Они послужили основой для изобретения датчиков псевдослучайных чисел.
В частности, изобретение 1997 года Мерсена Твистера позволило избежать многих проблем с более ранними генераторами. Mersenne Twister имеет период 219937−1 итераций (≈4,3 × 106001). Доказано, что он равномерно распределен в (до) 623 измерениях (для 32-битных значений), и на момент его внедрения работал быстрее, чем другие статистически обоснованные генераторы, создающие псевдослучайные последовательности чисел.
В 2003 году Джордж Марсаглия представил семейство генераторов ксоршифтов, основанных также на линейном повторении. Такие генераторы чрезвычайно быстры и — в сочетании с нелинейной операцией — они проходят строгие статистические тесты.
В 2006 году было разработано семейство генераторов WELL. Генераторы WELL в некотором смысле улучшают качество Twister Mersenne, который имеет слишком большое пространство состояний и очень медленное восстановление из них, генерируя псевдослучайные числа c большим количеством нулей.
Криптография
PRNG, подходящий для криптографических приложений, называется криптографически защищенным PRNG (CSPRNG). Требование к CSPRNG состоит в том, что злоумышленник, не знающий начального числа, имеет лишь незначительное преимущество в различении выходной последовательности генератора от случайной последовательности. Другими словами, в то время как PRNG требуется только для прохождения определенных статистических тестов, CSPRNG должен пройти все статистические тесты, которые ограничены полиномиальным временем в размере семени.
Хотя доказательство этого свойства выходит за рамки современного уровня теории вычислительной сложности, убедительные доказательства могут быть предоставлены путем сведения CSPRNG к проблеме, которая считается сложной, подобно целочисленной факторизации. В общем, могут потребоваться годы обзора, прежде чем алгоритм может быть сертифицирован как CSPRNG.
Было показано, что вполне вероятно АНБ вставило асимметричный черный ход в сертифицированный NIST генератор псевдослучайных чисел Dual_EC_DRBG.
Алгоритмы псевдослучайных чисел
Большинство алгоритмов PRNG производят последовательности, которые равномерно распределены любым из нескольких тестов. Это открытый вопрос. Он один из центральных в теории и практике криптографии: есть ли способ отличить выход высококачественного PRNG от действительно случайной последовательности? В этой настройке распознаватель знает, что либо использовался известный алгоритм PRNG (но не состояние, с которым он был инициализирован), либо применялся действительно случайный алгоритм. Он должен различать их.
Безопасность большинства криптографических алгоритмов и протоколов, использующих PRNG, основана на предположении, что невозможно отличить применение подходящего PRNG от использования действительно случайной последовательности. Простейшими примерами этой зависимости являются потоковые шифры, которые чаще всего работают, исключая или отправляя открытый текст сообщения с выходом PRNG, создавая зашифрованный текст. Разработка криптографически адекватных PRNG чрезвычайно сложна, поскольку они должны соответствовать дополнительным критериям. Размер его периода является важным фактором криптографической пригодности PRNG, но не единственным.
Ранний компьютерный PRNG, предложенный Джоном фон Нейманом в 1946 году, известен как метод средних квадратов. Алгоритм следующий: возьмите любое число, возведите его в квадрат, удалите средние цифры полученного числа как «случайное число», затем используйте это число в качестве начального для следующей итерации. Например, возведение в квадрат числа 1111 дает 1234321, которое можно записать как 01234321, 8-значное число является квадратом 4-значного. Это дает 2343 как «случайное» число. Результат повторения этой процедуры — 4896 и так далее. Фон Нейман использовал 10-значные числа, но процесс был таким же.
Недостатки «среднего квадрата»
Проблема с методом «среднего квадрата» заключается в том, что все последовательности в конечном итоге повторяются, некоторые — очень быстро, например: 0000. Фон Нейман знал об этом, но он нашел подход, достаточный для своих целей, и беспокоился, что математические «исправления» будут просто скрывать ошибки, а не удалять их.
Фон Нейманн счел аппаратные генераторы случайных и псевдослучайных чисел неподходящими: если они не записывают сгенерированный вывод, то не могут быть позже проверены на ошибки. Если бы они записывали свои результаты, то исчерпали бы ограниченную доступную память компьютера и, соответственно, способность компьютера читать и записывать числа. Если бы числа были записаны на карточках, им понадобилось бы гораздо больше времени, чтобы писать и читать. На компьютере ENIAC, который он использовал, метод «среднего квадрата» и осуществил процесс получения псевдослучайных чисел в несколько сотен раз быстрее, чем происходит считывание чисел с перфокарт.
Метод среднего квадрата с тех пор был вытеснен более сложными генераторами.
Новаторский метод
Недавнее новшество — объединить средний квадрат с последовательностью Вейля. Этот метод обеспечивает высокое качество продукции в течение длительного периода. Он помогает получать лучшие формулы псевдослучайных чисел.