Пространственная геометрическая фигура призма является объектом изучения стереометрии. Ее характеристики рассматривают в 10-11 классах школ. Данная статья посвящена изучению свойств правильной призмы на примере треугольной, четырехугольной и шестиугольной фигур.
Призма в стереометрии
Данная фигура представляет собой многогранник или полиэдр, состоящий из нескольких параллелограммов и двух одинаковых многоугольников произвольного типа. Оба многоугольника находятся в параллельных плоскостях. Они называются основаниями фигуры. Пример пятиугольной призмы, сделанной из бумаги, показан ниже.
 Вам будет интересно:Псевдослучайное число: методы получения, достоинства и недостатки
Вам будет интересно:Псевдослучайное число: методы получения, достоинства и недостатки

Эту фигуру можно получить в пространстве, если взять пятиугольник и переместить его без вращения в новую плоскость, параллельную исходной.
Призма состоит из граней (n+2), вершин (2*n) и ребер (3*n). В зависимости от типа граней говорят о прямых, наклонных, вогнутых, правильных, четырехугольных и других видах призм.
При изучении этого класса фигур в стереометрии большое внимание уделяется рассмотрению свойств правильных призм.
Что собой представляет правильная фигура?
Правильной называется любая призма, которая является прямой и имеет равносторонние и равноугольные основания. Прямая призма - это пространственная фигура, у которой боковая поверхность вместо параллелограммов общего типа образована прямоугольниками или квадратами. У правильной призмы геометрические центры обоих оснований лежат на одной вертикальной прямой. Важным свойством рассматриваемого вида фигур является то, что длины боковых ребер соответствуют высоте.
Если призма является прямой, но ее основание представляет собой произвольный многоугольник, например, ромб, то такая фигура правильной не будет. Правильное основание предполагает равенство у него всех углов и сторон. Например, равносторонний треугольник имеет три угла по 60o, а у правильного шестиугольника эти углы равны 120o.
Далее в статье приведем такие свойства правильной призмы, как площадь поверхности, объем и длина диагоналей на примере треугольной, четырехугольной и шестиугольной фигур.
Призма с треугольным основанием

Эта призма показана выше на рисунке. Она образована двумя треугольниками равносторонними и тремя прямоугольниками. Приведем свойства и формулы призмы правильной треугольной.
Пусть сторона основания равна a, а высота (длина бокового ребра) составляет h. Тогда площадь поверхности фигуры рассчитывается так:
S = √3/2*a2 + 3*a*h.
Первое слагаемое в правой части равенства соответствует двум площадям оснований, второе слагаемое - это площадь трех прямоугольников, составляющих боковые поверхности.
Для определения объема фигуры следует воспользоваться такой формулой:
V = √3/4*a2*h.
Это выражение получается из общей формулы для объема призмы (произведение высоты на площадь основания).
Треугольная призма обладает одним единственным типом диагоналей - это диагонали прямоугольников. Значение их длины вычисляется так:
d = √(a2 + h2).
Четырехугольная призма
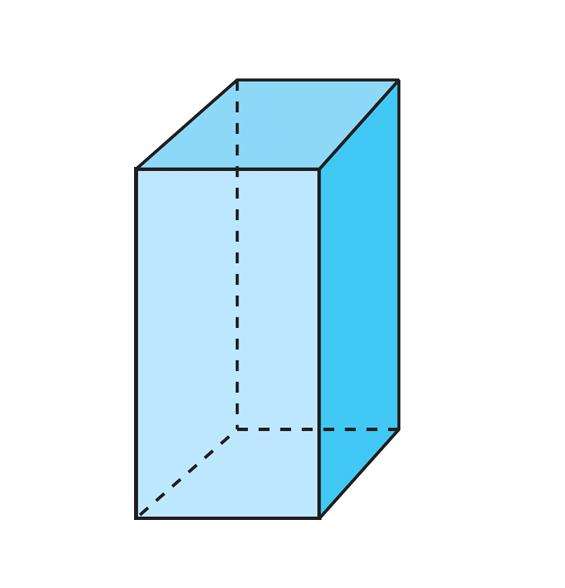
Прежде чем рассматривать свойства правильной призмы четырехугольной, скажем, что она состоит из двух одинаковых квадратов, которые соединены четырьмя прямоугольниками. Многим школьникам эта фигура известна под названием прямоугольного параллелепипеда. Если его высота совпадает со стороной основания, то параллелепипед вырождается в куб.
Площадь поверхности изучаемой симметричной фигуры можно рассчитать по следующей простой формуле:
S = 2*a2 + 4*a*h = 2*a*(a + 2*h).
Чтобы вычислить объем, следует применить такое выражение:
V = a2*h.
При решении задач по геометрии часто возникает проблема определения длины объемных диагоналей прямоугольного параллелепипеда с квадратным основанием. Фигура обладает четырьмя объемными диагоналями. Их длины являются одинаковыми. Для определения этих длин следует применить формулу:
d = √(2*a2 + h2).
Если в формулах для S, V и d заменить параметр h на величину a, то мы получим соответствующие выражения для куба.
Призма шестиугольная

В отличие от предыдущих призм, правильная шестиугольная фигура является более сложной. Эта сложность проявляется в вычислении площади основания, а также в определении длин объемных диагоналей (у фигуры имеется два типа диагоналей).
Свойства призмы правильной шестиугольной начнем рассматривать с определения площади ее поверхности. Состоит она из двух правильных шестиугольников и шести прямоугольников. Соответствующая формула имеет вид:
S = 3*√3*a2 + 6*a*h.
Площадь одного шестиугольника со стороной a равна площади шести равносторонних треугольников с той же длиной стороны.
Для определения объема фигуры следует подставить значения стороны a и высоты h в следующее равенство:
V = 3*√3/2*a2*h.
Как было отмечено выше, существуют два типа объемных диагоналей у шестиугольной призмы. Один тип диагоналей образован в результате соединения противоположных вершин оснований, другой тип - в результате соединения вершин оснований через одну. Рассчитываются длины этих диагоналей так:
d1 = √(4*a2 + h2);
d2 = √(3*a2 + h2).
Формулы показывают, что диагональ первого типа всегда длиннее диагонали второго типа (d1>d2).
