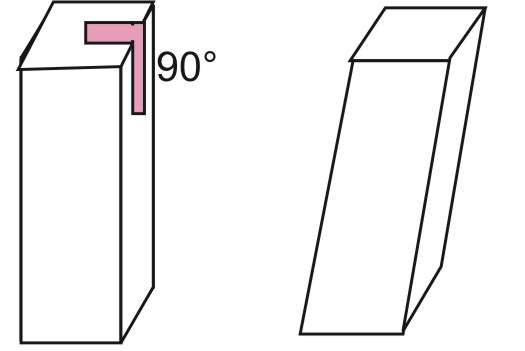
Стереометрия является важной частью общего курса геометрии, которая рассматривает характеристики пространственных фигур. Одной из таких фигур является четырехугольная призма. В данной статье подробнее раскроем вопрос, как рассчитывать объем призмы четырехугольной.
Что собой представляет призма четырехугольная?
Очевидно, что прежде чем приводить формулу объема призмы четырехугольной, необходимо дать ясное определение этой геометрической фигуры. Под такой призмой понимают трехмерный многогранник, который ограничен двумя произвольными одинаковыми четырехугольниками, лежащими в параллельных плоскостях, и четырьмя параллелограммами.
 Вам будет интересно:"Неволить": значение слова, примеры употребления
Вам будет интересно:"Неволить": значение слова, примеры употребления
Отмеченные параллельные друг другу четырехугольники называются основаниями фигуры, а четыре параллелограмма - это боковые стороны. Здесь следует пояснить, что параллелограммы также являются четырехугольниками, однако основания не всегда являются параллелограммами. Пример неправильного четырехугольника, который вполне может быть основанием призмы, показан ниже на рисунке.
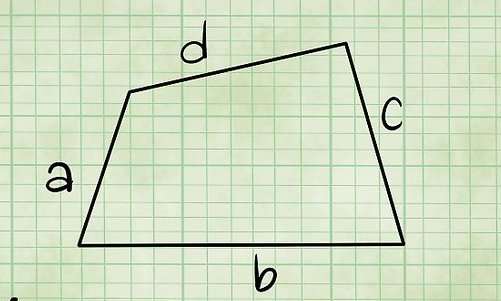
Любая четырехугольная призма состоит из 6 сторон, 8 вершин и 12 ребер. Существуют четырехугольные призмы разных видов. Например, фигура может быть наклонной или прямой, неправильной и правильной. Далее в статье покажем, как можно рассчитывать объем призмы четырехугольной с учетом ее вида.
Наклонная призма с неправильным основанием
Это самый несимметричный вид четырехугольной призмы, поэтому расчет ее объема будет относительно сложным. Определить объем фигуры позволяет следующее выражение:
V = So*h
Символом So здесь обозначена площадь основания. Если это основание представляет собой ромб, параллелограмм или прямоугольник, то рассчитать величину So несложно. Так, для ромба и параллелограмма справедлива формула:
So = a*ha
где a - сторона основания, ha - длина опущенной на эту сторону из вершины основания высоты.
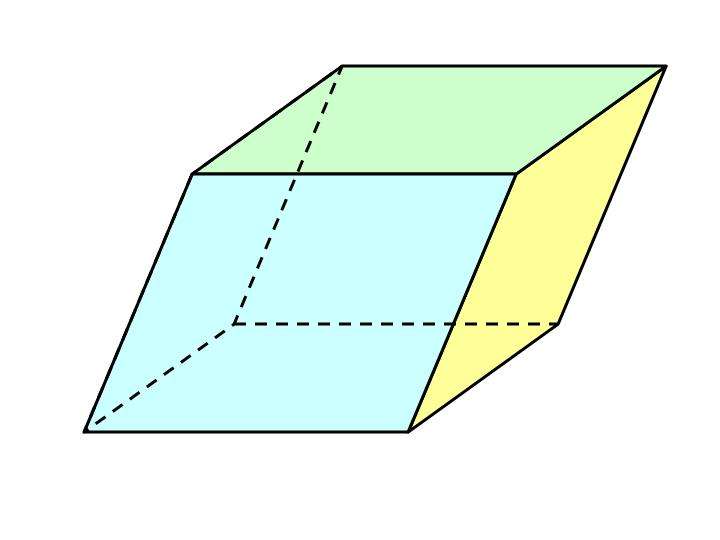
Если основание представляет собой неправильный многоугольник (см. выше), то его площадь следует разбить на более простые фигуры (например, треугольники), вычислить их площади и найти их сумму.
В формуле для объема символом h обозначена высота призмы. Она представляет собой длину перпендикулярного отрезка между двумя основаниями. Поскольку призма является наклонной, то расчет высоты h следует проводить с использованием длины бокового ребра b и двугранных углов между боковыми гранями и основанием.
Правильная фигура и ее объем
Если основанием четырехугольной призмы является квадрат, а сама фигура будет прямой, то она называется правильной. Следует пояснить, что прямой призма называется тогда, когда все ее боковые стороны являются прямоугольниками и каждый из них перпендикулярен основаниям. Правильная фигура показана ниже.
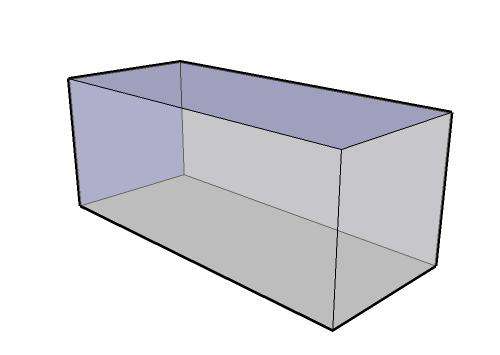
Объем правильной четырехугольной призмы может быть вычислен по той же формуле, что и объем неправильной фигуры. Поскольку основанием является квадрат, то его площадь вычисляется просто:
So = a2
Высота призмы h равна длине бокового ребра b (сторона прямоугольника). Тогда объем правильной призмы четырехугольной может быть рассчитан по следующей формуле:
V = a2*h = a2*b
Правильная призма с квадратным основанием называется прямоугольным параллелепипедом. Этот параллелепипед в случае равенства сторон a и b становится кубом. Объем последнего рассчитывается так:
V = a3
Записанные формулы для объема V свидетельствуют о том, что чем выше симметрия фигуры, тем меньше линейных параметров требуется для вычисления этой величины. Так, в случае правильной призмы необходимое число параметров равно двум, а в случае куба - одному.
Задача с правильной фигурой
Рассмотрев вопрос нахождения объема призмы четырехугольной с точки зрения теории, применим полученные знания на практике.
Известно, что правильный параллелепипед имеет длину диагонали основания, равную 12 см. Длина диагонали его боковой стороны составляет 20 см. Необходимо рассчитать объем параллелепипеда.
Обозначим диагональ основания символом da, а диагональ боковой грани - символом db. Для диагонали da справедливы выражения:
da = a*√2 =>
a = da/√2
Что касается величины db, то она является диагональю прямоугольника со сторонами a и b. Для нее можно записать следующие равенства:
db2 = a2 + b2 =>
b = √(db2 - a2)
Подставляя в последнее равенство найденное выражение для a, получим:
b = √(db2 - da2/2 )
Теперь можно подставить полученные формулы в выражение для объема правильной фигуры:
V = a2*b = da2/2*√(db2 - da2/2)
Заменив da и db числами из условия задачи, приходим к ответу: V ≈ 1304 см3.