Одним из важных вопросов при изучении термодинамических систем в физике является вопрос о возможности выполнения этой системой некоторой полезной работы. С концепцией работы тесно связано понятие внутренней энергии. В данной статье рассмотрим, что такое внутренняя энергия идеального газа, и приведем формулы для ее вычисления.
Идеальный газ
О газе, как агрегатном состоянии, не обладающем никакой силой упругости при внешнем воздействии на него и, как следствие, не сохраняющим объем и форму, знает каждый школьник. Концепция же газа идеального для многих остается непонятной и неясной. Объясним ее.
 Вам будет интересно:Список исчезающих народов мира
Вам будет интересно:Список исчезающих народов мира
Идеальным называется любой газ, который удовлетворяет следующим двум важным условиям:
- Составляющие его частицы не имеют размера. В действительности они имеют размер, но он настолько мал в сравнении с расстояниями между ними, что его можно не учитывать во всех математических расчетах.
- Частицы не взаимодействуют друг с другом с помощью сил Ван-дер-Ваальса или сил иной природы. На самом деле во всех реальных газах такое взаимодействие присутствует, но его энергия пренебрежимо мала по сравнению со средней энергией кинетической частиц.
Описанным условиям удовлетворяют практически все реальные газы, температуры которых лежат выше 300 К, а давления не превышают одной атмосферы. Для слишком высоких давлений и низких температур наблюдает отклонение газов от идеального поведения. В таком случае говорят о реальных газах. Они описываются уравнением Ван-дер-Ваальса.
Понятие о внутренней энергии идеального газа
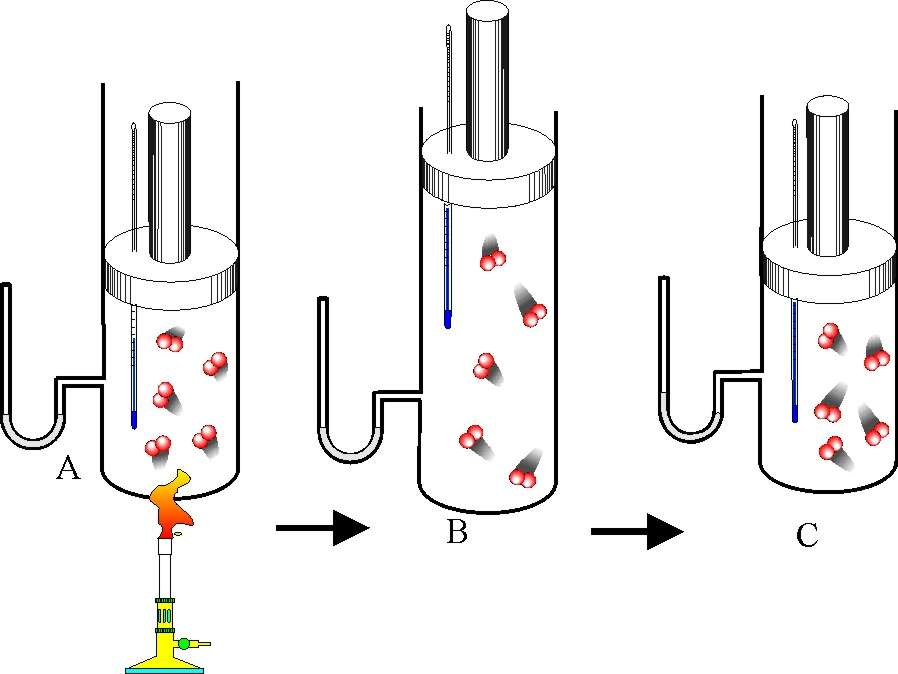
В соответствии с определением, под внутренней энергией системы понимают сумму кинетической и потенциальной энергий, заключенных внутри этой системы. Если применить эту концепцию к газу идеальному, то следует отбросить потенциальную составляющую. Действительно, поскольку частицы идеального газа не взаимодействуют друг с другом, то их можно считать движущимися свободно в абсолютном вакууме. Чтобы извлечь одну частицу из изучаемой системы, не нужно совершать работу против внутренних сил взаимодействия, поскольку этих сил не существует.
Таким образом, внутренняя энергия идеального газа всегда совпадает с его кинетической энергией. Последняя, в свою очередь, однозначно определяется молярной массой частиц системы, их количеством, а также средней скоростью поступательного и вращательного движения. Скорость движения зависит от температуры. Увеличение температуры приводит к увеличению внутренней энергии, и наоборот.
Формула для внутренней энергии
Обозначим внутреннюю энергию идеальной газовой системы буквой U. Согласно термодинамике, она определяется как разность энтальпии H системы и произведения давления на объем, то есть:
U = H - p*V.
В пункте выше мы выяснили, что величина U соответствует суммарной кинетической энергии Ek всех частиц газа:
U = Ek.
Из статистической механики в рамках положений молекулярно-кинетической теории (МКТ) идеального газа следует, что средняя кинетическая энергия одной частицы Ek1 равна следующей величине:
Ek1 = z/2*kB*T.
Здесь kB и T - постоянная Больцмана и температура, z - число степеней свободы. Полную кинетическую энергию системы Ek можно получить, если умножить Ek1 на количество частиц N в системе:
Ek = N*Ek1 = z/2*N*kB*T.
Таким образом, мы получили формулу для внутренней энергии идеального газа, записанную в общем виде через абсолютную температуру и число частиц в закрытой системе:
U = z/2*N*kB*T.
Одноатомный и многоатомный газ
Записанная в предыдущем пункте статьи формула для U является неудобной для ее практического использования, поскольку количество частиц N определить трудно. Тем не менее, если учесть определение количества вещества n, то это выражение можно переписать в более удобной форме:
n = N/NA; R = NA*kB = 8,314 Дж/(моль*К);
U = z/2*n*R *T.
Число степеней свободы z зависит от геометрии составляющих газ частиц. Так, для моноатомного газа z = 3, поскольку атом может независимо двигаться только в трех направлениях пространства. Если же газ является двухатомным, то z = 5, так как к трем поступательным степеням свободы добавляются еще две вращательные. Наконец, для любого другого многоатомного газа z = 6 (3 поступательные и 3 вращательные степени свободы). С учетом сказанного, можно записать в следующем виде формулы внутренней энергии идеального газа одноатомного, двухатомного и многоатомного:
U1 = 3/2*n*R*T;
U2 = 5/2*n*R*T;
U≥3 = 3*n*R*T.
Пример задачи на определение внутренней энергии
В баллоне объемом 100 литров находится чистый водород под давлением 3 атмосферы. Полагая водород идеальным газом при данных условиях, необходимо определить, чему равна его внутренняя энергия.

В записанных выше формулах для U присутствует количество вещества и температура газа. В условии же задачи совершенно ничего об этих величинах не сказано. Чтобы решить задачу, необходимо вспомнить универсальное уравнение Клапейрона-Менделеева. Оно имеет показанный на рисунке вид.
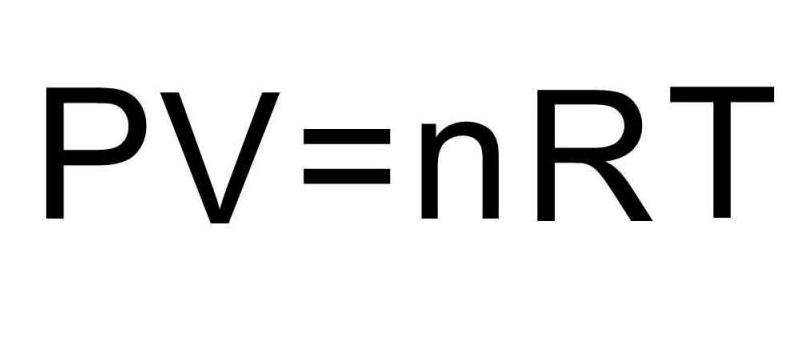
Поскольку водород H2 является двухатомной молекулой, то формула для внутренней энергии запишется в виде:
UH2 = 5/2*n*R*T.
Сравнивая оба выражения, приходим к конечной формуле для решения задачи:
UH2 = 5/2*P*V.
Остается перевести единицы давления и объема из условия в систему единиц СИ, подставить соответствующие значения в формулу для UH2 и получить ответ: UH2 ≈ 76 кДж.
