Геометрическая оптика является особым разделом оптики физической, которая не занимается природой света, а изучает законы движения световых лучей в прозрачных средах. Рассмотрим подробнее эти законы в статье, а также приведем примеры их использования для практики.
Распространение луча в однородном пространстве: важные свойства
Все знают, что свет является электромагнитной волной, которая для некоторых природных феноменов может вести себя как поток квантов энергии (явления фотоэффекта и светового давления). Геометрическая оптика, как было отмечено во введении, занимается только законами распространения света, не вникая в их природу.
 Вам будет интересно:Горючие вещества и их характеристики
Вам будет интересно:Горючие вещества и их характеристики
Если луч движется в однородной прозрачной среде или в вакууме и не встречает на своем пути никакого препятствия, тогда ход светового луча будет наблюдаться по прямой линии. Эта особенность привела к формулированию в середине XVII века французом Пьером Ферма принципа наименьшего времени (принцип Ферма).
Еще одной важной особенностью световых лучей является их независимость. Это означает, что каждый луч распространяется в пространстве, "не чувствуя" другого луча, не взаимодействуя с ним.
Наконец, третьим свойством света является изменение скорости его распространения при переходе из одного прозрачного материала в другой.
Отмеченные 3 свойства световых лучей используются при выводе законов отражения и преломления.
Явление отражения
Это физическое явление возникает, когда световой луч падает на непрозрачное препятствие, размер которого намного больше длины волны света. Факт отражения заключается в резком изменении траектории луча в одной и той же среде.
Предположим, что тонкий пучок света падает на непрозрачную плоскость под углом θ1 к нормали N, проведенной к данной плоскости через точку падения на нее луча. Затем луч отражается под некоторым углом θ2 к той же нормали N. Явление отражения подчиняется двум главным законам:
Применение явления отражения в геометрической оптике
Законы отражения светового луча используются при построении изображений объектов (реальных или мнимых) в зеркалах различной геометрии. Наиболее распространенными геометриями зеркал являются следующие:
- плоское зеркало;
- вогнутое;
- выпуклое.
В любом из них построить изображение достаточно просто. В плоском зеркале оно получается всегда мнимым, имеет тот же размер, что и сам объект, является прямым, в нем левая и правая стороны меняются местами.
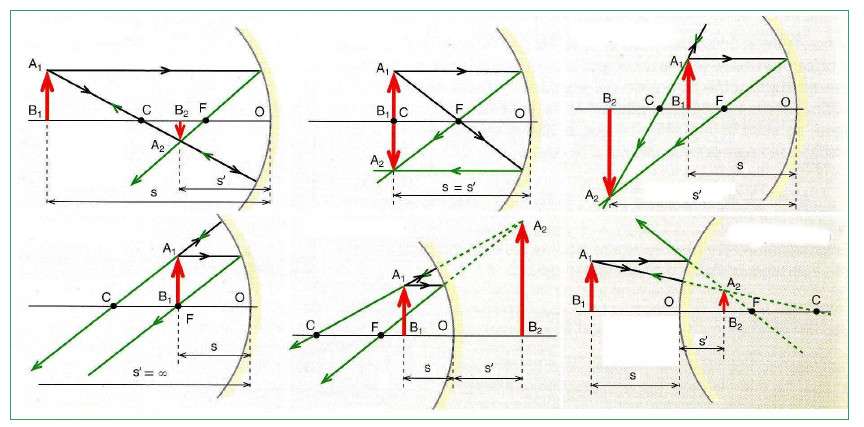
Изображения в вогнутом и в выпуклом зеркалах строятся с использованием нескольких лучей (параллельный оптической оси, проходящий через фокус и через центр). Тип их зависит от расстояния объекта до зеркала. Ниже приведен рисунок, где продемонстрировано, как строить изображения в выпуклых и вогнутых зеркалах.
Явление преломления
Оно состоит в изломе (преломлении) луча, когда он пересекает границу двух разных прозрачных сред (например, вода и воздух) под углом к поверхности, не равным 90o.
Современное математическое описание этого явления было сделано голландцем Снеллом и французом Декартом в начале XVII века. Обозначая углы θ1 и θ3 для падающего и преломленного лучей относительно нормали N к плоскости, запишем математическое выражение для явления преломления:
n1*sin(θ1) = n2*sin(θ3).
Величины n2 и n1 являют собой показатели преломления сред 2 и 1. Они показывают, как сильно скорость света в среде отличается от таковой в безвоздушном пространстве. Например, для воды n = 1,33, а для воздуха - 1,00029. Следует знать, что величина n является функцией частоты света (для больших частот n больше, чем для меньших).
Применение явления преломления в геометрической оптике
Описанное явление используется для построения изображений в тонких линзах. Линза - это объект, изготовленный из прозрачного материала (стекло, пластик и другие), который ограничен двумя поверхностями, причем как минимум одна из них имеет ненулевую кривизну. Линзы бывают двух видов:
- собирающие;
- рассеивающие.
Собирающие линзы образованы выпуклой сферической (сферическими) поверхностью. Преломление световых лучей в них происходит таким образом, что все параллельные лучи они собирают в одну точку - фокус. Рассеивающие образованы вогнутыми прозрачными поверхностями, поэтому после прохождения параллельных лучей через них происходит рассеивание света.
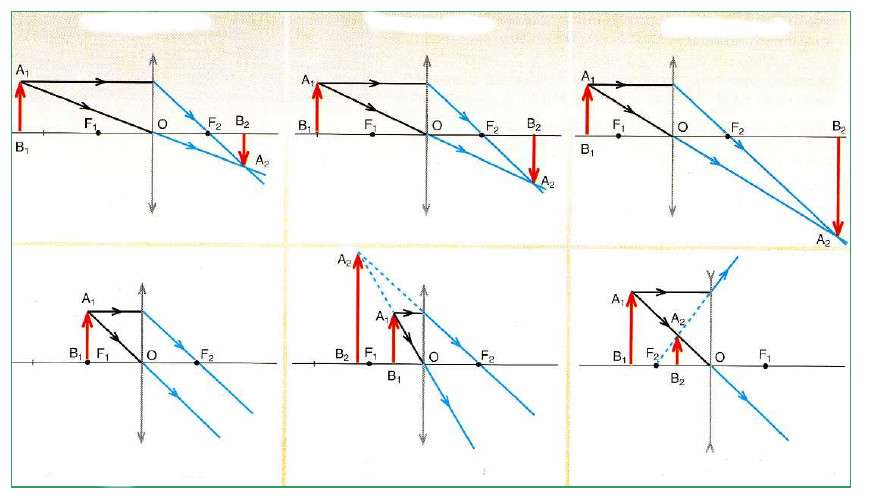
Построение изображений в линзах по своей технике подобно построению изображений в сферических зеркалах. Также необходимо использовать несколько лучей (параллельный оптической оси, проходящий через фокус и через оптический центр линзы). Характер полученных изображений определяется типом линзы и расстоянием объекта до нее. Ниже приведен рисунок, где показана техника получения изображений объекта в тонких линзах для различных случаев.
Приборы, работающие по законам геометрической оптики
Самым простым из них является лупа. Она представляет собой одну выпуклую линзу, которая служит для увеличения реальных объектов до 5 раз.

Более сложным прибором, который используется также для увеличения объектов, является микроскоп. Он состоит уже из системы линз (минимум из 2 собирающих) и позволяет получать увеличение в несколько сотен раз.

Наконец, третий важный оптический прибор - это телескоп, используемый для наблюдения за небесными телами. Он может состоять как из системы линз, тогда его называют рефракционным, так и из системы зеркал - рефлекторный телескоп. Эти названия отражают принцип его работы (преломление или отражение).