Тригонометрия является одним из наиболее важных разделов алгебры и геометрии для изучения в средней школе. Эта наука берет свое начало еще со времен античной Греции. В средние века наиболее весомый вклад в изучение и применение на практике тригонометрии внесли страны Ближнего Востока, а также Индия.
Зачастую в процессе изучения нового материала учащиеся испытывают сложности в понимании новой терминологии, особенно если она никак не связана с уже полученными ранее знаниями. Однако важно осознавать важность усвоения базовых основ любой темы, ведь от этого, в первую очередь, зависит успешность дальнейшего обучения ребенка. В данной статье мы рассмотрим такой тригонометрический термин, как sin угла, с которого, можно сказать, и начинается вся тригонометрия.
Определение
 Вам будет интересно:Голицын Дмитрий Михайлович - история жизни и становления дипломата
Вам будет интересно:Голицын Дмитрий Михайлович - история жизни и становления дипломата
Рассмотрим геометрический смысл данной функции.
Для определения синуса используется соотношение сторон прямоугольного треугольника. Рассмотрим подробнее. Sin - это отношение противолежащего катета к гипотенузе такого треугольника.
Для облегченного понимания объясним определение с использованием вспомогательного рисунка:
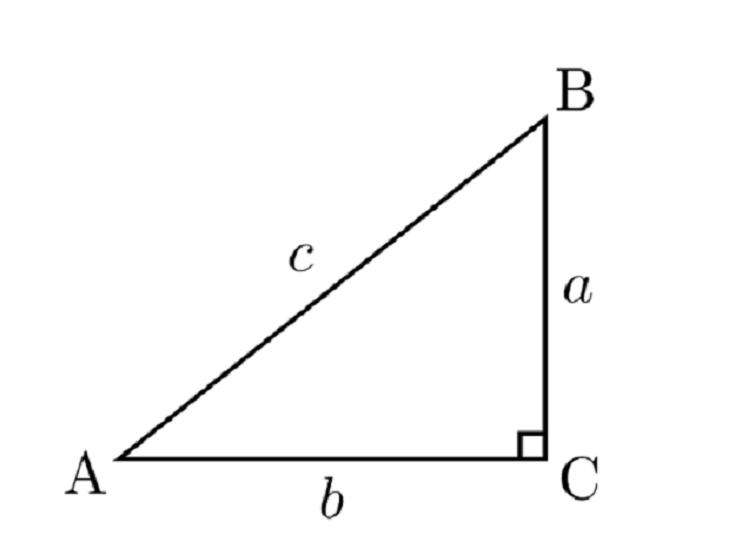
Применяя уже пройденные в геометрии термины, обозначим гипотенузу АВ маленькой латинской буквой с, а катеты прямоугольного треугольника АС и ВС примем за b и а соответственно. Таким образом, рассматривая угол А, его sin - это отношение a к с. Теперь рассмотрим другой, парный ему острый угол В. Его sin - это отношение b к с.
Теперь рассмотрим алгебраический смысл.
Если рассматривать термин "синус" с точки зрения этого раздела математики, то нам стоит обратиться к декартовой системе координат. Понадобится единичная окружность (радиус которой равен одной условной единице) с центром в начале координат.
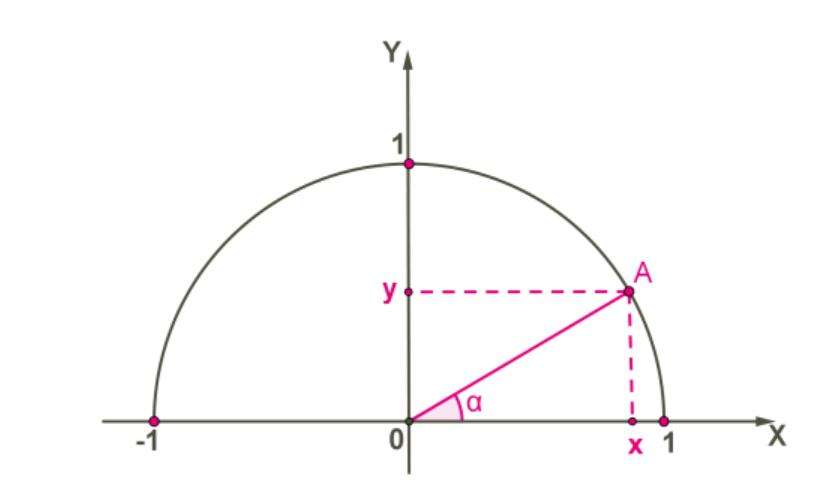
Отложим некий угол, равный альфа от оси абсцисс. Второй луч, образующий данный угол, пересекает единичную окружность в точке А. Она нам и потребуется, а именно ее вторая координата. Значение ее численно равно синусу отложенного угла.
Области определения и допустимых значений
Напоминаем общий случай. Область определения для функции принято обозначать как D(f), а находится она по оси абсцисс. В свою очередь область допустимых значений обозначается как E(f), а находить ее следует по оси ординат.
В нашем случае. Для синуса его область допустимых значений находится на отрезке от -1 до 1, а к области определения принадлежат все действительные числа. Также отметим, что функция синуса периодическая, а ее период равен пи.
Заключение
Теперь вы можете без толики сомнения ответить на все, связанные с определением sin угла вопросы, в том числе: sin - это отношение чего к чему, как он находится. Надеемся, что данная статья была полезной и понятной для вас.
