Изучение свойств газового агрегатного состояния материи является одним из важных направлений современной физики. Рассматривая газы в микроскопическом масштабе, можно получить все макроскопические параметры системы. В данной статье будет раскрыт важный вопрос молекулярно-кинетической теории газов: что собой представляет распределение Максвелла молекул по скоростям.
Исторический очерк
Идея о газе как системы, состоящей из микроскопических движущихся частиц, возникла еще в Античной Греции. Чтобы она получила свое развитие, науке понадобилось более 1700 лет.
Вам будет интересно:Матрицы: метод Гаусса. Вычисление матрицы методом Гаусса: примеры
Основоположником современной молекулярно-кинетической теории (МКТ) газа справедливо считать Даниила Бернулли. В 1738 году он опубликовал работу, которая называлась "Гидродинамика". В ней Бернулли изложил идеи МКТ, используемые до настоящего времени. Так, ученый полагал, что газы состоят из частиц, которые хаотически движутся во всех направлениях. Многочисленные соударения частиц со стенками сосудов воспринимаются, как наличие в газах давления. Скорости частиц тесно связаны с температурой системы. Сообщество ученых не приняло смелые идеи Бернулли, поскольку еще не был установлен закон сохранения энергии.
Впоследствии многие ученые занимались построением кинетической модели газов. Среди них следует отметить Рудольфа Клаузиуса, который в 1857 году создал простую газовую модель. В ней ученый уделил особое внимание наличию поступательных, вращательных и колебательных степеней свободы у молекул.
Вам будет интересно:Вглядитесь внимательно. Не попались ли среди встречных шедшие на вы?
В 1859 году, изучая работы Клаузиуса, Джеймс Максвелл сформулировал так называемое распределение Максвелла по скоростям молекул. По сути, Максвелл подтвердил идеи МКТ, подкрепив их математическим аппаратом. Впоследствии Людвиг Больцман (1871 год) обобщил выводы распределения Максвелла. Он постулировал более общее статистическое распределение молекул по скоростям и энергиям. Оно в настоящее время известно, как распределение Максвелла - Больцмана.
Идеальный газ. Основные постулаты МКТ
Чтобы понять, что собой представляет функция распределения Максвелла, необходимо четко разобраться с системами, для которых эта функция применима. Речь идет об идеальном газе. В физике под этой концепцией понимают текучую субстанцию, которая состоит из практически безразмерных частиц, не обладающих потенциальной энергией. Эти частицы движутся с большими скоростями, поэтому их поведение полностью определяется кинетической энергией. Более того, дистанции между частицами слишком велики по сравнению с их размерами, поэтому последними пренебрегают.
Вам будет интересно:Кляуза — это? Толкование слова
Идеальные газы описываются в рамках МКТ. Основными ее постулатами являются следующие:
- газовые системы состоят из огромного числа свободных частиц;
- частицы хаотически движутся с разными скоростями в разных направлениях по прямым траекториям;
- частицы сталкиваются со стенками сосудов упруго (вероятность столкновения частиц друг с другом невелика, ввиду их малых размеров);
- температура системы однозначно определяется средней кинетической энергией частиц, которая сохраняется во времени в случае установления в системе термодинамического равновесия.
Закон распределения Максвелла
Если бы человек обладал прибором, с помощью которого можно было измерить скорость отдельной молекулы газа, то, проведя соответствующий эксперимент, он был бы удивлен. Эксперимент бы показал, что каждая молекула любой газовой системы движется с совершенно произвольной скоростью. При этом в рамках одной системы, находящейся в тепловом равновесии с окружающей средой, были бы обнаружены как очень медленные, так и очень быстрые молекулы.
Закон распределения Максвелла по скоростям молекул газа представляет собой инструмент, позволяющий определить вероятность обнаружения частиц с заданной скоростью v в изучаемой системе. Соответствующая функция выглядит следующим образом:
f(v) = (m/(2*pi*k*T))3/2*4*pi*v2*exp(-m*v2/(2*k*T)).
В этом выражении m - масса частицы (молекулы), k - константа Больцмана, T - абсолютная температура. Таким образом, если известна химическая природа частиц (значение m), то функция f(v) однозначно определяется абсолютной температурой. Функция f(v) называется плотностью вероятности. Если взять от нее интеграл для некоторого предела скоростей (v; v+dv), то мы получим количество частиц Ni, которые имеют скорости в указанном промежутке. Соответственно, если взять интеграл от плотности вероятности f(v) для пределов скоростей от 0 до ∞, то мы получим полное число молекул N в системе.
Графическое изображение плотности вероятности f(v)
Функция плотности вероятности имеет несколько сложный математический вид, поэтому нелегко представить ее поведение при данной температуре. Эту задачу можно решить, если изобразить ее на двумерном графике. Схематический вид графика распределения Максвелла изображен ниже на рисунке.
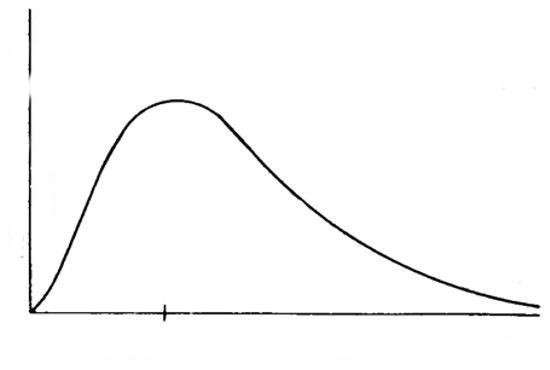
Мы видим, что он начинается с нуля, поскольку скорость v молекул не может иметь отрицательных значений. Заканчивается график где-то в области больших скоростей, плавно спадая до нуля (f(∞)->0). Также бросается в глаза следующая особенность: плавная кривая является несимметричной, она более резко убывает для небольших значений скоростей.
Важной особенностью поведения функции плотности вероятности f(v) является наличие на ней одного выраженного максимума. Согласно физическому смыслу функции, этот максимум соответствует наиболее вероятному значению скоростей молекул в газовой системе.
Важные виды скорости для функции f(v)
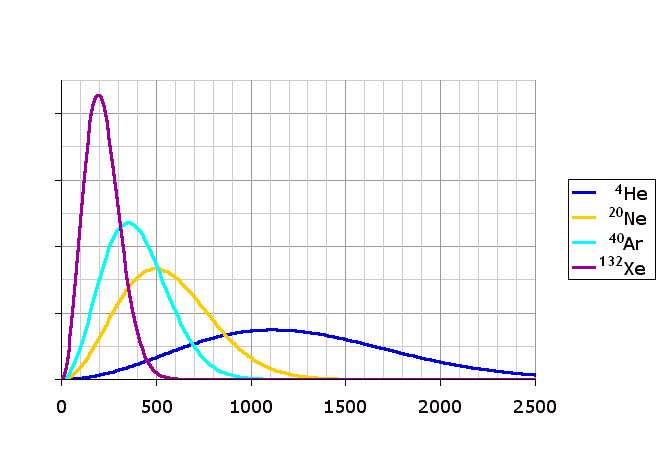
Функция плотности вероятности f(v) и ее графическое изображение позволяют дать определение трем важным видам скорости.
Первым видом скорости, который является очевидным, и который был упомянут выше, является наиболее вероятная скорость v1. На графике ее значение соответствует максимуму функции f(v). Именно эту скорость и близкие к ней значения будут иметь большинство частиц системы. Вычислить ее не представляет особого труда, для этого достаточно взять первую производную по скорости от функции f(v) и приравнять ее нулю. В результате проведения указанных математических операций получаем конечный результат:
v1 = √(2*R*T/M).
Здесь R - универсальная газовая постоянная, M - молярная масса молекул.
Вторым видом скорости является среднее ее значение для всех N частиц. Обозначим ее v2. Рассчитать ее можно, если проинтегрировать функцию v*f(v) по всем скоростям. Результатом отмеченного интегрирования будет следующая формула:
v2 = √(8*R*T/(pi*M)).
Поскольку отношение 8/pi>2, то средняя скорость всегда несколько больше, чем наиболее вероятная.
Каждый человек, который немного знаком с физикой, понимает, что средняя скорость v2 молекул должна иметь большое значение в газовой системе. Тем не менее это ошибочное суждение. Гораздо более важной является средняя квадратичная скорость. Обозначим ее v3.
Согласно определению, средняя квадратичная скорость является суммой квадратов индивидуальных скоростей всех частиц, деленная на число этих частиц, и взятая под квадратный корень. Рассчитать ее для распределения Максвелла можно, если определить интеграл по всем скоростям от функции v2*f(v). Формула для средней скорости квадратичной примет вид:
v3 = √(3*R*T/M).
Равенство показывает, что эта скорость больше, чем значения v2 и v1 для любой газовой системы.
Таким образом, все рассмотренные виды скоростей на графике распределения Максвелла лежат либо на экстремуме, либо правее его.
Важность величины v3
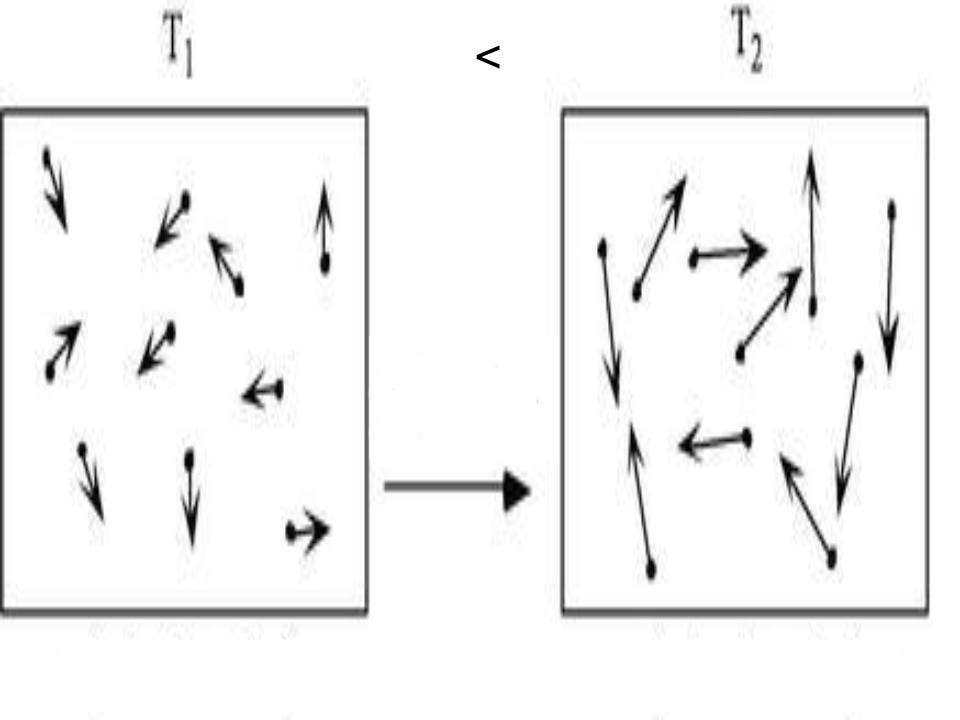
Выше было отмечено, что скорость средняя квадратичная является более важной для понимания физических процессов и свойств газовой системы, чем простая средняя скорость v2. Это действительно так, поскольку кинетическая энергия идеального газа зависит именно от величины v3, а не от v2.
Если рассматривать одноатомный идеальный газ, то для него справедливо следующее выражение:
m*v32/2 = 3/2*k*T.
Здесь каждая часть равенства представляет собой кинетическую энергию одной частицы массой m. Почему в выражении стоит именно величина v3, а не средняя скорость v2? Очень просто: при определении кинетической энергии каждой частицы ее индивидуальная скорость v возводится в квадрат, затем все скорости складываются и делятся на количество частиц N. То есть сама процедура определения кинетической энергии приводит к величине средней квадратичной скорости.
Зависимость функции f(v) от температуры
Выше мы установили, что плотность вероятности скоростей молекул однозначно зависит от температуры. Как будет изменяться функция, если увеличивать или уменьшать величину T? Ответить на этот вопрос поможет график ниже.
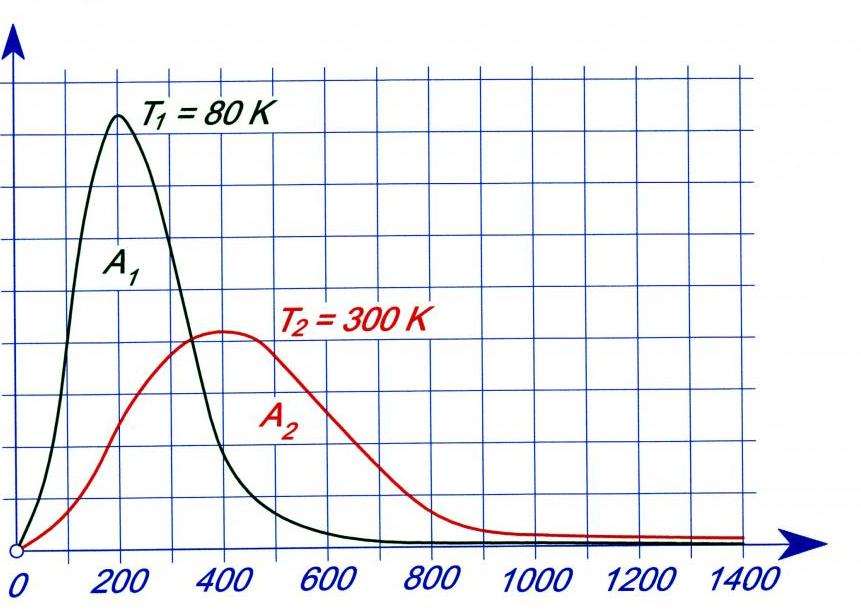
Видно, что нагрев закрытой системы приводит к размазыванию пика и его смещению в сторону более высоких скоростей. Увеличение температуры приводит к увеличению всех видов скоростей и к уменьшению плотности вероятности каждой из них. Значение пика уменьшается по причине сохранения количества частиц N в закрытой системе.
Далее, решим пару задач для закрепления полученного теоретического материала.
Задача с молекулами азота в воздухе
Необходимо рассчитать скорости v1, v2 и v3 для азота воздуха при температуре 300 К (около 27 oC).
Молярная масса азота N2 равна 28 г/моль. Пользуясь приведенными формулами, получаем:
v1 = √(2*R*T/M) = √(2*8,314*300/0,028) = 422 м/с;
v2 = √(8*R*T/(pi*M)) = √(8*8,314*300/(3,14*0,028)) = 476 м/с;
v3 = √(3*R*T/M) = √(3*8,314*300/0,028) = 517 м/с.
Задача с кислородом в баллоне
Кислород в баллоне находился при некоторой температуре T1. Затем баллон поместили в более холодное помещение. Как изменится график распределения Максвелла по скоростям для молекул кислорода, когда система придет в термодинамическое равновесие?
Вспоминая теорию, можно ответить так на вопрос задачи: значения всех видов скоростей молекул уменьшатся, пик функции f(v) сместится влево, станет более узким и более высоким.
