Кинетическая теория газов играет важную роль в понимании происходящих в газовых субстанциях процессов, которые тесно связаны с измеряемыми макроскопическими термодинамическими характеристиками системы. В приведенной ниже статье подробнее рассмотрим, что такое закон Максвелла и как с его помощью можно описать поведение идеальных газов.
Идеальные газы
Начнем статью с раскрытия вопроса, что такое идеальный газ. Под этим термином понимают такую текучую субстанцию, которая способна произвольным образом изменять свою форму и свой объем. Частицы, составляющие эту субстанцию, полагаются безразмерными и не взаимодействующими друг с другом. Безразмерными они считаются потому, что расстояние между ними намного больше их линейных размеров. Под отсутствием взаимодействия между частицами понимают их незначительную потенциальную энергию по сравнению с энергией кинетической поступательного и вращательного движения.
 Вам будет интересно:Генерал-губернатор Москвы Дмитрий Голицын
Вам будет интересно:Генерал-губернатор Москвы Дмитрий Голицын
Идеальные газы характеризуются низкими плотностями (давлениями), высокими абсолютными температурами и химической инертностью составляющих их молекул. Известным всем примером идеального газа является воздух на нашей планете.
Кинетическая теория и скорость движения молекул газа

Молекулярно-кинетическая теория (МКТ) является мощным инструментом, который из анализа статистических функций позволяет прогнозировать поведение макроскопических параметров системы таких, как температура, давление и объем. Основными положениями МКТ являются следующие:
- частицы, будь то атомы или молекулы, движутся хаотически по прямым траекториям;
- создаваемое давление обусловлено постоянными упругими столкновениями частиц со стенками содержащего газ сосуда;
- температура определяется средней кинетической энергией системы.
 Вам будет интересно:Идеальный одноатомный газ. Формула внутренней энергии. Решение задач
Вам будет интересно:Идеальный одноатомный газ. Формула внутренней энергии. Решение задач
Из этих постулатов МКТ, а также из ответа на вопрос, что такое идеальный газ, можно сделать важный вывод: скорость молекул v является ключевой микроскопической величиной, определяющей практически все свойства изучаемой системы.
Для полноты информации отметим, что МКТ получило свое развитие благодаря работам Бернулли, Ломоносова, Кренига и Клаузиуса. Во второй половине XIX века успех этой теории был обусловлен появлением статистического закона Максвелла о распределении скоростей газовых частиц. Впоследствии работы Максвелла были обобщены Больцманом на случай энергий частиц системы.
Функция плотности вероятности f(v)
Особенностью идеальных газов, находящихся в термодинамическом равновесии, является разнообразие скоростей составляющих их молекул. Действительно, если найти способ измерения индивидуальных скоростей, то можно обнаружить, что одни частицы движутся совсем медленно, другие же могут перемещаться быстрее. Этот интересный факт в 1873 году описал Максвелл, введя специальную функцию распределения молекул по скоростям. Эта функция называется вероятностью плотности, она имеет следующий вид:
f(v) = (m / (2 * pi * k * T))3/2 * 4 * pi * v2 * exp (-m * v2 / (2 * k * T)).
В этом выражении k, m и T - это постоянная Больцмана, масса частицы и абсолютная температура системы, соответственно. Плотность вероятности f(v) показывает вероятность обнаружения частиц со скоростями v ± dv в системе. Если взять интеграл от этой функции по всем скоростям, начиная от нуля и заканчивая бесконечностью, то мы получим полное число молекул N в изучаемой газовой системе.
График функции плотности вероятности
Математическая формула, приведенная выше в пункте, является несколько громоздкой и содержит степенную и показательную функции от температуры и массы частиц. Чтобы лучше понять ее свойства, представим эту функцию в графической форме.
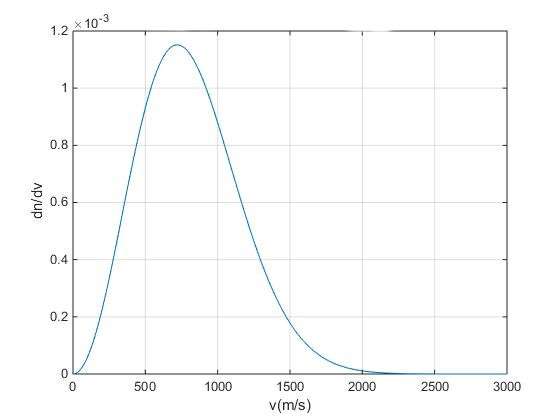
Видно, что закон Максвелла приводит к несимметричному распределению скоростей частиц. Кривая на графике обрывается относительно резко на малых скоростях и плавно спадает для больших значений v. Кривая имеет один максимум, который можно интерпретировать, как наиболее вероятную скорость молекул в системе.
Закон Максвелла подчиняется статистике Максвелла-Больцмана, область применения которой ограничивается только классической (ньютоновской) механикой. Как только частицы начинают проявлять квантовые свойства, следует пользоваться другими статистическими функциями для описания их поведения.
Вероятная, средняя и средняя квадратичная скорости
Распределение молекул по скоростям, которое описывает вероятность плотности f(v), позволяет рассчитать три важных вида скорости. Первым из них является наиболее вероятная скорость. Именно ее имеет в системе наибольшее число молекул. Рассчитывается она из равенства нулю производной df(v)/dv. Вероятная скорость v1 равна:
v1 = √(2 * R * T / M).
То есть она будет тем больше, чем выше температура газа, и чем меньше значение массы составляющих его частиц. Величина R здесь называется универсальной газовой постоянной.
Следующей скоростью является средняя величина. Ее рассчитывают при помощи интегрирования функции v * f(v) по всем скоростям. Результатом является средняя v2:
v2 = √(8 * R * T / (pi * M)).
Наконец, третьей важной скоростью является средняя квадратичная величина v3. Ее можно вычислить, если определить интеграл функции v2 * f(v) по всем скоростям молекул. Она равна:
v3 = √(3 * R * T / M).
Записанные три формулы показывают, что самой большой при любых температурах и массах молекул является средняя квадратичная величина. Она играет ключевую роль при вычислении кинетической энергии газа.
Скорость v3 и кинетическая энергия молекул
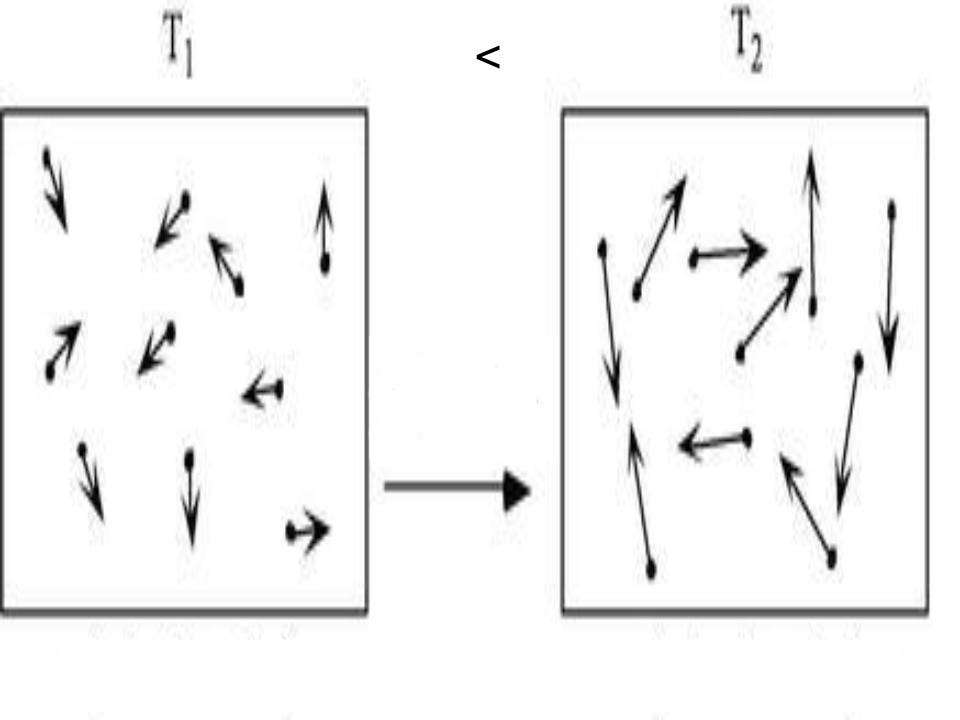
Поскольку в идеальных газах частицы друг с другом не взаимодействуют, то их внутренняя энергия состоит исключительно из кинетической. Из классической механики известно, что кинетическая энергия одной молекулы, которая движется со скоростью v и имеет массу m, вычисляется по формуле:
Ek = m * v2 / 2.
Очевидно, что складывая энергии Ek для всех N молекул системы, мы получим полную энергию идеального газа. Если разделить эту энергию на N, то получится средняя кинетическая энергия на одну молекулу. При этом соответствующая скорость будет средней квадратичной величиной v3. Для одноатомного газа, имеющего всего три поступательных степени свободы, справедлива следующая формула связи квадратичной скорости с температурой:
m * v32 / 2 = 3 / 2 * k * T.
Если вспомнить формулу связи между константами k и R, то можно получить ранее записанное выражение для v3 через абсолютную температуру.
Зависимость от температуры функции f(v)
Из закона Максвелла о распределении скоростей следует, что вероятность плотности f(v) зависит от величины T. Эту зависимость проще всего проследить на графике ниже.
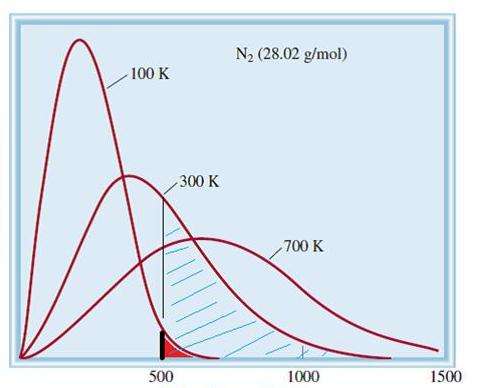
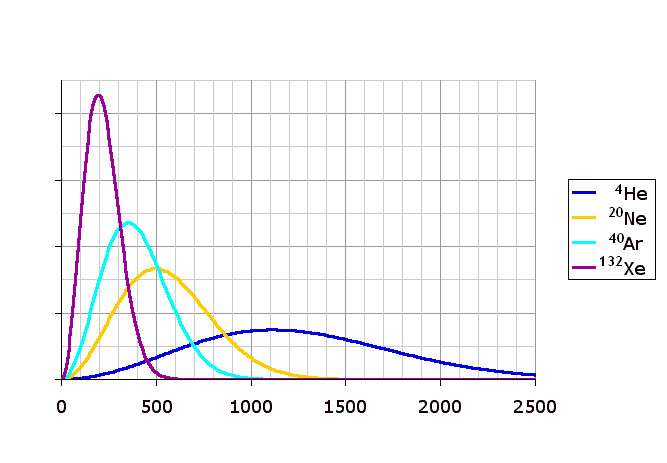
Увеличивая температуру от 100 К до 700 К для молекулярного азота, мы наблюдаем смещение пика вероятной скорости вправо. Кроме того, этот пик становится более размытым и уменьшается, что говорит о выравнивании скоростей молекул. Заметим, что площади под каждой из кривых остаются одинаковыми, поскольку число молекул азота в системе остается постоянным.
Пример задачи
Всем известны цветные резиновые шарики, которые наполняют гелием. Необходимо рассчитать вероятную, среднюю и среднюю квадратичную скорости для атомов гелия при комнатной температуре (298,15 К).

Молярная масса атома гелия составляет 4 г/моль. Используя это значение, получаем скорости v1, v2 и v3:
- v1 = √(2 * R * T / M) = √(2 * 8,314 * 298,15 / 0,004) = 1113 м/с;
- v2 = √(8 * R * T / (pi * M)) = √(8 * 8,314 * 298,15 / (3,14 * 0,004)) = 1257 м/с;
- v3 = √(3 * R * T / M) = √(3 * 8,314 * 298,15 / 0,004) = 1363 м/с.
Рассчитанные скорости свидетельствуют о том, что атомы гелия уже при комнатной температуре движутся в 3,5-4 раза быстрее скорости звука (≈340 м/с). При этом средняя квадратичная скорость атомов приблизительно на 20% превышает наиболее вероятную их скорость из распределения Максвелла.
