Ключом к успеху решения задач по физике является четкое понимание смысла величины, которую требуется найти. Знание конкретной формулы не является достаточным для решения практических задач, поскольку многие из них не предполагают использование определенной математической зависимости между величинами. Эту зависимость необходимо получить самостоятельно. В данной статье объясним, в чем состоит физический смысл ускорения.
Кинематика движения
Научный подход к изучению движения в физике стал применяться не так уж давно. В XVII, благодаря достижениям таких ученых, как Галилео Галилей и Исаак Ньютон, человечество, наконец, научилось предсказывать с использованием математического аппарата поведение тел во время их движения.
 Вам будет интересно:Показатели адиабаты: определение и процесс
Вам будет интересно:Показатели адиабаты: определение и процесс
Кинематика - это один из двух важных разделов физики (второй - динамика), который использует научный подход к описанию характеристик движения. В кинематике не заостряют внимание на причинах начала движения объектов. Ее основной задачей является определение координат тела в момент любой времени. Для решения этой задачи кинематика располагает набором характеристик, связанных в уравнения. Основными характеристиками являются путь пройденный, скорость и ускорение. Физический смысл последней величины рассмотрим далее в статье.
Определение ускорения

Как известно, быстрота прохождения пути описывается в физике скоростью. Если ее обозначить буквой v, а путь обозначить буквой l, можно записать тогда следующее выражение:
v = dl/dt.
Рассчитать модуль скорости в момент времени t просто, если найти производную по времени от функции l(t). Ускорение получается, если найти эту производную, но уже от функции v(t), то есть:
a = dv/dt.
Это равенство свидетельствует о том, что физический смысл ускорения состоит в быстроте изменения во времени скорости тела.
Ускорение - векторная характеристика
Скорость - это вектор, который направлен по касательной к линии, вдоль которой движется тело. Производная по времени от вектора - это также вектор, то есть ускорение векторной характеристикой является. Тем не менее, его направление не имеет ничего общего с вектором скорости v. Ускорение a направлено туда, куда и вектор изменения скорости. Например, в случае прямолинейного перемещения тел вектора величин a и v всегда будут лежать на одной прямой, поэтому существует два возможных варианта их взаимной ориентации:
- они направлены в одну сторону;
- они направлены противоположно друг другу.
В первом из названных случаев тело увеличивает свою скорость, то есть ускоряется. Во втором случае происходит торможение тела.
В случае криволинейного движения функция v(t) изменяется не только по модулю, но и по направлению. Ускорение описывает оба типа изменения скорости, поэтому его вектор направлен под некоторым углом к вектору величины v. Классическим примером является движение равномерное по окружности. Модуль скорости в этом случае остается постоянным, однако изменяется ее вектор. В результате соответствующее ускорение будет направлено к центру окружности. Оно называется нормальным или центростремительным.
Угловое ускорение
Выше был приведен пример равномерного движения по окружности. В общем же случае скорость движущегося тела изменяется по модулю в зависимости от времени. С этой целью в физике принято полное ускорение a раскладывать на тангенциальную at и на нормальную an компоненты. Первая описывает изменение скорости по величине, вторая - по направлению.
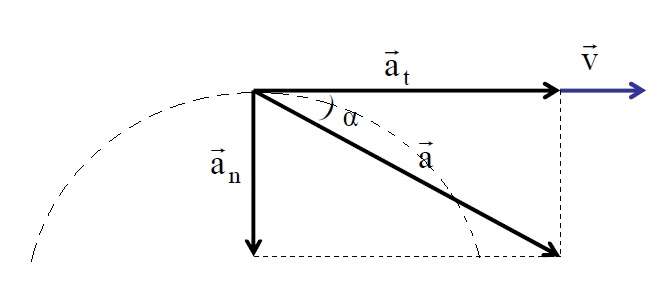
В случае ускоренного перемещения по окружности тело вращается вокруг оси. Для описания такого типа движения удобно использовать угловые кинематические характеристики: угол поворота θ, скорость угловую ω и угловое ускорение α. Эти величины связаны следующими равенствами:
ω = dθ/dt;
α = dω/dt.
Угловая скорость показывает, на какой в радианах угол тело поворачивается вокруг оси за одну секунду. Смысл физический углового ускорения заключается в том, что оно показывает, с какой скоростью изменяется величина ω. Например, если α = -1 рад/с2, то это означает, что скорость за каждую секунду уменьшается на 1 рад/с.
Угловые кинематические характеристики связаны с соответствующими линейными величинами следующими соотношениями:
v = ω*r;
at = α*r.
Оба равенства говорят об удобстве применения угловых величин для описания движения вращения. В отличие от линейных величин, они не зависят от радиуса r. Обращаем внимание, что угловое ускорение отлично от нуля только в том случае, если тело обладает некоторым тангенциальным ускорением.
Свободное падение

Под падением свободным в физике понимают только под действием силы тяжести движение тел. Эта сила вычисляется по следующей формуле:
F = m*g.
Здесь m - инерционная масса тела, g - постоянная величина вблизи поверхности планеты Земля. Она называется ускорением свободного падения. Физический смысл ускорения следующий: если тело падает свободно вертикально вниз, то за каждую секунду движения его скорость возрастать будет на 9,81 м/с. Наоборот, если брошено вверх вертикально тело, то скорость его за каждую секунду будет уменьшаться на величину g. Если начало движения тела осуществляется под некоторым углом к горизонту, то рассуждения выше справедливы только для вертикальной составляющей полной скорости.
