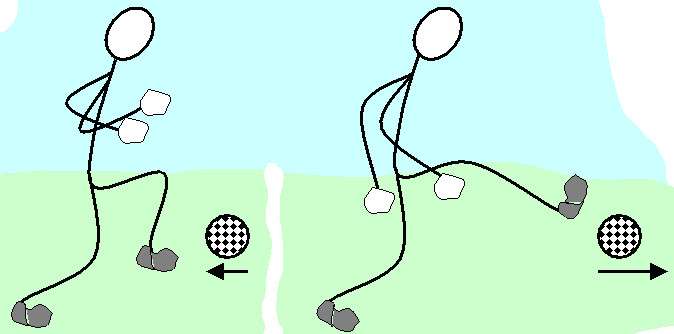
Количество движения, которое часто называют импульсом тела, является ключевой физической величиной в ньютоновской механике. Приведем в данной статье формулу импульса, объясним ее значение, а также рассмотрим другие величины и законы, связанные с ней.
Импульс тела и второй закон Ньютона
В начале XVII века Галилео Галилей, изучая законы механического движения тел, ввел в физику важную величину, которую он назвал количеством движения. Впоследствии Исаак Ньютон использовал достижения итальянского ученого при формулировке своих законов. Оба ученых под количеством движения понимали произведение инерционной массы тела на линейную скорость его перемещения в пространстве, то есть:
Вам будет интересно:В каком месте земная кора имеет наименьшую толщину: переходные зоны, океаническая и материковая кора
p¯ = m*v¯.
Величина p¯ является векторной, которая направлена точно так же, как скорость v¯. Физический смысл количества движения заключается в проявлении инерционных свойств тела и его кинетической энергии одновременно.
Если взять производную по времени от p¯, то мы получим второй ньютоновский закон:
dp¯/dt = m*dv¯/dt = m*a¯ = F¯.
Это равенство можно переписать в следующем виде:
dp¯ = F¯*dt.
Это выражение говорит о том, что действующая в течение времени dt сила F¯ приводит к изменению количества движения на величину dp¯. В правой части равенства стоит величина, которую называют импульсом силы. По этой причине выражение для количества движения p¯ стали называть формулой импульса.
Сохранение импульса
Важность изучаемой величины заключается в том, что она сохраняет свое значение в закрытых системах. Это означает, что если на тела системы действуют только внутренние силы, то количество движения между ними распределяется в результате внутренних взаимодействий, полный же импульс не изменяется с течением времени, то есть:
p¯ = const, если F¯ = 0.
Типичными видами взаимодействия являются столкновения тел, например, шаров. Столкновения могут быть абсолютно упругими, абсолютно пластичными или носить промежуточный характер. Тем не менее независимо от типа столкновения, суммарный импульс всегда сохраняется, что нельзя сказать о кинетической энергии. Она сохраняется только в случае упругих столкновений. При любом другом типе взаимодействия часть ее расходуется на нагрев тел, то есть переходит в тепловую энергию.
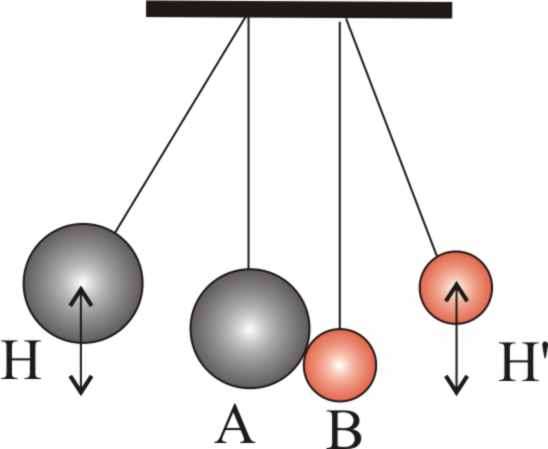
Когда решают задачи, то формулой сохранения импульса следует пользоваться покомпонентно, то есть в процессе внутренних взаимодействий тел каждый компонент суммарного импульса остается неизменным.
Момент импульса
Если рассмотренная выше величина p¯ характеризует линейное перемещение тела, то момент импульса L¯ - это свойство системы вращения. Для материальной точки массой m, вращающейся вокруг оси на расстоянии r со скоростью v, формула момента импульса имеет вид:
L¯ = [r¯*p¯] = [r¯*m*v¯].
Квадратные скобки указывают на векторное произведение. Направление L¯ перпендикулярно плоскости вращения точки и определяется по правилу руки правой.
Так же как и p¯, величина L¯ сохраняется, если отсутствуют внешние воздействия на систему (момент силы равен нулю). Если выражение выше дальше преобразовывать, используя угловую скорость ω¯ и момент инерции I, то закон сохранения момента импульса запишется в виде:
L¯ = I*ω¯ = const.
В действии этот закон можно наблюдать, когда фигурист вращается на льду, группируя различным образом свое тело.
Пример задачи с шарами
Используя формулу импульса, зная о законе его сохранения, решим такую задачу. Предположим, что два шара одинаковой массы m летят друг на друга. Скорость первого шара составляет v1, второго - v2. Необходимо определить скорость шаров после столкновения, зная, что v1 = 2*v2. Удар можно считать абсолютно неупругим.
После столкновения два шара будут двигаться как единое тело, поэтому справедлива следующая формула импульса:
m*v1 - m*v2 = 2*m*u.
За положительное направление скорости выбрано направление полета первого шара. Выражая отсюда u, и подставляя равенство v1 = 2*v2, получаем:
u = 1/2*(v1 - v2) = v2/2.
Таким образом, после столкновения два тела будут двигаться в сторону движения первого тела со скоростью v2/2.