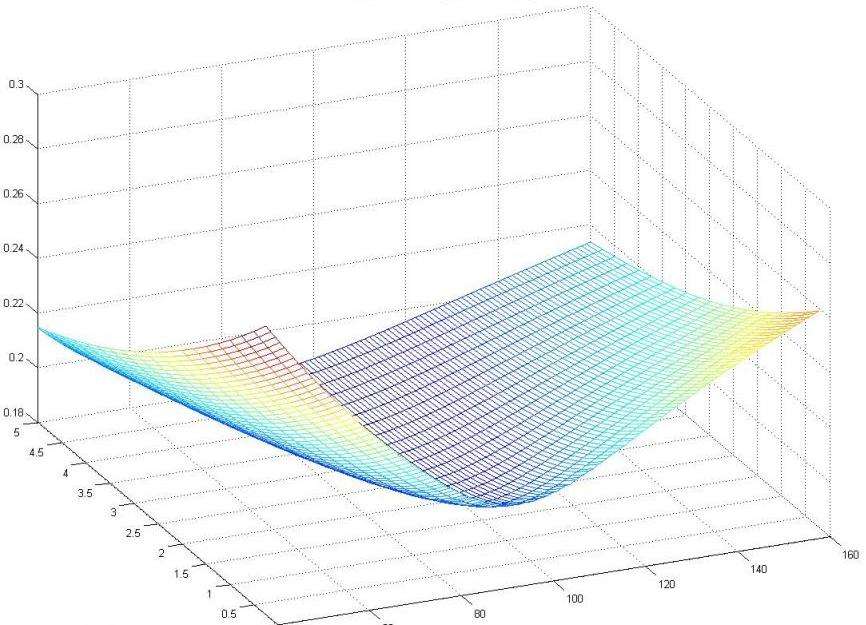
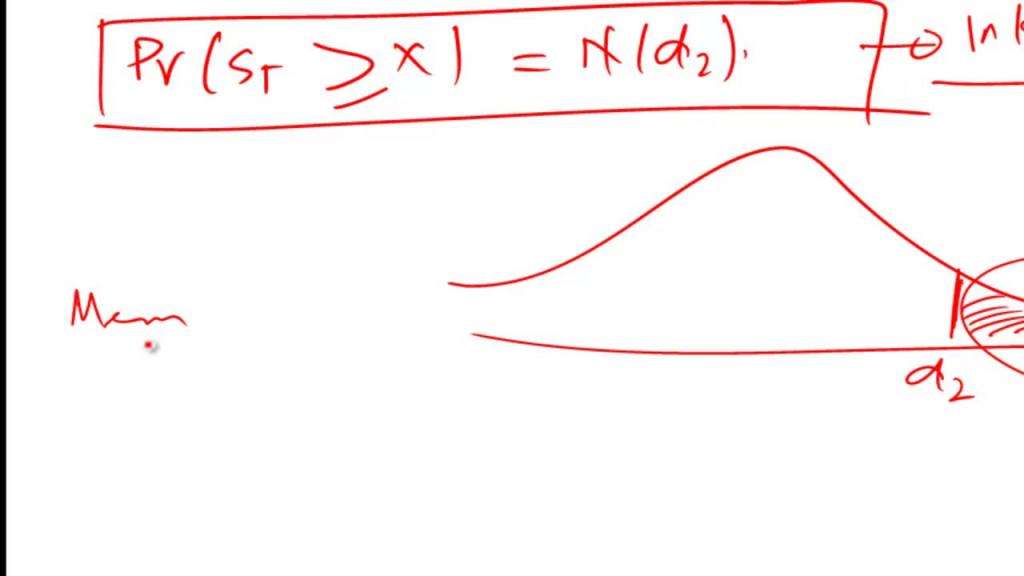В этой статье будет объяснена формула Блэка-Шоулза простыми словами. Модель Блэка-Шоулза представляет собой математическую модель динамики финансового рынка, содержащего производные инвестиционные инструменты.
Из уравнения с частными производными в модели (известной как уравнение Блэка-Шоулза) можно вывести формулу Блэка-Шоулза. Она дает теоретическую оценку цены опционов в европейском стиле и показывает, что опцион имеет уникальную цену независимо от риска ценной бумаги и ее ожидаемый доход (вместо замены ожидаемой доходности ценной бумаги на нейтральную к риску ставку).
 Вам будет интересно:Определение закона сохранения импульса. Формула и пример задачи. Закон сохранения момента импульса
Вам будет интересно:Определение закона сохранения импульса. Формула и пример задачи. Закон сохранения момента импульса
Формула привела к буму в торговле опционами и обеспечила математическую легитимность деятельности Чикагской биржи опционов и других опционных рынков по всему миру. Она широко используется, хотя часто с корректировками и исправлениями, участниками рынка опционов. На картинках в этой статье вы можете увидеть примеры формулы Блэка-Шоулза.
 Вам будет интересно:Расчет мощности двигателя: методики и необходимые формулы
Вам будет интересно:Расчет мощности двигателя: методики и необходимые формулы
История и суть
Основываясь на работах, ранее разработанных исследователями и практиками рынка, такими как Луи Бачелье, Шин Кассуф и Эд Торп, Фишер Блэк и Мирон Шоулз в конце 1960-х годов продемонстрировали, что динамический пересмотр портфеля устраняет ожидаемый возврат безопасности.
В 1970 году, после того, как они попытались применить формулу к рынкам и понесли финансовые потери из-за отсутствия управления рисками в своих профессиях, они решили сосредоточиться в своей области, академической среде. После трехлетних усилий формула, названная в честь их обнародования, была, наконец, опубликована в 1973 году в статье, озаглавленной «Ценообразование опционов и корпоративных обязательств», в Журнале политической экономии. Роберт С. Мертон был первым, кто опубликовал статью, расширяющую математическое понимание модели ценообразования опционов, и ввел термин «модель ценообразования Блэка – Шоулза».
 Вам будет интересно:Момент инерции материальной точки и твердого тела: формулы, теорема Штейнера, пример решения задачи
Вам будет интересно:Момент инерции материальной точки и твердого тела: формулы, теорема Штейнера, пример решения задачи
За свою работу Мертон и Шоулз получили Нобелевскую мемориальную премию по экономическим наукам 1997 года, комитет, сославшись на то, что они открыли динамический пересмотр, не зависящий от риска, как прорыв, который отделяет вариант от риска базовой безопасности. Несмотря на то, что он не получил награду из-за своей смерти в 1995 году, Шведский академик упомянул Блэка как участника. На картинке ниже вы можете увидеть типичную формулу расчету Блэка-Шоулза.
Опционы
Основная идея этой модели заключается в хеджировании опциона путем правильной покупки и продажи базового актива и, как следствие, устранения риска. Этот тип подстраховки называется «постоянно обновляемым дельта-хеджированием». Он является основой более сложных стратегий, таких как те, которые используются инвестиционными банками и хедж-фондами.
Управление рисками
Предположения модели были смягчены и обобщены во многих направлениях, что привело к множеству моделей, которые в настоящее время используются в ценообразовании производных инструментов и управлении рисками. Именно понимание модели, как показано в формуле Блэка-Шоулза, часто используется участниками рынка, в отличие от фактических цен. Эти сведения включают в себя отсутствие арбитражных границ и ценообразование, не зависящее от риска (благодаря постоянному пересмотру). Кроме того, уравнение Блэка-Шоулза, уравнение в частных производных, которое определяет цену опциона, позволяет определять цены с помощью численных методов, когда явная формула невозможна.
Волатильность
Формула Блэка-Шоулза имеет только один параметр, который нельзя непосредственно наблюдать на рынке: средняя будущая волатильность базового актива, хотя ее можно найти по цене других опционов. Поскольку значение параметра (будь то «положил» или «вызов») увеличивается в этом параметре, его можно инвертировать, чтобы получить «поверхность волатильности», которая затем используется для калибровки других моделей, например, внебиржевых деривативов.
С учетом этих предположений предположим, что на этом рынке также торгуются производные ценные бумаги. Мы указываем, что эта ценная бумага будет иметь определенную выплату на определенную дату в будущем, в зависимости от стоимости, принятой акцией до этой даты. Удивительно, что цена производного инструмента полностью определена в настоящее время, хотя мы не знаем, по какому пути пойдет цена акций в будущем.
Для особого случая европейского опциона "колл" или "пут" Блэк и Шоулз показали, что возможно создать хеджируемую позицию, состоящую из длинной позиции в акции и короткой позиции в опционе, значение которой не будет зависеть от цены акции. Их стратегия динамического хеджирования привела к уравнению в частных производных, которое определяло цену опциона. Его решение дается формулой Блэка-Шоулза.
Разность слагаемых
Формулу Блэка-Шоулза для excel можно интерпретировать, сначала разбив опцион "колл" на разницу двух бинарных опционов. Опцион "колл" обменивает денежные средства на актив по истечении срока, в то время как колл-актив с активом или без него просто дает актив (без наличных денег в обмен), а "колл" с безналичным расчетом просто возвращает деньги (без обмена актива). Формула Блэка-Шоулза для опциона представляет собой разность двух слагаемых, и эти два слагаемых равны значению опций двоичного вызова. Эти бинарные опционы продаются гораздо реже, чем ванильные опционы, но их легче анализировать.
На практике некоторые значения чувствительности обычно приводятся в сокращенном выражении, чтобы соответствовать шкале вероятных изменений параметров. Например, часто сообщается о rho, деленном на 10000 (изменение на 1 базисный пункт), vega на 100 (изменение на 1 объемный пункт) и тета на 365 или 252 (1-дневный спад на основе либо календарных дней, либо торговых дней в году).
Описанная выше модель может быть расширена для переменных (но детерминированных) ставок и волатильности. Модель также может быть использована для оценки европейских опционов на инструменты выплаты дивидендов. В этом случае доступны решения в закрытой форме, если дивиденд является известной пропорцией цены акции. Американские опционы и опционы на акции, выплачивающие известный денежный дивиденд (в краткосрочной перспективе, более реалистичный, чем пропорциональный дивиденд), сложнее оценить, и доступен выбор методов решения (например, решеток и сеток).
Приближение
Полезное приближение: хотя волатильность не постоянна, результаты модели часто помогают установить хеджирование в правильных пропорциях для минимизации риска. Даже если результаты не совсем точны, они служат первым приближением, к которому можно вносить корректировки.

Основа для более совершенных моделей: модель Блэка-Шоулза является надежной в том смысле, что ее можно отрегулировать, чтобы справиться с некоторыми из ее отказов. Вместо того, чтобы рассматривать некоторые параметры (такие как волатильность или процентные ставки) как постоянные, мы рассматриваем их как переменные и, таким образом, добавляем источники риска.
Это отражается на греках (изменение значения опции для изменения этих параметров или эквивалентно частным производным по этим переменным), и хеджирование этих греков снижает риск, вызванный непостоянной природой этих параметров. Однако другие дефекты не могут быть устранены путем изменения модели, в частности, хвостового риска и риска ликвидности, и вместо этого они управляются вне модели, главным образом путем минимизации этих рисков и стресс-тестирования.
Явное моделирование
Явное моделирование: эта функция означает, что вместо того, чтобы предполагать волатильность априори и вычислять цены из нее, можно использовать модель для определения волатильности, которая дает подразумеваемую волатильность опциона по заданным ценам, срокам и ценам исполнения. Решая волатильность в течение определенного набора продолжительности и цен страйка, можно построить поверхность подразумеваемой волатильности.
В этом приложении модели Блэка-Шоулза получено преобразование координат из области цен в область волатильности. Вместо того чтобы указывать цены опционов в долларах за единицу (которые трудно сравнивать по страйкам, длительностям и частоте купонов), цены опционов могут быть указаны в терминах подразумеваемой волатильности, что ведет к торговле волатильностью на рынках опционов.