Начало всему положили греки. Не нынешние, а те, что жили раньше. Калькуляторов еще не было, а потребности в вычислениях уже присутствовали. И почти любое вычисление приводило в конечном итоге к прямоугольным треугольникам. Они дали решение многих проблем, одна из которых звучала так: "Как найти гипотенузу, зная угол и катет?".
Треугольники с прямым углом
Несмотря на простоту определения, эта фигура на плоскости может задать немало загадок. Многие испытали это на себе, хотя бы в школьной программе. Хорошо еще, что на все вопросы он сам же и дает ответы.
Вам будет интересно:Хлорид кальция и карбонат кальция: химические свойства
Но нельзя ли еще упростить это несложное сочетание сторон и углов? Оказалось, можно. Достаточно сделать один угол прямым, т. е. равным 90°.
Казалось бы, какая разница? Огромная. Если во всем многообразии углов разобраться почти невозможно, то, зафиксировав один из них, легко прийти к удивительным выводам. Что и сделал Пифагор.
Он ли придумал слова "катет" и "гипотенуза" или это сделал кто-то другой — неважно. Главное, что они получили имена не просто так, а благодаря своим отношениям с прямым углом. Две стороны прилегали к нему. Это и были катеты. Третья противолежала, она стала гипотенузой.
И что с того?
Хотя бы то, что появилась возможность ответить на вопрос, как найти гипотенузу по катету и углу. Благодаря понятиям, введенным древним греком, стали возможными логические построения отношений сторон и углов.
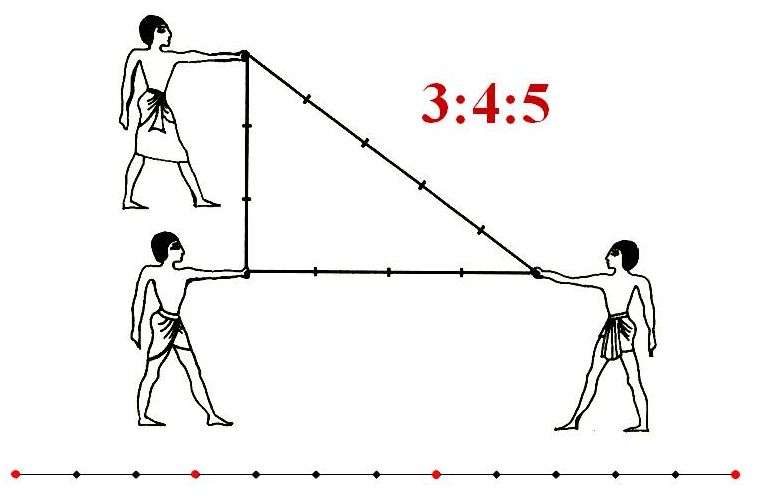
Сами-то треугольники, прямоугольные в том числе, использовались еще при строительстве пирамид. Знаменитый египетский треугольник со сторонами 3, 4 и 5, возможно, подтолкнул Пифагора к формулированию знаменитой теоремы. Она, в свою очередь, стала решением проблемы, как найти гипотенузу, зная угол и катет
Квадраты сторон оказались взаимно связанными друг с другом. Заслуга древнего грека не в том, что он это заметил, а в том, что сумел доказать свою теорему для всех других треугольников, а не только египетского.
Теперь стало легко вычислить длину одной стороны, зная две другие. Но в жизни большей частью возникают задачи другого рода, когда надо узнать гипотенузу, зная катет и угол. Как определить ширину реки, не замочив ног? Легко. Строим треугольник, один катет которого и есть ширина реки, другой нам известен по построению. Знать бы еще противолежащую сторону... Решение нашли уже последователи Пифагора.
Итак, задача: как найти гипотенузу, зная угол и катет
Кроме отношений квадратов сторон они обнаружили еще множество других любопытных отношений. Для их описания ввели новые определения: синус, косинус, тангенс, котангенс и прочую тригонометрию. Обозначения для формул были такими: Sin, Cos, Tg, Ctg. Что это такое, показано на рисунке.
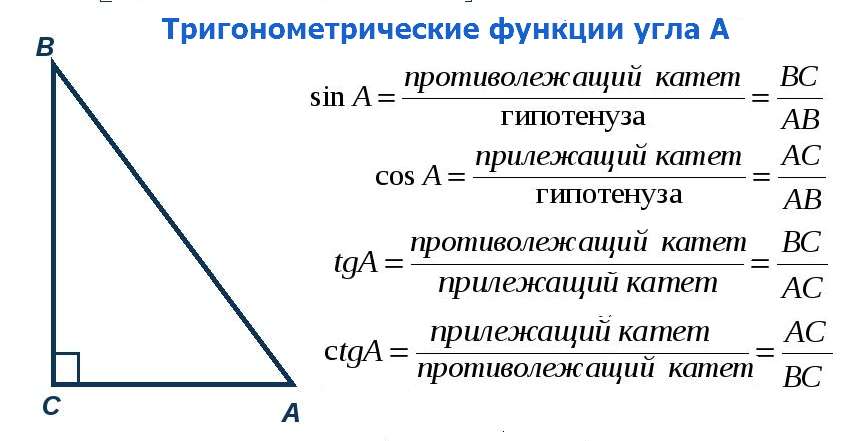
Значения функций, если известен угол, давно вычислены и сведены в таблицы знаменитым русским ученым Брадисом. Например, Sin30° = 0,5. И так для каждого угла. Вернемся теперь к реке, на одном берегу которой мы провели линию СА. Ее длина нам известна: 30 метров. Сами же проводили. На противоположной стороне стоит дерево в точке В. Измерить угол А трудов не составит, пусть это будет 60°.
В таблице синусов находим значение для угла 60° - это 0,866. Значит, СААВ = 0,866. Поэтому АВ определится как СА:0,866 = 34,64. Теперь, когда известны 2 стороны прямоугольного треугольника, вычислить третью труда не составит. Пифагор все сделал за нас, надо только подставить цифры:
ВС = √АВ2 - AC2 = √1199,93 - 900 = √299,93 = 17,32 метра.
Вот так мы убили двух зайцев одним выстрелом: выяснили, как найти гипотенузу, зная угол и катет, и вычислили ширину реки.