Одними из распространенных в стереометрии являются задачи на пересечение прямых линий и плоскостей и на вычисление углов между ними. Рассмотрим в данной статье подробнее так называемый координатный метод и углы между прямой и плоскостью.
Прямая и плоскость в геометрии
Прежде чем рассматривать координатный метод и угол между прямой и плоскостью, следует познакомиться с названными геометрическими объектами.
Прямой называется такая совокупность точек в пространстве или на плоскости, каждая из которых может быть получена линейным переносом предыдущей на определенный вектор. Далее будем обозначать этот вектор символом u¯. Если этот вектор умножить на любое число, которое не равно нулю, то мы получим параллельный u¯ вектор. Прямая - это линейный бесконечный объект.
 Вам будет интересно:Что значит "присно" - понятие и синонимы
Вам будет интересно:Что значит "присно" - понятие и синонимы
Плоскость - это также совокупность точек, которые расположены таким образом, что если из них составлять произвольные вектора, то все они будут перпендикулярны некоторому вектору n¯. Последний называют нормальным или просто нормалью. Плоскость, в отличие от прямой, является двумерным бесконечным объектом.
Координатный метод решения задач по геометрии
Исходя из названия самого метода, можно сделать вывод, что речь идет о способе решения задач, который основан на выполнении аналитических последовательных расчетов. Иными словами, координатный метод позволяет решать геометрические проблемы с использованием универсальных инструментов алгебры, главным из которых являются уравнения.
 Вам будет интересно:Молвить — это устаревший глагол: толкование и синонимы
Вам будет интересно:Молвить — это устаревший глагол: толкование и синонимы
Следует отметить, что рассматриваемый метод появился на заре зарождения современных геометрии и алгебры. Большой вклад в его развитие внесли Рене Декарт, Пьер Ферма, Исаак Ньютон и Лейбниц в XVII-XVIII века.
Суть метода заключается в проведении вычислений расстояний, углов, площадей и объемов геометрических элементов, основываясь на координатах известных точек. Заметим, что форма полученных итоговых уравнений зависит от системы координат. Чаще всего в задачах применяют прямоугольную декартову систему, поскольку с ней удобнее всего работать.
Уравнение прямой
Рассмотрение координатного метода и углов между прямой и плоскостью начнем с задания уравнения прямой. Существует несколько способов представления в алгебраической форме прямых. Здесь рассмотрим только векторное уравнение, поскольку из него можно легко получить любую другую форму и с ним легко работать.
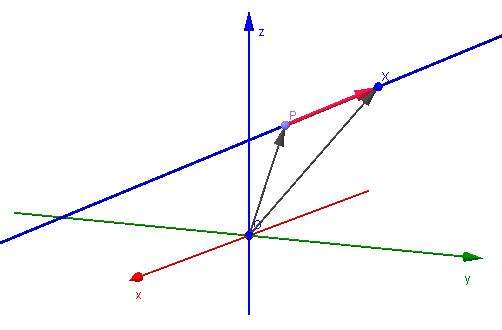
Предположим, что имеются две точки: P и Q. Известно, что через них можно провести прямую, причем она будет единственной. Соответствующее математическое представление элемента выглядит так:
(x, y, z) = P + λ*PQ¯.
Где PQ¯ - это вектор, координаты которого получают следующим образом:
PQ¯ = Q - P.
Символом λ обозначен параметр, который может принимать абсолютно любое число.
В записанном выражении можно изменять направление вектора, а также вместо точки P подставить координаты Q. Все эти преобразования не приведут к изменению геометрического расположения прямой.
Отметим, что при решении задач иногда требуется представлять в явном (параметрическом) виде записанное векторное уравнение.
Задание плоскости в пространстве
Так же как и для прямой, существует для плоскости тоже несколько форм математических уравнений. Среди них отметим векторное, уравнение в отрезках и общего вида. В данной статье уделим особое внимание именно последней форме.
Уравнение общего вида для произвольной плоскости может быть записано таким образом:
A*x + B*y + C*z + D = 0.
Латинские большие буквы - это определенные числа, задающие плоскость.
Удобство этой формы записи заключается в том, что в ней в явном виде содержится нормальный к плоскости вектор. Он равен:
n¯ = (A, B, C).
Знание этого вектора позволяет, взглянув бегло на уравнение плоскости, представить расположение последней в координатной системе.
Взаимное расположение в пространстве прямой и плоскости
В следующем пункте статьи мы перейдем к рассмотрению координатного метода и угла между прямой и плоскостью. Здесь же ответим на вопрос, каким образом в пространстве могут располагаться рассматриваемые геометрические элементы. Существует три таких способа:
Во втором и третьем случаях угол между указанными геометрическими объектами равен нулю. В первом же случае он лежит в пределах от 0 до 90o.
Вычисление углов между прямыми и плоскостями
Теперь перейдем непосредственно к теме статьи. Любое пересечение прямой и плоскости происходит под некоторым углом. Этот угол образован самой прямой и ее проекцией на плоскость. Проекцию можно получить, если из любой точки прямой опустить на плоскость перпендикуляр, а затем через полученную точку пересечения плоскости и перпендикуляра и точку пересечения плоскости и исходной прямой провести прямую, которая будет проекцией.
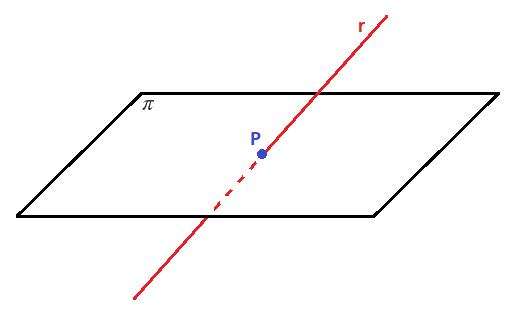
Вычисление углов между прямыми и плоскостями не представляет собой сложной задачи. Для ее решения достаточно знать уравнения соответствующих геометрических объектов. Допустим, эти уравнения выглядят следующим образом:
(x, y, z) = (x0, y0, z0) + λ*(a, b, c);
A*x + B*y + C*z + D = 0.
Искомый угол легко находится, если воспользоваться свойством произведение скалярного векторов u¯ и n¯. Конечная формула выглядит так:
θ = arcsin(|(u¯*n¯)|/(|u¯|*|n¯|)).
Эта формула говорит о том, что синус угла между прямой и плоскостью равен отношению модуля скалярного произведения отмеченных векторов к произведению их длин. Чтобы понять, почему вместо косинуса появился синус, обратимся к рисунку ниже.
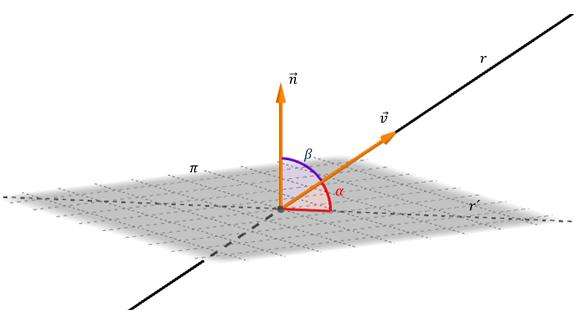
Видно, что если мы применим функцию косинуса, то мы получим угол между векторами u¯ и n¯. Искомый же угол θ (α на рисунке) получается так:
θ = 90o - β.
Синус появляется в результате применения формул приведения.
Пример задачи
Перейдем к практическому использованию полученных знаний. Решим типичную задачу на угол между прямой и плоскостью. Заданы следующие координаты четырех точек:
P = (1, -1, 0);
Q = (-1, 2, 2);
M = (0, 3, -1);
N = (-2, -1, 1).
Известно, что через точки PQM проходит плоскость, а через MN - прямая. Используя координатный метод, угол между плоскостью и прямой необходимо рассчитать.
Для начала запишем уравнения прямой и плоскости. Для прямой его составить несложно:
MN¯ = (-2, -4, 2) =>
(x, y, z) = (0, 3, -1) + λ*(-2, -4, 2).
Чтобы составить уравнение плоскости, найдем сначала нормаль к ней. Ее координаты равны векторному произведению двух векторов, лежащих в данной плоскости. Имеем:
PQ¯ = (-2, 3, 2);
QM¯ = (1, 1, -3) =>
n¯ = [PQ¯*QM¯] = (-11, -4, -5).
Теперь в уравнение общее плоскости подставим координаты любой лежащей в ней точки, чтобы получить значение свободного члена D:
P = (1, -1, 0);
- (A*x + B*y + C*z) = D =>
D = - (-11 + 4 + 0) = 7.
Уравнение плоскости имеет вид:
11*x + 4*y + 5*z - 7 = 0.
Осталось применить формулу для угла, образующегося при пересечении прямой и плоскости, чтобы получить ответ на задачу. Имеем:
(u¯*n¯) = (11, 4, 5)*(-2, -4, 2) = -28;
|u¯| = √24; |n¯| = √162;
θ = arcsin(28/√(162*24)) = 26,68o.
На примере этой задачи мы показали, как использовать координатный метод для решения геометрических проблем.
