Призма является достаточно простой геометрической объемной фигурой. Тем не менее у некоторых школьников при определении ее основных свойств возникают проблемы, причина которых, как правило, связана с неправильно используемой терминологией. В данной статье рассмотрим, какие призмы бывают, как они называются, а также подробно охарактеризуем правильную четырехугольную призму.
Призма в геометрии
Изучение объемных фигур является задачей стереометрии - важной части пространственной геометрии. В стереометрии под призмой понимают такую фигуру, которая образована параллельным переносом произвольного плоского многоугольника на определенное расстояние в пространстве. Параллельный перенос предполагает такое перемещение, при котором поворот вокруг оси, перпендикулярной плоскости многоугольника, полностью исключен.
 Вам будет интересно:Холю и лелею. Что значит лелеять и холить?
Вам будет интересно:Холю и лелею. Что значит лелеять и холить?
В результате описанного способа получения призмы образуется фигура, ограниченная двумя многоугольниками, имеющими одинаковые размеры, лежащими в параллельных плоскостях, и некоторым числом параллелограммов. Их количество совпадает с числом сторон (вершин) многоугольника. Одинаковые многоугольники называются основаниями призмы, а площадь их поверхности - это площадь оснований. Параллелограммы, соединяющие два основания, образуют боковую поверхность.
Элементы призмы и теорема Эйлера
Поскольку рассматриваемая объемная фигура представляет собой полиэдр, то есть образована набором пересекающихся плоскостей, то она характеризуется некоторым количеством вершин, ребер и граней. Все они являются элементами призмы.
В середине XVIII века швейцарский математик Леонард Эйлер установил связь между количеством основных элементов полиэдра. Эта связь записывается следующей простой формулой:
Число ребер = число вершин + число граней - 2
Для любой призмы справедливо это равенство. Приведем пример его использования. Предположим, имеется правильная четырехугольная призма. Она изображена на рисунке ниже.
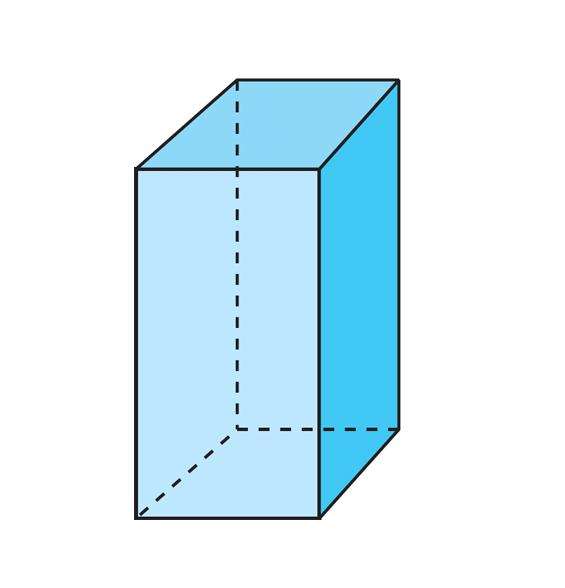
Видно, что число вершин для нее равно 8 (по 4 для каждого четырехугольного основания). Число сторон, или граней составляет 6 (2 основания и 4 боковых прямоугольника). Тогда количество ребер для нее будет равно:
Число ребер = 8 + 6 - 2 = 12
Все их можно посчитать, если обратится к тому же рисунку. Восемь ребер лежат в основаниях, а четыре ребра перпендикулярны этим основаниям.
Полная классификация призм
С этой классификацией важно разобраться, чтобы впоследствии не путаться в терминологии и использовать правильные формулы для вычисления, например, площади поверхности или объема фигур.
Для любой призмы произвольной формы можно выделить 4 признака, которые ее будут характеризовать. Перечислим их:
- По количеству углов многоугольника в основании: треугольная, пятиугольная, восьмиугольная и так далее.
- По типу многоугольника. Он может быть правильным или неправильным. Например, прямоугольный треугольник является неправильным, а равносторонний - правильным.
- По типу выпуклости многоугольника. Он может быть вогнутым или выпуклым. Чаще всего встречаются выпуклые призмы.
- По углам между основаниями и боковыми параллелограммами. Если все эти углы равны 90o, то говорят о прямой призме, если не все из них являются прямыми, то такую фигуру называют косоугольной.
Из всех этих пунктов хотелось бы остановиться подробнее на последнем. Прямая призма также называется прямоугольной. Связано это с тем, что для нее параллелограммы являются прямоугольниками в общем случае (в некоторых случаях они могут быть квадратами).
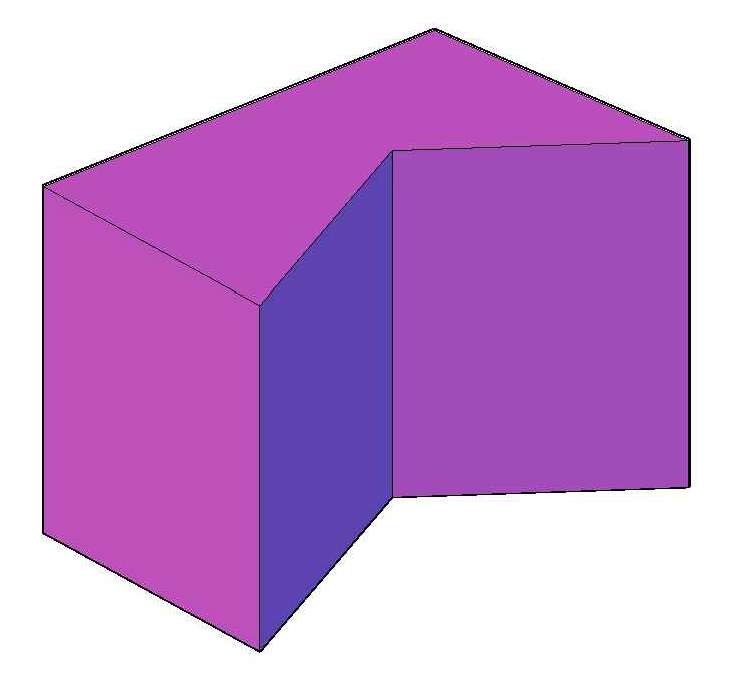
Для примера на рисунке выше изображена пятиугольная вогнутая прямоугольная, или прямая фигура.
Правильная четырехугольная призма
Основание этой призмы представляет собой правильный четырехугольник, то есть квадрат. Выше на рисунке уже было показано, как выглядит эта призма. Помимо двух квадратов, которые ее ограничивают сверху и снизу, она также включает 4 прямоугольника.
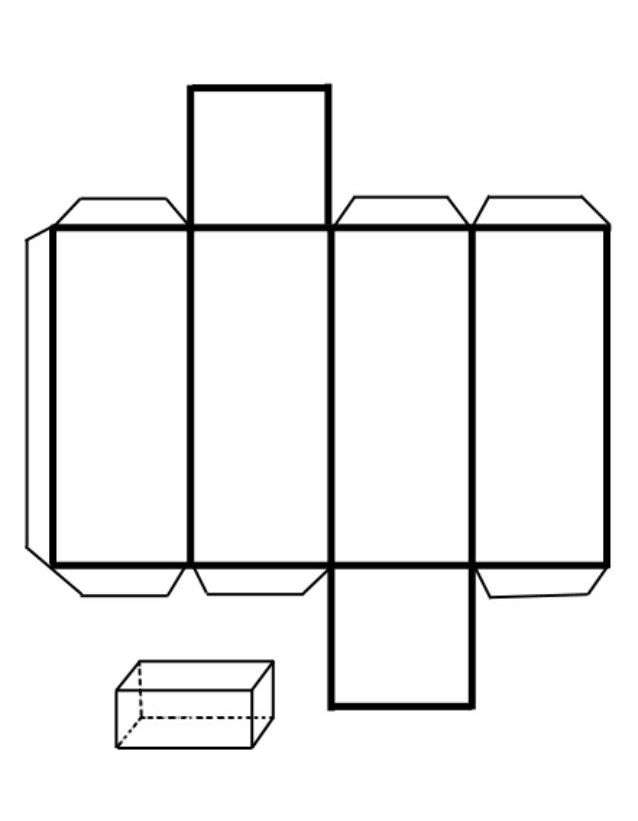
Обозначим сторону основания правильной четырехугольной призмы буквой a, длину ее бокового ребра обозначим буквой c. Эта длина также является высотой фигуры. Тогда площадь всей поверхности этой призмы выразится формулой:
S = 2*a2 + 4*a*c = 2*a*(a + 2*c)
Здесь первое слагаемое отражает вклад оснований в общую площадь, второе слагаемое - это площадь боковой поверхности.
Учитывая введенные обозначения для длин сторон, запишем формулу для объема рассматриваемой фигуры:
V = a2*c
То есть объем вычисляется как произведение площади квадратного основания на длину бокового ребра.
Фигура куб
Все знают эту идеальную объемную фигуру, но мало кто задумывался, что она представляет собой правильную четырехугольную призму, сторона которой равна длине стороны квадратного основания, то есть c = a.
Для куба формулы полной площади поверхности и объема примут вид:
S = 6*a2
V = a3
Поскольку куб - это призма, состоящая из 6 одинаковых квадратов, то любую параллельную пару из них можно считать основанием.
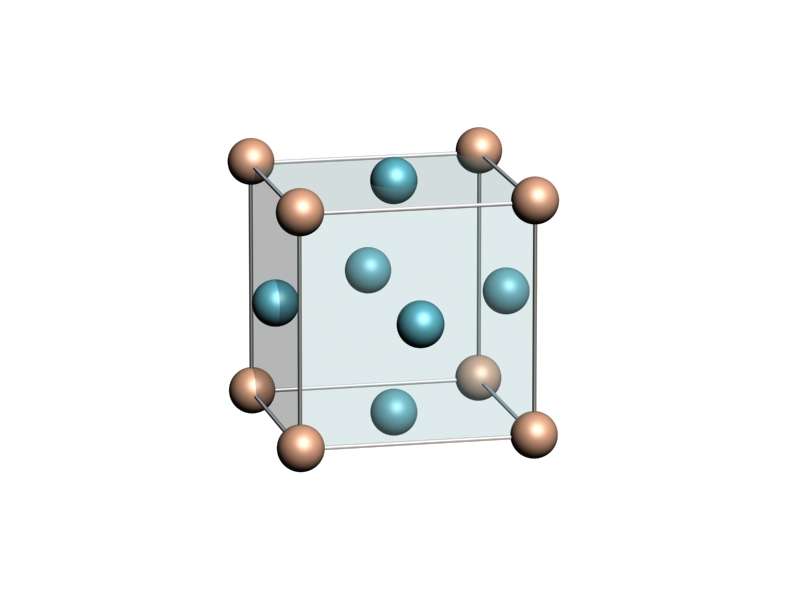
Куб - это высокосимметричная фигура, которая в природе реализуется в виде кристаллических решеток многих металлических материалов и ионных кристаллов. Например, решетки золота, серебра, меди и поваренной соли являются кубическими.
