Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная - это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.
 Вам будет интересно:Как написать письмо учителю? Образец письма учителю от ученика
Вам будет интересно:Как написать письмо учителю? Образец письма учителю от ученика
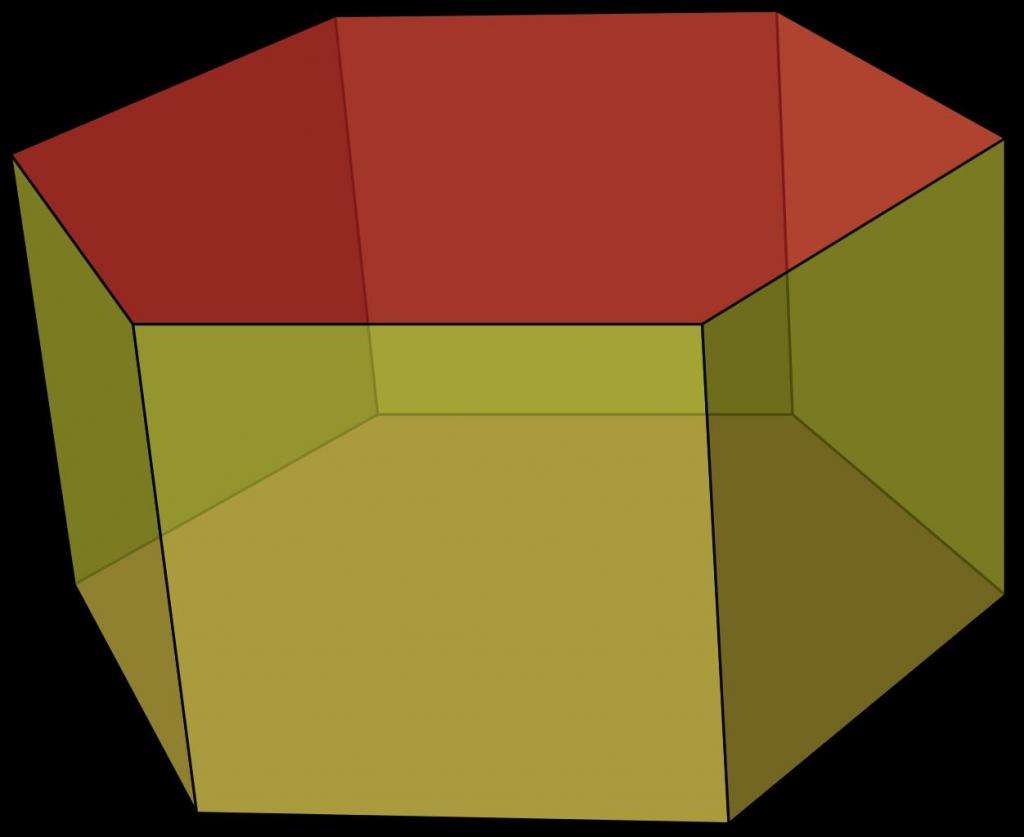
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90o. Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин - 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
Рисунок ниже показывает все эти диагонали.
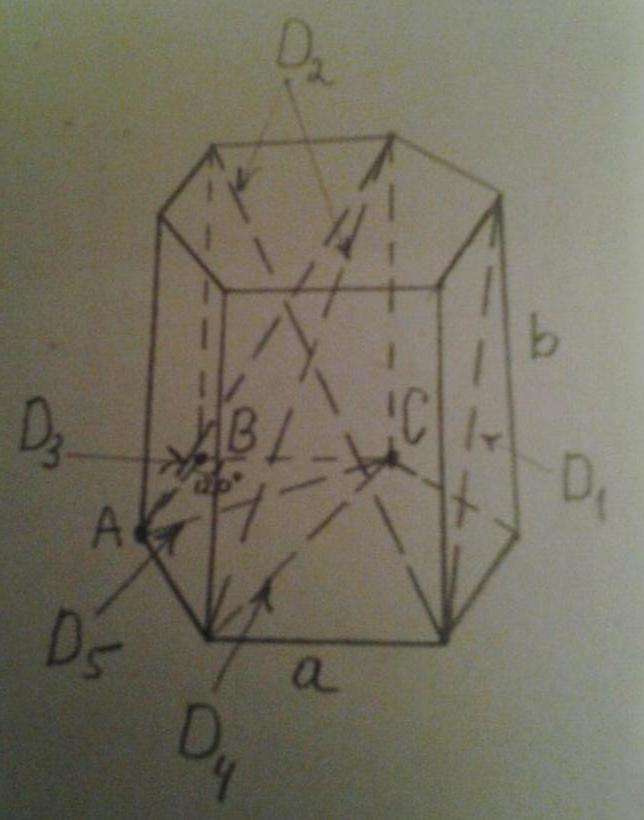
Видно, что D1 - это диагональ боковой стороны, D2 и D3 - диагонали всей призмы, D4 и D5 - диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b - длину бокового ребра. Тогда диагональ имеет длину:
D1 = √(a2 + b2).
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
D4 = 2*a.
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120o. Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
AC/2 = AB*sin(60o) = a*√3/2.
Сторона AC является диагональю D5, поэтому получаем:
D5 = AC = √3*a.
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
D2 = √(D42 + b2) = √(4*a2 + b2);
D3 = √(D52+ b2) = √(3*a2+ b2).
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
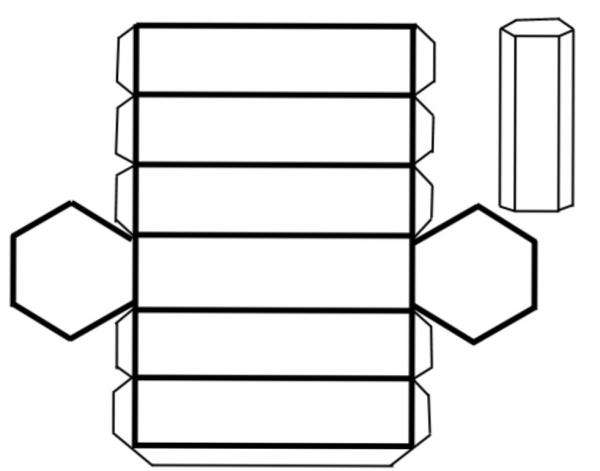
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
S1 = a*b.
Тогда площадь боковой поверхности равна:
S2 = 6*a*b.
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Sn = n/4*a2*ctg(pi/n).
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
S6 = 6/4*a2*ctg(pi/6) = 3*√3/2*a2.
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Sos = 3*√3*a2.
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
S = Sos + S2 = 3*√3*a2 + 6*a*b = 3*a*(√3*a + 2*b).
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
V = S6*b = 3*√3/2*a2*b.
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
