Векторы на плоскости и в пространстве: формулы и примеры

Вектор является важным геометрическим объектом, с помощью свойств которого удобно решать многие проблемы на плоскости и в пространстве. В данной статье дадим ему определение, рассмотрим его основные характеристики, а также покажем, как для задания плоскостей вектор в пространстве может быть использован.

Что такое вектор: двумерный случай

В первую очередь необходимо четко понимать, о каком объекте идет речь. В геометрии вектором называется направленный отрезок. Как и любой отрезок, он характеризуется двумя основными элементами: начальной и конечной точек. Координаты этих точек однозначно определяют все характеристики вектора.

Вам будет интересно:Совещание. Кто примет участие в совещании

Рассмотрим пример вектора на плоскости. Для этого проведем две взаимно перпендикулярные оси x и y. Отметим произвольную точку P(x, y). Если соединить эту точку с началом координат (точка O), а затем указать направление к P, тогда мы получим вектор OP¯ (далее в статье черта над символом показывает, что рассматривается вектор). Рисунок вектора на плоскости изображен ниже.

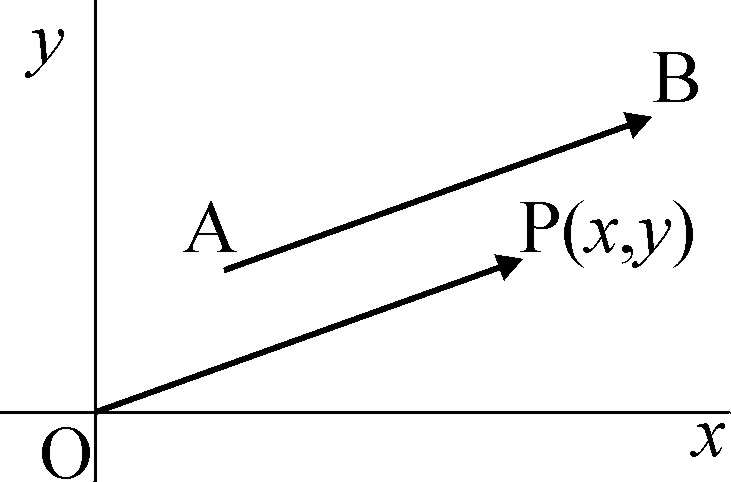
Здесь также изображен другой вектор AB¯, и видно, что его характеристики совершенно идентичны OP¯, однако он находится в другой части системы координат. Путем параллельного переноса OP¯ можно получить бесконечное количество векторов с одинаковыми свойствами.

Вектор в пространстве

Все реальные объекты, которые нас окружают, находятся в трехмерном пространстве. Изучением геометрических свойств трехмерных фигур занимается стереометрия, которая оперирует понятием трехмерных векторов. От двумерных они отличаются только тем, что для их описания необходима дополнительная координата, которая отсчитывается вдоль третьей перпендикулярной x и y оси z.

Рисунок ниже демонстрирует вектор в пространстве. Координаты его конца вдоль каждой оси обозначены цветными отрезками. Начало вектора находится в точке пересечения всех трех координатных осей, то есть имеет координаты (0; 0; 0).

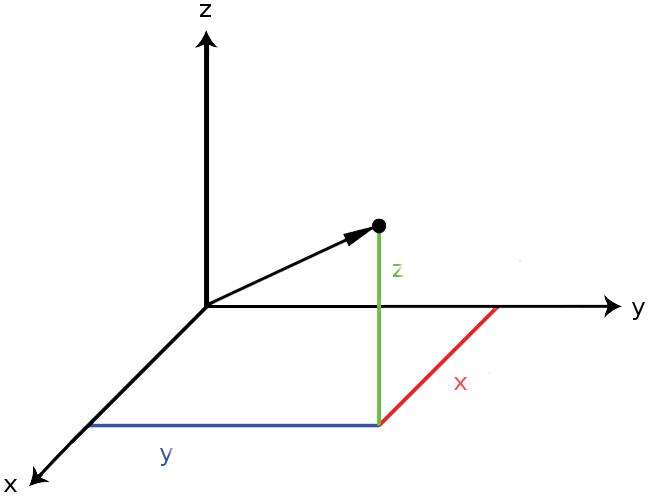
Поскольку вектор на плоскости является частным случаем пространственно направленного отрезка, то далее в статье будем рассматривать только трехмерный вектор.

Координаты вектора по известным координатам его начала и конца

Предположим, что имеется две точки P(x1; y1; z1) и Q(x2; y2; z2). Как определить координаты вектора PQ¯. Во-первых, следует условиться, какая из точек будет началом, а какая концом вектора. В математике принято записывать рассматриваемый объект вдоль его направления, то есть P - начало, Q - конец. Во-вторых, координаты вектора PQ¯ вычисляются как разности соответствующих координат конца и начала, то есть:

PQ¯ = (x2 - x1; y2 - y1; z2 - z1).

Отметим, что изменив направление вектора, его координаты поменяют знак, так:

QP¯ = (x1 - x2; y1 - y2; z1 - z2).

Это означает, что PQ¯ = -QP¯.

Важно понимать еще один момент. Выше было сказано, что в плоскости существует бесчисленное количество векторов, равных данному. Этот факт справедлив и для пространственного случая. По сути, когда мы вычисляли координаты PQ¯ в примере выше, мы осуществляли операцию параллельного переноса этого вектора таким образом, чтобы его начало совпало с началом координат. Вектор PQ¯ может быть изображен в виде направленного отрезка из начала координат в точку M((x2 - x1; y2 - y1; z2 - z1).

Свойства вектора

Как и любой объект геометрии, вектор имеет некоторые свойственные ему характеристики, которые можно использовать при решении задач. Кратко перечислим их.

Модуль вектора - это длина направленного отрезка. Зная координаты, вычислить ее просто. Для вектора PQ¯ в примере выше модуль равен:

|PQ¯| = √[(x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2].

Модуль вектора на плоскости рассчитывается по аналогичной формуле, только без участия третьей координаты.

Сумма и разность векторов осуществляется по правилу треугольника. Рисунок ниже показывает, как выполняются операции сложения и вычитания этих объектов.

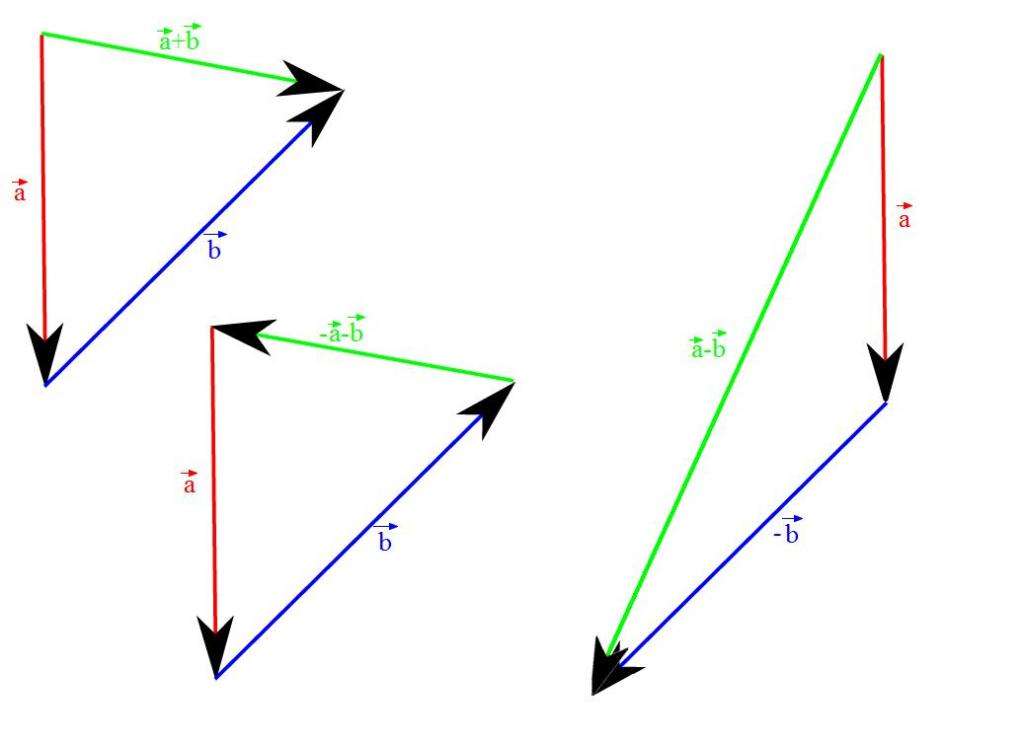
Чтобы получить вектор суммы, необходимо к концу первого вектора приложить начало второго. Искомый вектор будет начинаться в начале первого и заканчиваться на конце второго вектора.

Разность выполняется с учетом того, что вычитаемый вектор заменяется на противоположный, а затем проводится описанная выше операция сложения.

Помимо сложения и вычитания, важно уметь умножать вектор на число. Если число равно k, тогда получается вектор, модуль которого в k раз отличается от исходного, а направление либо совпадает (k>0), либо противоположно исходному (k<0).

Также определена операция умножения векторов между собой. Для нее выделим отдельный пункт в статье.

Скалярное и векторное умножение

Предположим, что имеются два вектора u¯(x1; y1; z1) и v¯(x2; y2; z2). Вектор на вектор можно умножить двумя различными способами:

Скалярное произведение векторов u¯ и v¯ рассчитывается так:

(u¯*v¯) = |u¯|*|v¯|*cos(α).

Где α - угол между данными векторами.

Можно показать, что зная координаты u¯ и v¯, их скалярное произведение можно вычислить по следующей формуле:

(u¯*v¯) = x1*x2 + y1*y2 + z1*z2.

Скалярное произведение удобно использовать при разложении вектора на два перпендикулярно направленных отрезка. Также его применяют для вычисления параллельности или ортогональности векторов, и для расчета угла между ними.

Векторное произведение u¯и v¯ дает новый вектор, который перпендикулярен исходным и имеет модуль:

[u¯*v¯] = |u¯|*|v¯|*sin(α).

Направление вниз или вверх нового вектора определяется по правилу правой руки (четыре пальца правой руки направлены от конца первого вектора к концу второго, а оттопыренный вверх большой палец указывает направление нового вектора). На рисунке ниже показан результат векторного произведения для произвольных a¯и b¯.

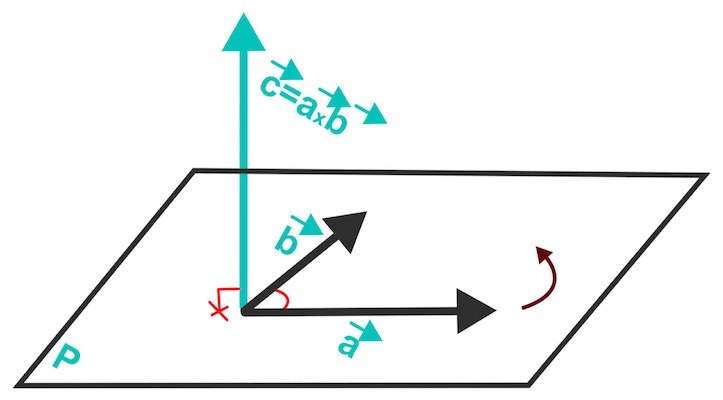
Векторное произведение применяется для вычисления площадей фигур, а также при определении координат вектора, перпендикулярного заданной плоскости.

Векторы и их свойства удобно использовать при определении уравнения плоскости.

Нормаль и общее уравнение плоскости

Определить плоскость можно несколькими способами. Одним из них является вывод общего уравнение плоскости, которое непосредственно следует из знания вектора, перпендикулярного ей, и некоторой известной точки, которая принадлежит плоскости.

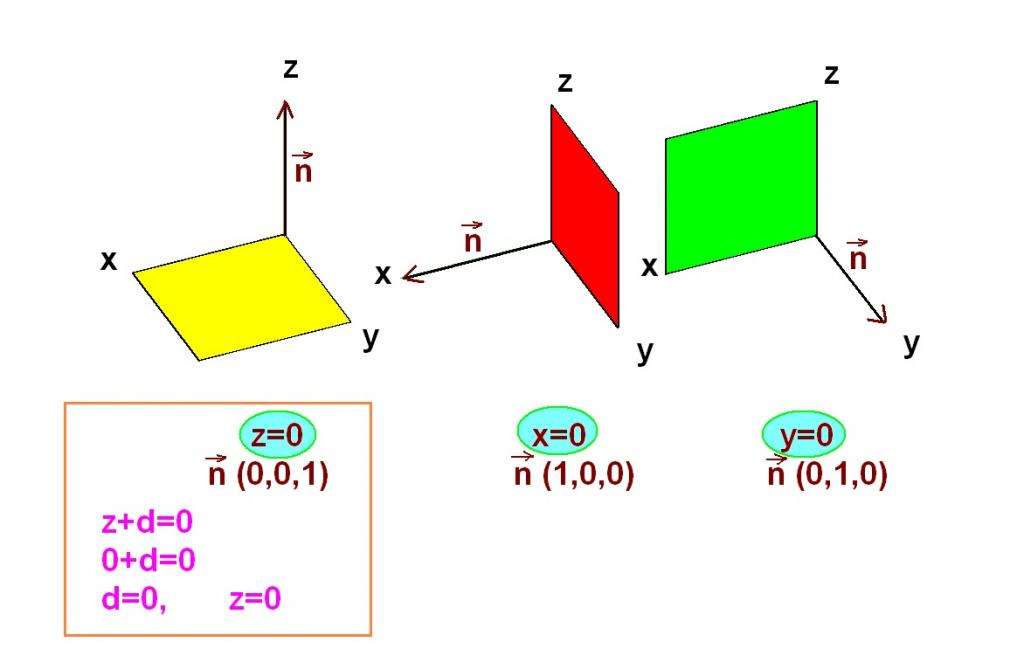
Предположим, что имеется вектор n¯ (A; B; C) и точка P (x0; y0; z0). Какому условию будут удовлетворять все точки Q(x; y; z) плоскости? Это условие заключается в перпендикулярности любого вектора PQ¯ нормали n¯. Для двух перпендикулярных векторов скалярное произведение становится равным нулю (cos(90o)=0), запишем это:

(n¯*PQ¯) = 0 или

A*(x-x0)+B*(y-y0)+C*(z-z0) = 0.

Раскрывая скобки, получаем:

A*x + B*y + C*z + (-A*x0-B*y0-C*z0) = 0 или

A*x + B*y + C*z +D = 0, где D = -A*x0-B*y0-C*z0.

Это уравнение называется общим для плоскости. Мы видим, что коэффициенты, стоящие перед переменными x, y и z, являются координатами перпендикулярного вектора n¯. Он называется направляющим для плоскости.

Векторное параметрическое уравнение плоскости

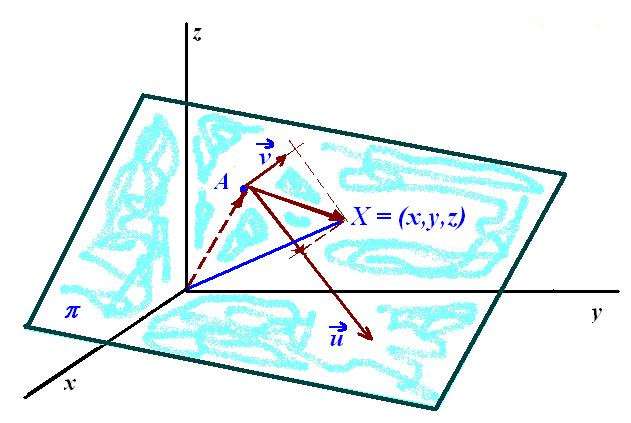
Вторым способом определения плоскости заключается использование двух векторов, лежащих в ней.

Предположим, что имеются векторы u¯(x1; y1; z1) и v¯(x2; y2; z2). Как было сказано, каждый из них в пространстве может быть представлен бесконечным числом одинаковых направленных отрезков, поэтому, для однозначного определения плоскости необходима еще одна точка. Пусть этой точкой будет P(x0; y0; z0). Всякая точка Q(x; y; z) будет лежать в искомой плоскости, если вектор PQ¯ можно представить в виде комбинации u¯ и v¯. То есть имеем:

PQ¯ = α*u¯ + β*v¯.

Где α и β некоторые действительные числа. Из этого равенства следует выражение:

(x; y; z) = (x0; y0; z0) + α*(x1; y1; z1) + β*(x2; y2; z2).

Оно называется параметрическим векторным уравнением плоскости по 2 векторам u¯ и v¯. Подставляя произвольные параметры α и β, можно найти все точки (x; y; z), принадлежащие этой плоскости.

Из этого уравнения легко получить общее выражение для плоскости. Для этого достаточно найти направляющий вектор n¯, который будет перпендикулярен обоим векторам u¯ и v¯, то есть следует применить их векторное произведение.

Задача на определение уравнения плоскости общего вида

Покажем, как пользоваться рассмотренными формулами для решения геометрических проблем. Предположим, что направляющий вектор плоскости равен n¯(5; -3; 1). Следует найти уравнение плоскости, зная, что точка P(2; 0; 0) ей принадлежит.

Общее уравнение записывается в виде:

A*x + B*y + C*z +D = 0.

Поскольку вектор перпендикулярный плоскости известен, то уравнение примет вид:

5*x - 3*y + z +D = 0.

Остается найти свободный член D. Его рассчитываем из знания координат P:

D = -A*x0-B*y0-C*z0 = -5*2 + 3*0 - 1*0 = -10.

Таким образом, искомое уравнение плоскости имеет форму:

5*x - 3*y + z -10 = 0.

Рисунок ниже показывает, что представляет собой полученная плоскость.

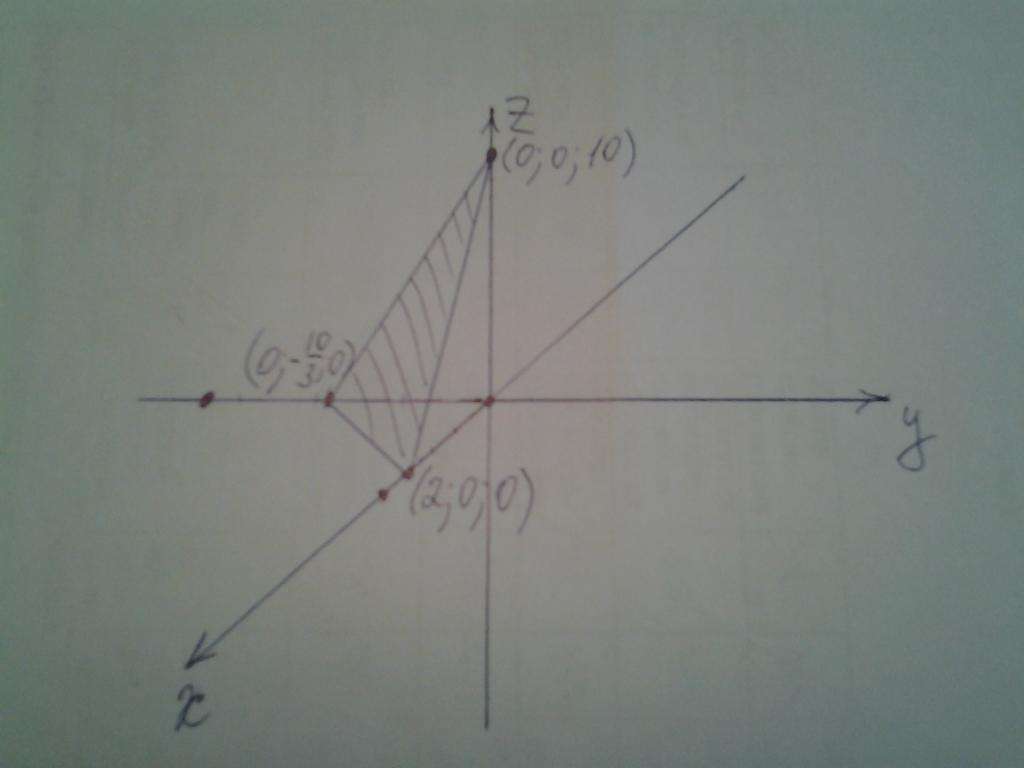
Указанные координаты точек соответствуют пересечениям плоскости с осями x, y и z.

Задача на определение плоскости через два вектора и точку

Теперь предположим, что предыдущая плоскость задана иначе. Известны два вектора u¯(-2; 0; 10) и v¯(-2; -10/3; 0), а также точка P(2;0;0). Как записать уравнение плоскости в векторном параметрическом виде? Воспользовавшись рассмотренной соответствующей формулой, получаем:

(x; y; z) = (2 ; 0 ; 0 ) + α*(-2; 0; 10) + β*(-2; -10/3; 0).

Заметим, что определения этого уравнения плоскости, векторы u¯ и v¯ можно брать абсолютно любые, но с одним условием: они не должны быть параллельными. В противном случае плоскость однозначно определить нельзя, однако, можно найти уравнение для пучка или набора плоскостей.

Источник