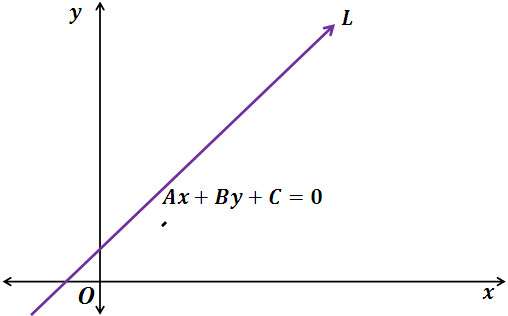Умение находить расстояние между разными геометрическими объектами важно, когда выполняются расчеты площади поверхности фигур и их объемов. В данной статье рассмотрим вопрос о том, как находить от точки до прямой расстояние в пространстве и на плоскости.
Математическое описание прямой
Чтобы понять, как находить расстояние от точки до прямой, следует разобраться с вопросом математического задания этих геометрических объектов.
С точкой все просто, она описывается набором координат, число которых соответствует мерности пространства. Например, на плоскости это две координаты, в трехмерном пространстве - три.
Вам будет интересно:Вычисление угла между прямыми на плоскости и в пространстве: формула
Что касается одномерного объекта - прямой, то для ее описания применяют несколько видов уравнений. Рассмотрим только два из них.
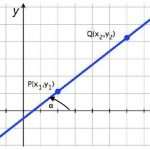
Первый вид называется векторным уравнением. Ниже приведены выражения для прямых в трехмерном и двумерном пространстве:
(x; y; z) = (x0; y0; z0) + α × (a; b; c);
(x; y) = (x0; y0 ) + α × (a; b)
В этих выражениях координаты с нулевыми индексами описывают точку, через которую проходит заданная прямая, набор координат (a; b; c) и (a; b) - это так называемые направляющие вектора для соответствующей прямой, α - это параметр, который может принимать любое действительное значение.
Вам будет интересно:Что такое мрак? Глубинное понимание
Векторное уравнение удобно в том плане, что оно явно содержит вектор направления прямой, координаты которого можно использовать при решении задач параллельности или перпендикулярности разных геометрических объектов, например двух прямых.
Второй вид уравнения, который мы рассмотрим для прямой, называется общим. В пространстве этот вид задается общими уравнениями двух плоскостей. На плоскости же он имеет следующую форму:
A × x + B × y + C = 0
Когда выполняют построение графика, то его часто записывают зависимостью от икса/игрека, то есть:
y = -A / B × x +(-C / B)
Здесь свободный член -C / B соответствует координате пересечения прямой с осью y, а коэффициент -A / B связан с углом наклона прямой к оси x.
Понятие о расстоянии между прямой и точкой
Разобравшись с уравнениями, можно непосредственно переходить к ответу на вопрос о том, как находить от точки до прямой расстояние. В 7 классе школы начинают рассматривать этот вопрос с определения соответствующей величины.
Расстоянием между прямой и точкой называется длина перпендикулярного этой прямой отрезка, который опущен из рассматриваемой точки. Ниже на рисунке изображена прямая r и точка A. Синим цветом показан перпендикулярный прямой r отрезок. Его длина является искомым расстоянием.
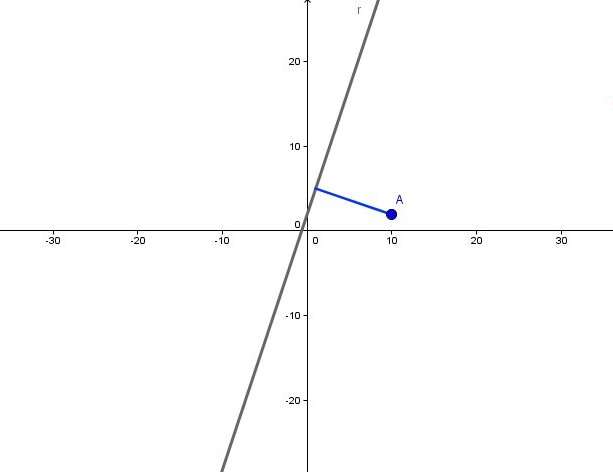
Здесь изображен двумерный случай, тем не менее данное определение расстояния справедливо и для трехмерной задачи.
Необходимые формулы
В зависимости от того, в каком виде записано уравнение прямой и в каком пространстве решается задача, можно привести две основные формулы, дающие ответ на вопрос о том, как найти расстояние между прямой и точкой.
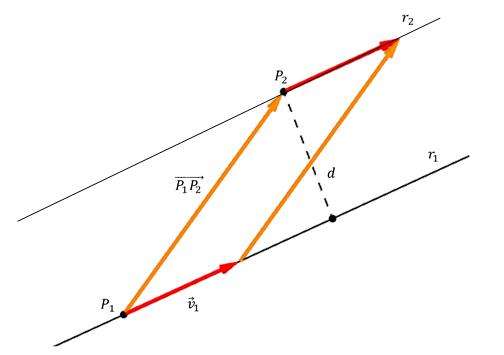
Обозначим известную точку символом P2. Если уравнение прямой задано в векторном виде, то для d расстояния между рассматриваемыми объектами справедлива формула:
d = |[P1P2¯ × v¯]| / |v¯|
То есть для определения d следует вычислить модуль векторного произведения направляющего для прямой вектора v¯ и вектора P1P2¯, начало которого лежит в произвольной точке P1 на прямой, а конец находится в точке P2, затем поделить этот модуль на длину v¯. Эта формула является универсальной для плоского и трехмерного пространства.
Если задача рассматривается на плоскости в системе координат xy и уравнение прямой задано в общем виде, тогда следующая формула найти расстояние от прямой до точки позволяет так:
Прямая: A × x + B × y + C = 0;
Точка: P2(x2; y2; z2);
Расстояние: d = |A × x2 + B × y2 + C| / √(A2 + B2)
Приведенная формула является достаточно простой, однако ее использование ограничено отмеченными выше условиями.
Координаты проекции точки на прямую и расстояние
Ответить на вопрос о том, как находить расстояние от точки до прямой, можно также другим способом, не предполагающим запоминание приведенных формул. Этот способ заключается в определении точки на прямой, которая является проекцией исходной точки.
Предположим, что имеется точка M и прямая r. Проекция на r точки M соответствует некоторой точке M1. Расстояние от M до r равно длине вектора MM1¯.
Как найти координаты M1? Очень просто. Достаточно вспомнить, что вектор прямой v¯ будет перпендикулярен MM1¯, то есть их скалярное произведение должно быть равным нулю. Добавляя к этому условию тот факт, что координаты M1 должны удовлетворять уравнению прямой r, мы получаем систему простых линейных уравнений. В результате ее решения получаются координаты проекции точки M на r.
Описанная в этом пункте методика нахождения расстояния от прямой до точки может использоваться для плоскости и для пространства, однако ее применение предполагает знание векторного уравнения для прямой.
Задача на плоскости
Теперь пришло время показать, как использовать представленный математический аппарат для решения реальных задач. Предположим, что на плоскости задана точка M(-4; 5). Необходимо расстояние найти от точки М до прямой, которая описывается уравнением общего вида:
y = 3 × x + 6
Рекомендуется сразу проверить, принадлежит ли М этой прямой, поскольку в таком случае искомое расстояние будет равно нулю. Подставляем координаты:
3 × (-4) + 6 = -6 ≠ 5
То есть M не лежит на прямой.
Поскольку уравнение прямой задано не в общем виде, приведем его к таковому, чтобы иметь возможность воспользоваться соответствующей формулой, имеем:
y = 3 × x + 6 =>
3 × x - y + 6 = 0
Теперь можно подставлять известные числа в формулу для d:
d = |A × x2 + B × y2 + C| / √(A2+B2) =
= |3 × (-4) -1 × 5+6| / √(32+(-1)2) = 11 / √10 ≈ 3,48
Задача в пространстве
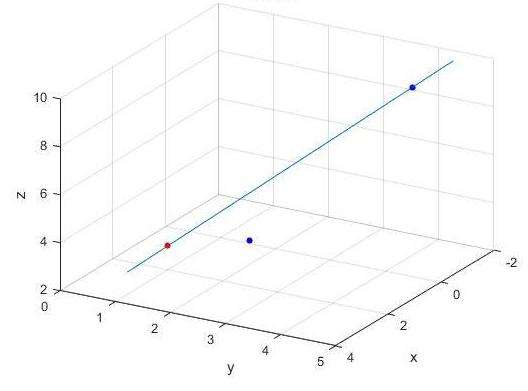
Теперь рассмотрим случай в пространстве. Пусть прямая описывается следующим уравнением:
(x; y; z) = (1; -1 ; 0 ) + α × (3; -2; 1)
Чему равно расстояние от нее до точки M(0; 2; -3)?
Так же, как и в предыдущем случае, проверим принадлежность M заданной прямой. Для этого подставим координаты в уравнение и перепишем его в явном виде:
x = 0 = 1 + 3 × α => α = -1/3;
y = 2 = -1 -2 × α => α = -3/2;
z = -3 = α
Поскольку получены разные параметры α, то M не лежит на этой прямой. Рассчитаем теперь расстояние от нее до прямой.
Чтобы воспользоваться формулой для d, возьмем произвольную точку на прямой, например P(1; -1; 0), тогда:
PM¯(-1; 3; -3)
Вычислим векторное произведение между PM¯ и направляющим вектором прямой v¯. Получаем:
[PM¯*v¯] = [(-1; 3; -3) * (3; -2; 1)] = (-3; -8; -7)
Теперь подставляем модули найденного вектора и вектора v¯ в формулу для d, получаем:
d = √(9 + 64 + 49) / √(9 + 4 + 1) ≈ 2,95
Этот ответ можно было получить, воспользовавшись описанной выше методикой, предполагающей решение системы линейных уравнений. В этой и предыдущей задачах вычисленные значения расстояния от прямой до точки представлены в единицах соответствующей системы координат.
