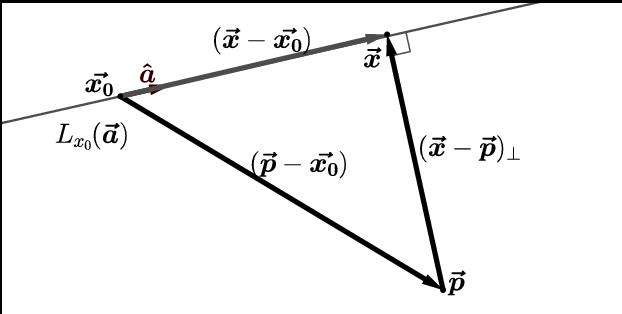
Знание расстояния от точки до плоскости или до прямой позволяет вычислить объем и площадь поверхности фигур в пространстве. Расчет этого расстояния в геометрии осуществляется с использованием соответствующих уравнений для указанных геометрических объектов. В статье покажем, с помощью каких формул можно его определить.
Уравнения прямой и плоскости
Перед тем как приводить формулы для определения расстояния от точки до плоскости и до прямой, покажем, какими уравнениями описываются эти объекты.
 Вам будет интересно:Как найти проекцию точки на плоскость: методика определения и пример решения задачи
Вам будет интересно:Как найти проекцию точки на плоскость: методика определения и пример решения задачи
Для определения точки используется набор координат в данной системе координатных осей. Здесь будем рассматривать только декартову прямоугольную систему, в которой оси имеют одинаковые единичные векторы и являются взаимно перпендикулярными. На плоскости произвольная точка описывается двумя координатами, в пространстве - тремя.
Для определения прямой используют разные типы уравнений. В соответствии с темой статьи, приведем лишь два из них, которые применяются в двумерном пространстве для задавания прямых.
Векторное уравнение. Оно имеет следующую форму записи:
(x; y) = (x0; y0 ) + λ*(a; b).
Первый член здесь представляет координаты известной точки, лежащей на прямой. Второй член - это координаты направляющего вектора, умноженные на произвольное число λ.
Уравнение общего вида. Его форма записи такая:
A*x + B*y + C = 0;
где A, B, C - некоторые коэффициенты.
Общее уравнение чаще используется для определения прямых на плоскости, однако для нахождения расстояния от точки до прямой на плоскости удобнее работать с векторным выражением.
Плоскость в трехмерном пространстве тоже можно записать несколькими математическими способами. Тем не менее чаще всего в задачах встречается уравнение общего вида, которое записывается так:
A*x + B*y + C*z + D = 0.
Преимуществом этой формы записи по отношению к остальным является то, что она в явном виде содержит координаты вектора, перпендикулярного плоскости. Этот вектор называется направляющим для нее, он совпадает с направлением нормали, а его координаты равны (A; B; C).
Заметим, что приведенное выражение совпадает с формой записи уравнения общего вида для прямой в двумерном пространстве, поэтому при решении задач стоит быть внимательным и не путать эти геометрические объекты.
Дистанция между точкой и прямой
Покажем, как можно вычислить расстояние между прямой и точкой в двумерном пространстве.
Пусть имеется некоторая точка Q(x1; y1) и прямая, заданная выражением:
(x; y) = (x0; y0 ) + λ*(a; b).
Под дистанцией между прямой и точкой понимают длину перпендикулярного этой прямой отрезка, опущенного на нее из точки Q.
Перед тем как вычислять это расстояние, следует подставить координаты Q в это равенство. Если они ему будут удовлетворять, значит Q принадлежит данной прямой, и соответствующее расстояние равно нулю. Если же координаты точки не приводят к соблюдению равенства, тогда расстояние между геометрическими объектами отлично от нуля. Его можно рассчитать по формуле:
d = |[PQ¯*u¯]|/|u¯|.
Здесь P - произвольная точка прямой, которая является началом вектора PQ¯. Вектор u¯ - это направляющий отрезок для прямой, то есть его координаты равны (a; b).
Использование этой формулы предполагает умение вычислять векторное произведение, стоящее в числителе.
Задача с точкой и прямой
Допустим, необходимо найти дистанцию между Q(-3; 1) и прямой, удовлетворяющей уравнению:
y = 5*x -2.
Подставив координаты Q в выражение, можно убедиться, что Q на прямой не лежит. Применить приведенную в пункте выше формулу для d можно, если представить данное уравнение в векторном виде. Сделаем это следующим образом:
(x; y) = (x; 5*x -2) =>
(x; y) = (x; 5*x) + (0; -2) =>
(x; y) = x*(1; 5) + (0; -2) =>
(x; y) = (0; -2) + λ*(1; 5).
Теперь возьмем любую точку на этой прямой, например (0; -2), и построим вектор с началом в ней и концом в Q:
(-3; 1) - (0; -2) = (-3; 3).
Теперь применяем формулу для определения расстояния, получаем:
d = |[(-3; 3)*(1; 5)]|/|(1; 5)| = 18/√26 ≈ 3,53.
Расстояние от точки до плоскости
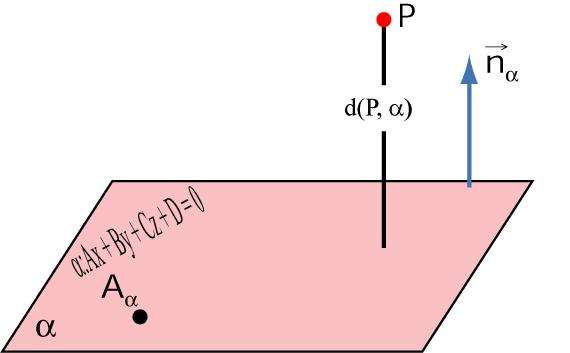
Как и в случае с прямой, под дистанцией между плоскостью и точкой в пространстве понимают длину отрезка, который из данной точки перпендикулярно опущен на плоскость и пересекает ее.
В пространстве точка задается тремя координатами. Если они равны (x1; y1; z1), тогда расстояние между плоскостью и этой точкой можно вычислить по формуле:
d = |A*x1 + B*y1 + C*z1 + D|/√(A2+B2+C2).
Отметим, что использование формулы позволяет найти только расстояние от плоскости до прямой. Чтобы найти координаты точки, в которой перпендикулярный отрезок пересекает плоскость, необходимо составить уравнение прямой, которой этот отрезок принадлежит, а затем найти общую точку для этой прямой и заданной плоскости.
Задача с плоскостью и точкой
Найдите расстояние от точки до плоскости, если известно, что точка имеет координаты (3; -1; 2), а плоскость задана выражением:
-y + 3*z = 0.
Чтобы воспользоваться соответствующей формулой, выпишем сначала коэффициенты для заданной плоскости. Поскольку переменная x и свободный член отсутствуют, то коэффициенты A и D равны нулю. Имеем:
A = 0; B = -1; C = 3; D = 0.
Легко показать, что эта плоскость проходит через начало координат, и ось x ей принадлежит.
Подставляем координаты точки и коэффициенты плоскости в формулу для дистанции d, получаем:
d = |0*3 + (-1)*(-1) + 2*3 + 0|/√(1 +9 ) = 7/√10 ≈ 2,21.
Заметим, что если изменить координату x точки, то расстояние d не изменится. Этот факт означает, что совокупность точек (x; -1; 2) образует прямую, параллельную заданной плоскости.