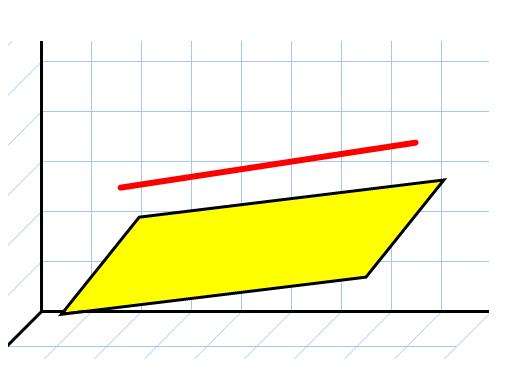
Базовыми геометрическими элементами являются точка, прямая и плоскость. Они называются так потому, что из них можно построить многие объекты, например, такие как пирамида или призма. Чтобы понять свойства этих фигур, важно знать взаимное расположение в пространстве прямых и плоскостей. Рассмотрим подробнее этот вопрос в статье.
Определение и описание точки, прямой и плоскости
 Вам будет интересно:Пополняем словарный запас: неказистый — это...
Вам будет интересно:Пополняем словарный запас: неказистый — это...
Точкой в геометрии называется 0-мерный объект, единственной характеристикой которого являются его координаты. Последние представляют собой набор чисел, привязанный к конкретной системе. Например, на плоскости он состоит из двух элементов, в трехмерном пространстве - из трех.
Прямая - это одномерный объект, который обладает некоторым направлением. Если соединить ее любые две точки, то получится вектор, который ее характеризует. Для описания прямых используют несколько типов уравнений, которые с помощью несложных математических операций могут быть переведены друг в друга. Здесь приведем лишь векторное, которое часто применяется для анализа взаимного расположения в пространстве прямых. Оно для трехмерного случая принимает форму:
 Вам будет интересно:Обзор основных вузов Сургута
Вам будет интересно:Обзор основных вузов Сургута
(x; y; z) = (x0; y0; z0) + α*(a; b; c)
Элементы с нулевыми индексами соответствуют некоторой точке, которая является частью прямой. Координаты, которые умножаются на параметр α (альфа) описывают ее направляющий вектор, вдоль которого она проходит. Подставляя произвольные числа α можно найти все точки, которые образуют прямую в пространстве.
Очевидно, что для векторного уравнения в двумерном пространстве необходимо использовать лишь две координаты для точек и векторов.
Плоскость является совокупностью точек. Образованные на них вектора перпендикулярны некоторому направлению, задаваемому нормальным к плоскости вектором. Все это можно описать несколькими способами. Тем не менее, для решения задач на определение взаимного расположения плоскости и прямой удобно пользоваться уравнением общего вида. Оно записано ниже:
A*x + B*y + C*z + D = 0
Удобство этой формы записи заключается в том, что коэффициенты A, B, C являются координатами перпендикулярного вектора n¯ к плоскости.
При решении задач важно учитывать, в каком пространстве решается проблема. Так, приведенный вид уравнения плоскости в двумерном случае без координаты z будет соответствовать уравнению прямой.
Расположение точки и прямой
 Вам будет интересно:«Соразмерно» — это и «в рамках», и «гармонично»
Вам будет интересно:«Соразмерно» — это и «в рамках», и «гармонично»
Взаимное расположение этих объектов не зависит от того, рассматриваются они на плоскости или в пространстве. Критерии определения постоянно одни и те же.
Относительно прямой точка может находиться лишь в двух возможных положениях:
- лежать на ней;
- либо не принадлежать ей.
Определить вариант расположения в конкретной задаче достаточно легко. Для этого следует подставить координаты искомого объекта в уравнение, задающее прямую. Если равенство будет выполняться, значит, точка принадлежит прямой. В противном случае она не является ее частью.
Две прямые на плоскости
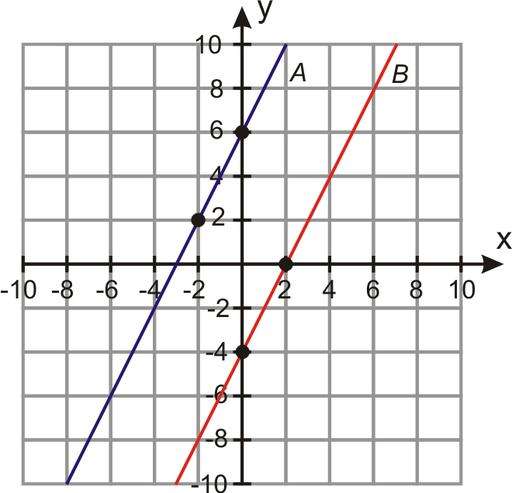
Какое может быть взаимное расположение двух прямых на плоскости? Существует три разных варианта:
Чтобы понять, каково взаимное расположение прямых в конкретном случае, необходимо провести некоторый математический анализ. Ниже описываются основные идеи, которые следует использовать при его осуществлении.
Если направляющие векторы прямых параллельны друг другу, значит и прямые, как минимум, будут параллельными. Параллельность векторов доказывается, если один из них можно представить в виде другого, умноженного на действительное число.
Если направляющие вектора параллельны, и хотя бы одна точка одной прямой соответствует и другой прямой, тогда речь идет о полностью совпадающих прямых.
Если направляющие вектора не являются параллельными, то прямые пересекаются в одной точке. Найти ее координаты можно с помощью решения системы уравнений (эти координаты должны соответствовать обоим уравнениям прямых).
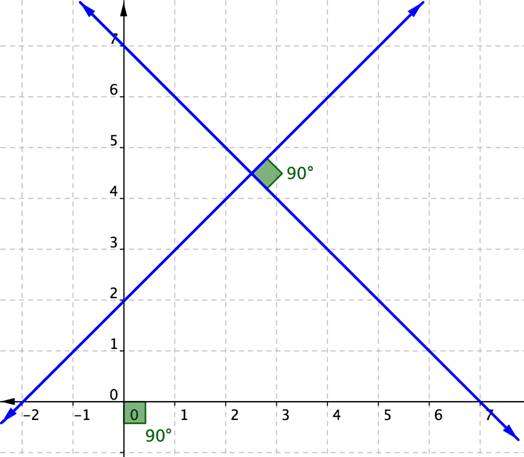
Частным случаем пересечения прямых является угол пересечения, равный 90o. В таком случае говорят о перпендикулярности между рассматриваемыми объектами. Если две прямые перпендикулярны, то скалярное произведение их векторов направляющих будет равно нулю.
Прямая и окружность на плоскости
Поскольку данный объект часто появляется в геометрических задачах, то полезно также рассмотреть вопрос взаимного расположения окружности и прямой. Возможны такие варианты:
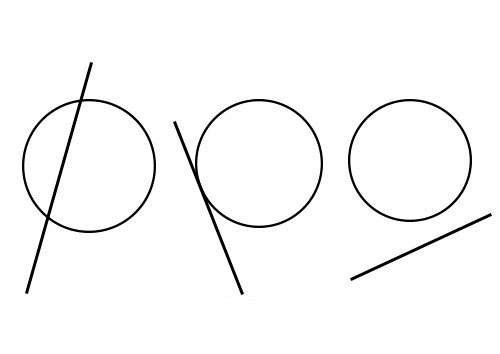
Определить вариант расположения этих объектов для конкретной задачи можно с использованием соответствующих уравнений. Для окружности с центром в (x0; y0) и радиусом R оно имеет вид:
R2 = (x-x0)2 + (y-y0)2
Определение варианта расположения сводится к решению квадратного уравнения.
Две прямые в пространстве
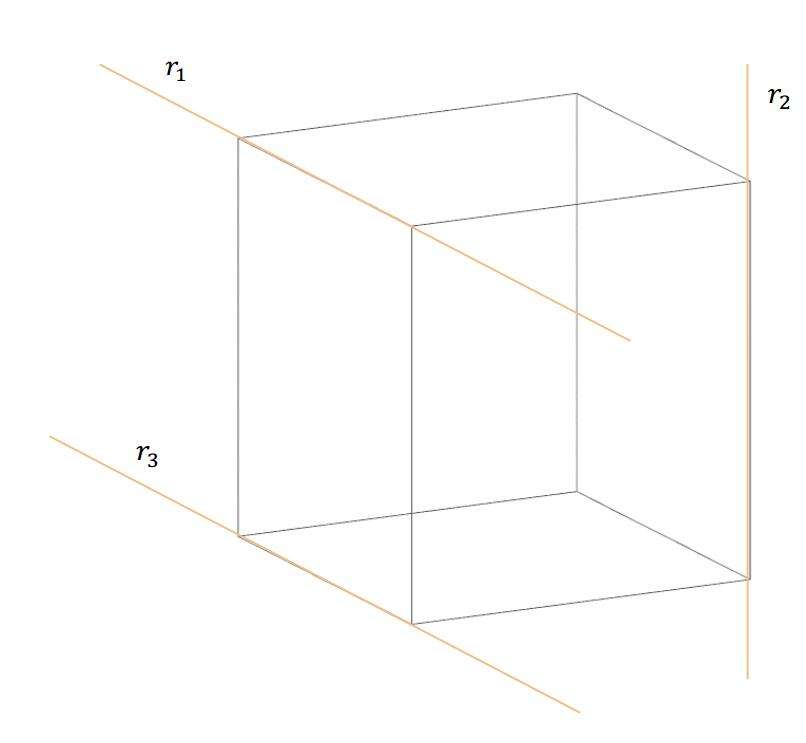
Часто возникает вопрос о том, каково взаимное расположение прямых в пространстве трехмерном. Возможны те же самые варианты, что описаны в предыдущем пункте, однако, к ним добавляется еще один. Скрещивающиеся прямые и не пересекаются, и не являются параллельными. Подробнее - ниже.
Определить, являются ли рассматриваемые одномерные объекты скрещивающимися, также не представляет особого труда. В первую очередь, необходимо выяснить, что их направляющие векторы не параллельные. После этого проще всего рассчитать расстояние между прямыми. Если оно равно нулю, значит, они пересекаются, если отличается (больше или меньше) - тогда они скрещивающиеся.
Расчет расстояния производится по формуле:
d = |[M1M2¯*v¯]|/|v¯|,
где:
- v¯ - направляющий вектор первой прямой;
- M1M2¯ - вектор, построенный на произвольных точках M1 и M2 первой и второй прямой соответственно.
Формулу можно непосредственно применить, если даны векторные уравнения прямых.
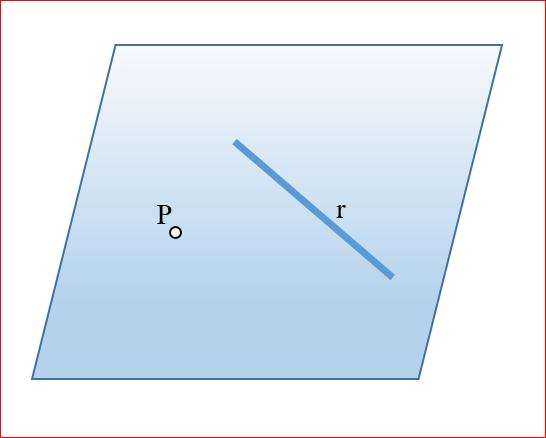
Плоскость и прямая
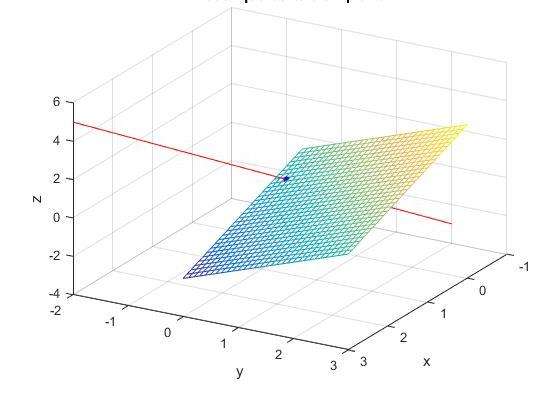
В данном случае речь идет о трехмерном пространстве. Взаимное расположение плоскости и прямой возможно следующее:
Определить параллельность этих геометрических объектов достаточно просто. Для этого нужно рассчитать скалярное произведение нормального вектора плоскости и направляющего вектора прямой. Равенство нулю этого произведения является достаточным условием параллельности. Если к тому же хотя бы одна точка принадлежит плоскости, значит, вся прямая лежит в ней.
Если скалярное произведение нулю не равно, тогда вывод следующий. Прямая и плоскость пересекаются в одной точке. Частным случаем является пересечение под прямым углом. Если направляющий вектор прямой можно представить в виде произведения на число вектора нормали к плоскости, значит, прямая и плоскость перпендикулярны.
Задача с двумя прямыми на плоскости
Ниже даны два уравнения в общем виде для прямых в двумерном пространстве:
2*x - y = 7;
-3*x + 2*y = 0.
Необходимо определить взаимное расположение прямых.
Поскольку имеет место случай на плоскости, то нет необходимости приводить эти уравнения к векторному виду. Решить задачу можно проще, если найти корни системы из этих них. Имеем:
2*x - y = 7 => y = 2*x - 7;
-3*x + 2*y = 0 => -3*x + 2*(2*x - 7) = 0 =>
x = 14; y = 21.
Поскольку система имеет единственное решение, то оно соответствует пересечению рассматриваемых прямых в точке (14; 21).
Задача с двумя прямыми в пространстве
Даны две прямые, которые описываются уравнениями:
r1: (x; y; z) = (1 ; -2; 0 ) + α*(2; -1; 1);
r2: (x; y; z) = (2; 2; 1) + β*(0; 3; -1).
Каково взаимное расположение прямых в пространстве?
Можно заметить, что направляющие вектора параллельными не являются (никакое значение параметра β не способно дать направляющий вектор r1). То есть прямые либо пересекаются, либо являются скрещивающимися.
Вычислим расстояние между ними. Для этого на r1 возьмем точку M1(1; -2; 0), а на r2 - точку M2(2; 2; 1). Тогда вектор, соединяющий их, равен:
M1M2¯ = (1; 4; 1).
Его векторное произведение с направляющим вектором для r1 равно:
[(1; 4; 1)*(2; -1; 1)] = (5; 1; -9).
Поскольку длина этого вектора отлична от нуля, значит, расстояние между прямыми будет больше нуля. Последний факт говорит, что они не имеют общих точек и являются скрещивающимися.