Многие геометрические фигуры образованы пересекающимися под прямым углом прямыми. Например, это квадрат, прямоугольник, прямоугольный треугольник или прямая четырехугольная призма. В данной статье рассмотрим вопрос перпендикулярности двух прямых и условия, которые должны выполняться, чтобы прямая была перпендикулярна плоскости.
Какие уравнения важно знать?
Условия перпендикулярности двух прямых и прямой и плоскости не сложно получить, если известны соответствующие уравнения для названных геометрических объектов.
 Вам будет интересно:Система Тейлора, ее проблемы и достоинства
Вам будет интересно:Система Тейлора, ее проблемы и достоинства
Уравнение любой прямой как на плоскости, так и в пространстве может быть записано в универсальном векторном виде. Для трехмерного случая оно выглядит следующим образом:
(x; y; z) = (x0; y0; z0) + λ*(a; b; c)
Здесь переменные x, z и y являются координатами в выбранной системе, λ - любое действительное число, а тройка чисел (a; b; c) задают вектор в пространстве, который называется направляющим (вдоль него направлена прямая, проходящая через точку с координатами (x0; y0; z0)). Это уравнение может быть преобразовано в общий вид, в каноническое и параметрическое.
Плоскость удобнее всего представлять в общем виде, что соответствует уравнению:
A*x + B*y + C*z + D = 0
Большие латинские буквы представляют собой коэффициенты. Это выражение также может быть представлено в векторном, параметрическом видах и в форме уравнения в отрезках. Удобство приведенной формы записи заключается в том, что первые три коэффициента соответствуют координатам вектора, который перпендикулярен этой плоскости, то есть:
n¯(A; B; C) - направляющий вектор плоскости
Перпендикулярность двух прямых
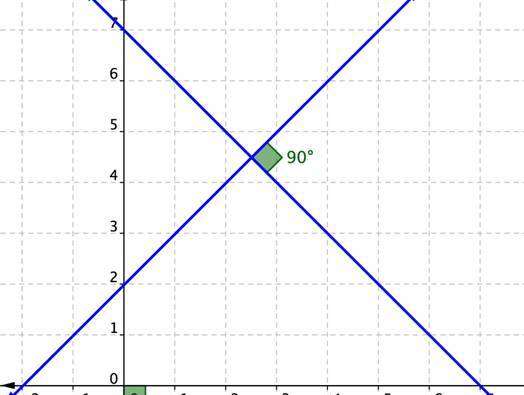
Условие перпендикулярности прямых не сложно понять, для этого достаточно установить, являются ли перпендикулярными их направляющие вектора. Последнее можно выяснить, вычислив скалярное произведение. Предположим, что v¯ и u¯ - вектора направляющие для двух прямых. Если последние являются перпендикулярными, тогда:
(v¯*u¯) = 0
Это условие перпендикулярности двух прямых является обязательным. Тем не менее, оно будет достаточным только для случая двумерного пространства. В трехмерном же пространстве, помимо этого выражения, также следует вычислить расстояние между прямыми. Если равенство выше выполняется, и указанное расстояние равно нулю, тогда прямые будут пересекаться под углом 90o, то есть будут перпендикулярными.
Для расчета дистанции d между прямыми в пространстве пользуются выражением:
d = |[M1M2¯*u¯]|/|u¯|
Здесь M1M2¯ - вектор, построенный на двух точках, каждая из которых принадлежит соответствующей прямой (M1 лежит на первой прямой, M2 - на второй).
Плоскость и прямая
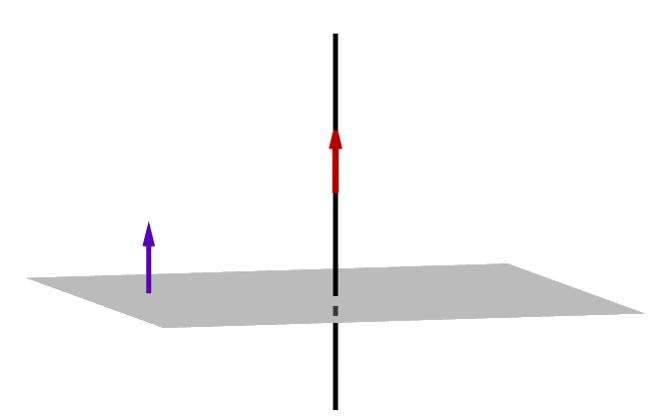
Перпендикулярности условие для этих объектов имеет следующий вид:
u¯ = k*n¯
Иными словами, прямая будет пересекать плоскость под углом 90o только тогда, когда ее направляющий вектор будет параллелен нормали к плоскости. Факт параллельности означает, что вектор прямой u¯ можно получить, умножив нормальный к плоскости вектор n¯ на некоторое конкретное число k.
Существуют также другие способы узнать, являются ли параллельными вектора u¯ и n¯. Например, в случае их параллельности угол между ними должен быть равен нулю, то есть косинус угла, рассчитанного через скалярное произведение, будет равен 1. В свою очередь векторное произведение параллельных векторов равно нулю.
Заметим, если плоскость и прямая заданы не в общем и векторном виде, соответственно, тогда следует привести их к этим видам, а затем пользоваться приведенными формулами условий перпендикулярности.
