Одной из самых простых объемных фигур является треугольная пирамида, поскольку она состоит из наименьшего числа граней, из которого можно образовать фигуру в пространстве. В данной статье рассмотрим формулы, с помощью которых можно найти объем треугольной правильной пирамиды.
Треугольная пирамида
Согласно общему определению пирамида представляет собой многоугольник, все вершины которого соединены с одной точкой, не расположенной в плоскости этого многоугольника. Если последний представляет собой треугольник, то вся фигура называется треугольной пирамидой.
 Вам будет интересно:Ударение в "балует" и "баловать" не падает на слог "бал"
Вам будет интересно:Ударение в "балует" и "баловать" не падает на слог "бал"
Рассматриваемая пирамида состоит из основания (треугольника) и трех боковых граней (треугольников). Точка, в которой соединены три боковые грани, называется вершиной фигуры. Опущенный на основание перпендикуляр из этой вершины является высотой пирамиды. Если точка пересечения перпендикуляра с основанием совпадает с точкой пересечения медиан треугольника в основании, тогда говорят о правильной пирамиде. В противном случае она будет наклонной.
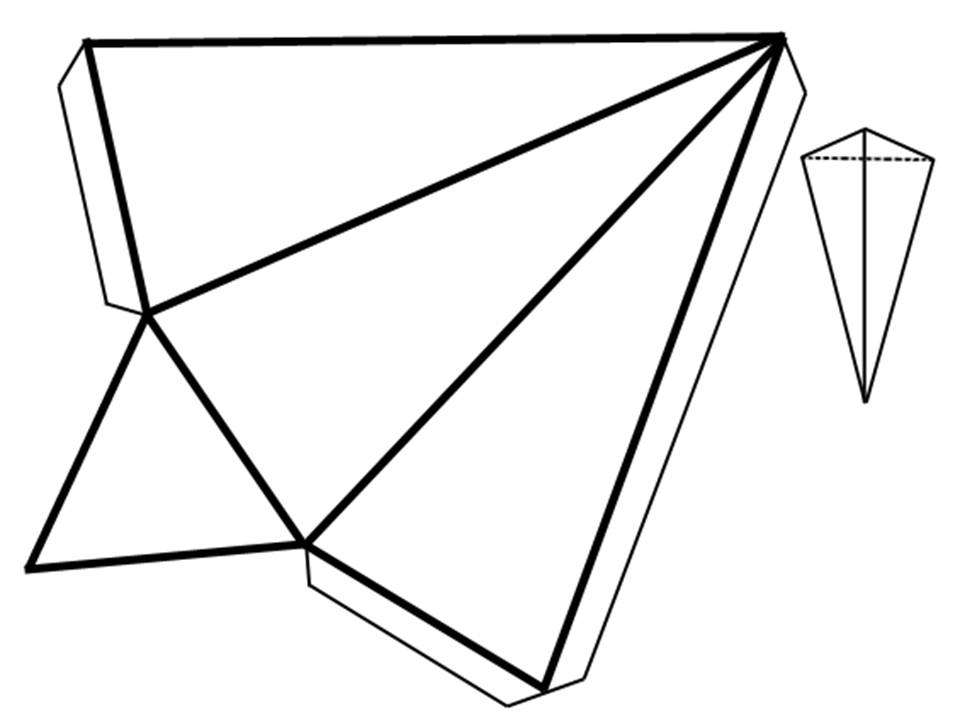
Как было сказано, основание треугольной пирамиды может представлять собой треугольник общего типа. Однако если он является равносторонним, а сама пирамида прямой, тогда говорят о правильной объемной фигуре.
Любая треугольная пирамида имеет 4 грани, 6 ребер и 4 вершины. Если длины всех ребер равны между собой, тогда такая фигура называется тетраэдром.
Объем пирамиды треугольной общего типа
Прежде чем записать формулу объема правильной треугольной пирамиды, приведем выражение этой физической величины для пирамиды общего типа. Это выражение имеет вид:
V = 1/3*So*h.
Здесь So - площадь основания, h - высота фигуры. Это равенство будет справедливым для любого типа основания многоугольника пирамиды, а также для конуса. Если же в основании находится треугольник, имеющий длину стороны a и высоту ho, опущенную на нее, тогда формула для объема запишется так:
V = 1/6*a*ho*h.
Формулы объема правильной треугольной пирамиды
Правильная пирамида треугольная имеет равносторонний треугольник в основании. Известно, что высота этого треугольника связана с длиной его стороны равенством:
ho = √3/2*a.
Подставляя это выражение в формулу для объема треугольной пирамиды, записанную в предыдущем пункте, получаем:
V = 1/6*a*ho*h = √3/12*a2*h.
Объем правильной пирамиды с треугольным основанием является функцией длины стороны основания и высоты фигуры.
Поскольку любой правильный многоугольник можно вписать в окружность, радиус которой однозначно определит длину стороны многоугольника, тогда эту формулу можно записать через соответствующий радиус r:
V = √3/4*h*r2.
Эту формулу легко получить из предыдущей, если учесть, что радиус r описанной окружности через длину стороны a треугольника определяется выражением:
r = a/√3.
Задача на определение объема тетраэдра
Покажем, как использовать приведенные выше формулы при решении конкретных задач геометрии.
Известно, что тетраэдр имеет длину ребра 7 см. Найдите объем правильной треугольной пирамиды-тетраэдра.
Напомним, что тетраэдр является правильной треугольной пирамидой, в которой все основания равны между собой. Чтобы воспользоваться формулой объема правильной пирамиды треугольной, необходимо вычислить две величины:
- длину стороны треугольника;
- высоту фигуры.
Первая величина известна из условия задачи:
a = 7 см.
Чтобы определить высоту, рассмотрим фигуру, изображенную на рисунке.
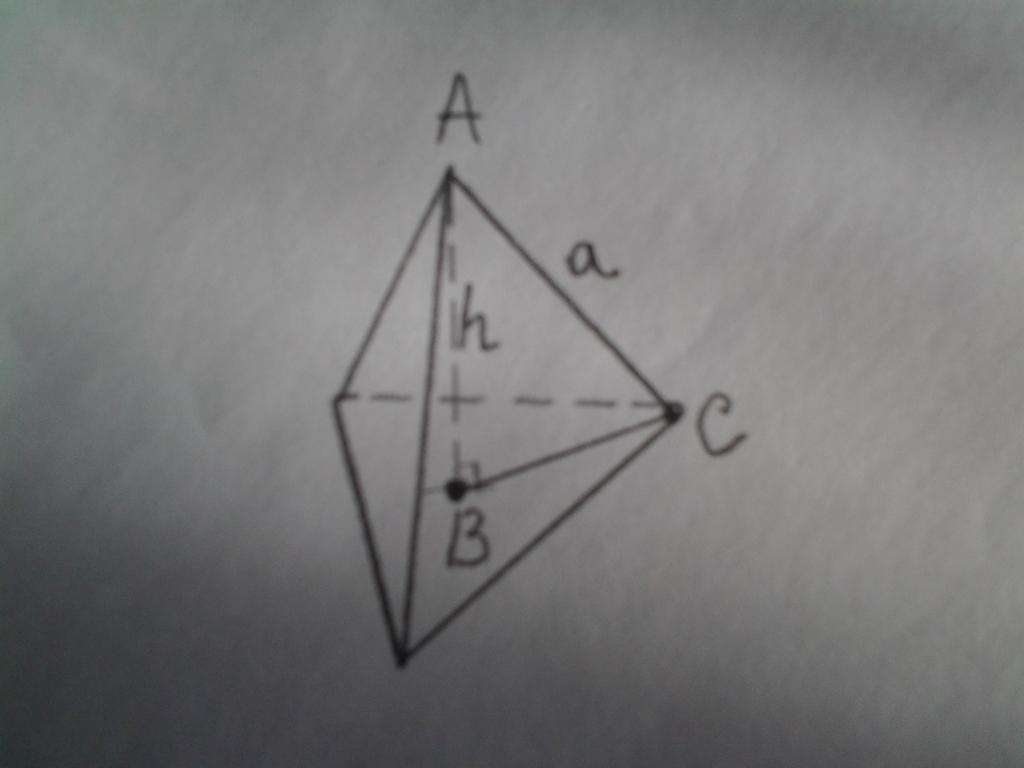
Отмеченный треугольник ABC является прямоугольным, где угол ABC равен 90o. Сторона AC - это гипотенуза, длина которой равна a. Путем несложных геометрических рассуждений можно показать, что сторона BC имеет длину:
BC = a/√3.
Заметим, что длина BC является радиусом описанной вокруг треугольника окружности.
Высоту пирамиды h можно рассчитать, применяя теорему Пифагора. Имеем:
h = AB = √(AC2 - BC2) = √(a2 - a2/3) = a*√(2/3).
Теперь можно h и a подставить в соответствующую формулу для объема:
V = √3/12*a2*a*√(2/3) = √2/12*a3.
Таким образом, мы получили формулу объема тетраэдра. Видно, что объем зависит только от длины ребра. Если в выражение подставить значение из условия задачи, тогда получаем ответ:
V = √2/12*73 ≈ 40,42 см3.
Если сравнить эту величину с объемом куба, имеющим такое же ребро, то получим, что объем тетраэдра в 8,5 раз меньше. Это свидетельствует о том, что тетраэдр является компактной фигурой, которая реализуется в некоторых природных веществах. Например, молекула метана имеет тетраэдрическую форму, а каждый атом углерода в алмазе соединен с четырьмя другими атомами, образующими тетраэдр.
Задача с гомотетичными пирамидами
Решим одну любопытную геометрическую задачу. Предположим, что имеется треугольная правильная пирамида с некоторым объемом V1. Во сколько раз следует уменьшить размеры этой фигуры, чтобы получить гомотетичную ей пирамиду с объемом, в три раза меньшим исходного?
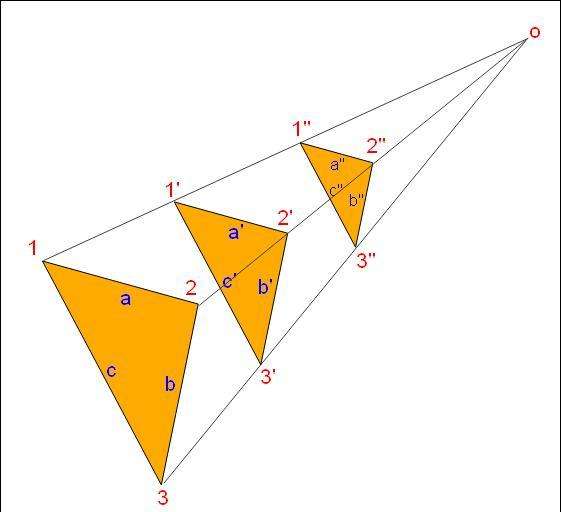
Задачу начнем решать с записи формулы для исходной правильной пирамиды:
V1 = √3/12*a12*h1.
Пусть необходимый по условию задачи объем фигуры получится, если умножить ее параметры на коэффициент k. Имеем:
V2 = √3/12*k2*a12*k*h1 = k3*V1.
Поскольку из условия известно отношение объемов фигур, то получаем значение коэффициента k:
k = ∛(V2/V1) = ∛(1/3) ≈ 0,693.
Отметим, что аналогичное значение коэффициента k мы бы получили для пирамиды произвольного типа, а не только для правильной треугольной.

