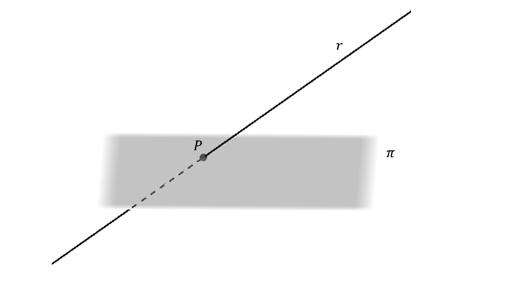
Знание углов между плоскостями и прямыми необходимо при изучении свойств объемных фигур, например пирамид или призм. Вычислить этот угол не сложно. Достаточно знать уравнения прямой и плоскости и соответствующую формулу. Рассмотрим вопрос нахождения отмеченного угла в статье.
Математическое описание прямой и плоскости
Оба геометрических объекта, упомянутых в названии пункта, описываются уравнениями разного типа. Здесь мы не будем приводить все их, а лишь охарактеризуем векторное выражение для прямой и общее уравнение для плоскости, поскольку именно эти типы равенств удобно использовать при расчете угла между прямой и плоскостью.
Вам будет интересно:Что такое гридница в Древней Руси?
Уравнение в векторном виде для прямой в трехмерном пространстве имеет следующую форму записи:
(x; y; z) = (x0; y0; z0) + α * (a; b; c)
Первое слагаемое в скобках - это некоторая известная точка, принадлежащая прямой. Второе слагаемое - координаты вектора, направленного вдоль прямой. Параметр α может принимать любые числовые значения, благодаря чему вычисляются координаты всех точек этой прямой.
Плоскость общим уравнением задается в таком виде:
Вам будет интересно:Кто такой декан? Функции, права, особенности должности
A * x + B * y + C * z + D = 0
Большие латинские буквы - это определенные фиксированные числа. Преимущество этой формы записи по отношению к другим типам выражений для плоскости заключается в том, что из нее удобно находить координаты вектора, перпендикулярного этому двумерному объекту. Эти координаты равны:
n¯(A; B; C)
Записанный вектор называется нормальным или направляющим для плоскости.
Отметим, что знание этого вектора позволяет записать семейство параллельных плоскостей, которые друг от друга отличаются свободным членом D. Чтобы однозначно определить плоскость, помимо n¯, необходимо знать еще одну точку, принадлежащую ей.
Прямая и плоскость в пространстве
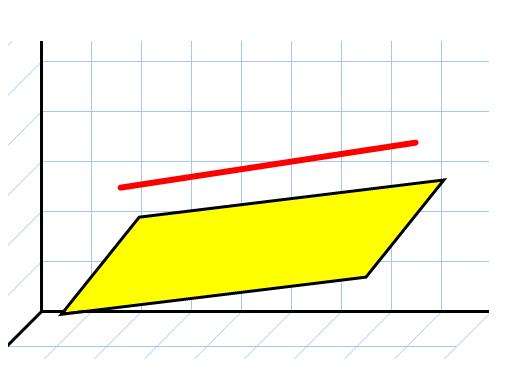
Расчет угла между прямой и плоскостью можно проводить, если понимать, какие варианты в принципе существуют во взаимном расположении этих объектов. Этих вариантом всего три:
- прямая плоскости параллельна, но в ней не лежит;
- все точки прямой также являются точками плоскости;
- прямая с плоскостью пересекаются.
Первые два варианта соответствуют углу 0o между рассматриваемыми геометрическими объектами. В случае же пересечения угол отличен от нуля, но он всегда меньше или равен прямому углу. Если при пересечении плоскости и прямой в одной точке угол равен 90o, то их считают взаимно перпендикулярными.
На рисунке выше прямая и плоскость параллельны друг другу, а на схеме ниже они пересекаются.
Формула угла между прямой и плоскостью
Получим формулу для рассматриваемой величины в общем виде. Для этого запишем еще раз представленные уравнения прямой и плоскости:
(x; y; z) = (x0; y0; z0) + λ * (a; b; c);
A * x + B * y + C * z + D = 0
Предположим для простоты вывода, что прямая плоскость пересекает. Согласно определению, углом между ними называется угол между этой прямой и ее проекцией на плоскость. Для получения проекции достаточно опустить перпендикуляр из произвольной точки прямой на плоскость, а затем через полученную точку на плоскости и точку пересечения провести прямую. Соответствующий рисунок изображен ниже, где символом α отмечен искомый угол.
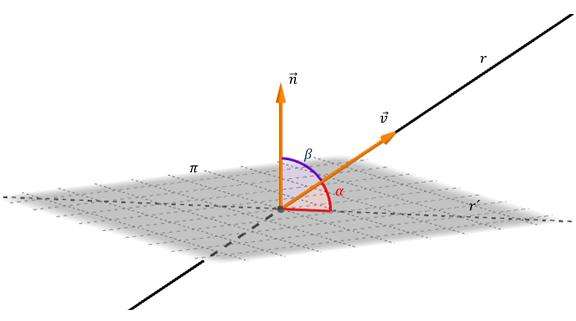
На рисунке также изображен направляющий вектор прямой v¯ и нормаль n¯, отмечен угол β между ними. Из рисунка видно, что эти углы связаны друг с другом выражением:
β + α = 90o
Как найти β, сможет ответить любой школьник, который знаком со свойствами скалярного произведения. Для этого достаточно вычислить его и поделить на произведение модулей соответствующих векторов, то есть:
cos(β) = |(n¯ * v¯)| / (|n¯| * |v¯|)
Обращаем внимание, что в числителе стоит модуль произведения. Это позволяет находить только прямые углы пересечения.
Из тригонометрических формул известно следующее равенство:
cos(β) = cos(90o - α) = sin(α)
Тогда искомый угол может быть вычислен по формуле:
α = arcsin(|(n¯ * v¯)| / (|n¯| * |v¯|)
Если подставить координаты векторов для записанной выше прямой и плоскости, то получим конечную формулу:
α = arcsin(|(A * a + B * b + C * c)| / (√(A2 + B2 + C2) * √(a2 + b2 + c2))
Покажем, как ее использовать при решении задач.
Плоскость и прямая и значение угла их пересечения
Необходимо найти угол между прямой и плоскостью, заданных выражениями:
(x; y; z) = (1; 1; 0) + λ * (2; -1; 3);
x + y - 2z + 1 = 0
Приведенной формулой для α удобно пользоваться, если предварительно вычислить модули векторов и их скалярное произведение. Сделаем это:
n¯(1; 1; -2);
v¯(2; -1; 3);
(n¯ * v¯) = ((1; 1; -2) * (2; -1; 3)) = -5;
|n¯| = √(1 + 1 + 4) = √6;
|v¯| = √(4 + 1 + 9) = √14
Теперь найденные значения можно подставить в формулу для α:
α = arcsin(|-5| / (√6 * √14)) = 33,06o
Таким образом, мы показали, что плоскость и прямая действительно пересекаются, и угол между ними приблизительно равен 33o.
Пересечение прямой координатных плоскостей
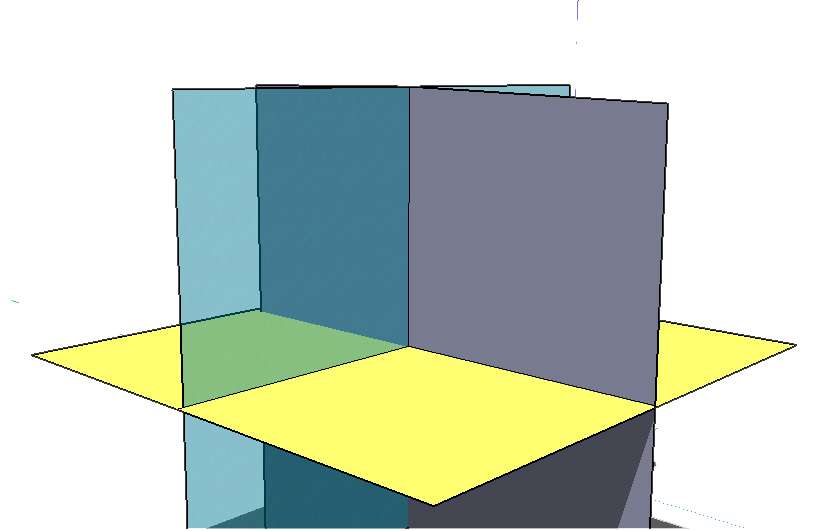
Теперь решим такую задачу. Дана прямая, которая задается следующим образом:
(x; y; z) = (1 ; 0 ; 0 ) + λ * (2; 0; -1)
Необходимо найти углы ее пересечения с тремя координатными плоскостями.
Для начала следует математически записать выражения для указанных плоскостей. Они имеют вид:
x = 0 (плоскость yz);
y = 0 (плоскость xz);
z = 0 (плоскость xy)
Для каждой из них запишем координаты нормального вектора:
n¯(1; 0; 0) для x = 0;
n¯(0; 1; 0) для y = 0;
n¯(0; 0; 1) для z = 0
Видно, что длины всех нормальных векторов равны единице. Находим скалярные произведения для каждого из них с направляющим вектором прямой:
для x = 0: ((2; 0; -1) * (1; 0; 0)) = 2;
для y = 0: ((2; 0; -1) * (0; 1; 0)) = 0;
для z = 0: ((2; 0; -1) * (0; 0; 1)) = -1
Модуль направляющего для прямой вектора равен:
|(2; 0; -1)| = √5
Подставляем рассчитанные значения в формулу, получаем углы пересечения:
с x = 0: α = arcsin(|2| / √5) ≈ 63,4o;
с y = 0: α = arcsin(|0| / √5) =0o;
с z = 0: α = arcsin(|-1| / √5) ≈ 26,6o
Таким образом, заданная прямая пересекает только плоскости yz и xy, а к плоскости xz она является параллельной.
