С разделением математики на алгебру и геометрию учебный материал становится сложнее. Появляются новые фигуры и их частные случаи. Для того чтобы хорошо разобраться в материале, необходимо изучить понятия, свойства объектов и сопутствующие теоремы.
Общие понятия
Под четырехугольником подразумевается геометрическая фигура. Состоит она из 4-х точек. Причем 3 из них не располагаются на одной прямой. Имеются отрезки, последовательно соединяющие указанные точки.
Все четырехугольники, изучаемые в школьном курсе геометрии, показаны в следующей схеме. Вывод: любой объект из представленного рисунка обладает свойствами предыдущей фигуры.
 Вам будет интересно:Гимназия № 1554: описание, адрес
Вам будет интересно:Гимназия № 1554: описание, адрес
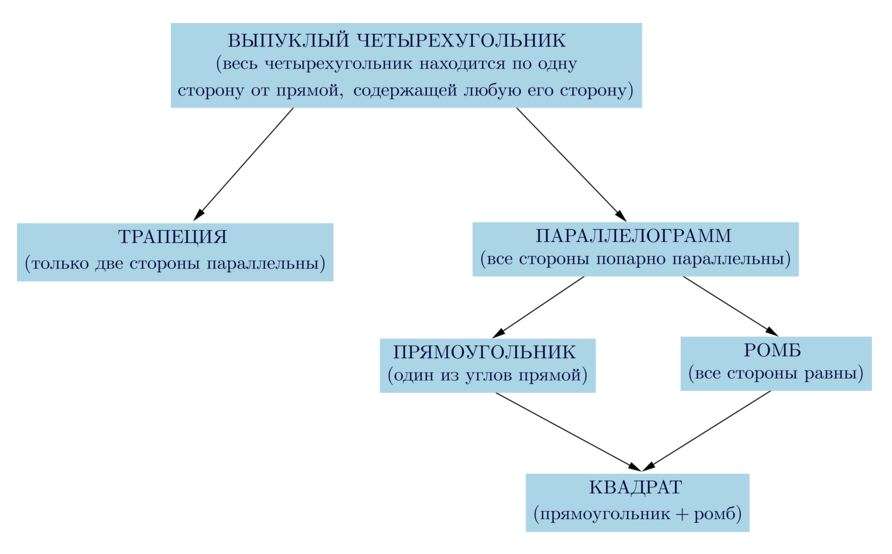
Четырехугольник может быть следующих видов:
- Параллелограмм. Параллельность его противоположных сторон доказывается соответствующими теоремами.
- Трапеция. Четырехугольник, у которого основания параллельны. Другие две стороны – нет.
- Прямоугольник. Фигура, у которой все 4 угла = 90º.
- Ромб. Фигура, у которой все стороны равны.
- Квадрат. Совмещает в себя свойства последних двух фигур. У него все стороны равны и все углы прямые.
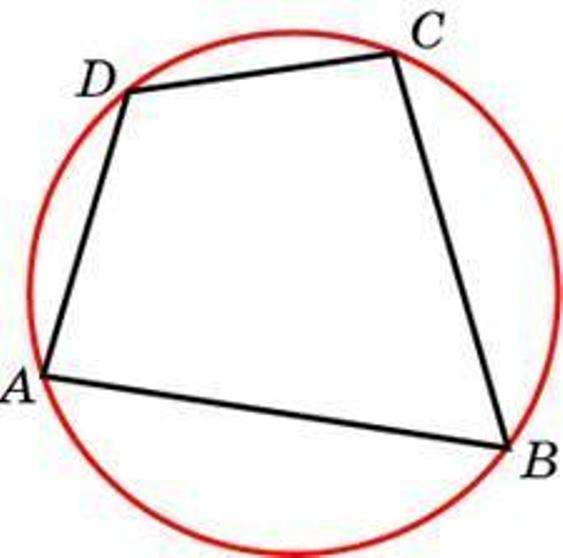
Основное определение данной темы – вписанный четырехугольник в окружность. Оно заключается в следующем. Это фигура, вокруг которой описана окружность. Она должна проходить через все вершины. Внутренние углы четырехугольника, вписанного в окружность, в сумме дают 360º.
Не каждый четырехугольник может быть вписан. Связано это с тем, что серединные перпендикуляры 4-х сторон могут не пересечься в одной точке. Это сделает невозможным нахождение центра окружности, описанной около 4-угольника.
Частные случаи
Из всякого правила есть исключения. Так, в данной теме также имеются частные случаи:
- Параллелограмм, как таковой, не может быть вписан в окружность. Только его частный случай. Это прямоугольник.
- Если все вершины ромба находятся на описывающей линии, то он является квадратом.
- Все вершины трапеции находятся на границе окружности. В таком случае говорят о равнобедренной фигуре.
Свойства вписанного четырехугольника в окружность
Перед решением простых и сложных задач по заданной теме необходимо удостовериться в своих знаниях. Без изучения учебного материала невозможно решить ни один пример.
Теорема 1
Сумма противоположных углов, четырехугольника вписанного в окружность, равна 180º.
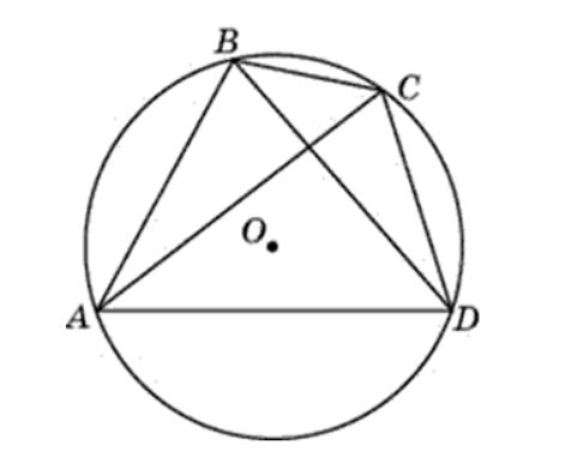
Доказательство
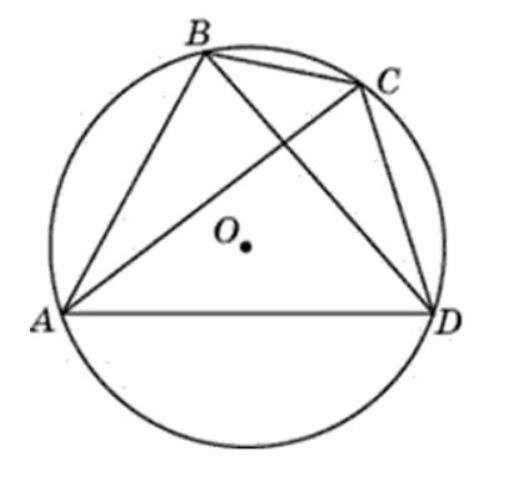
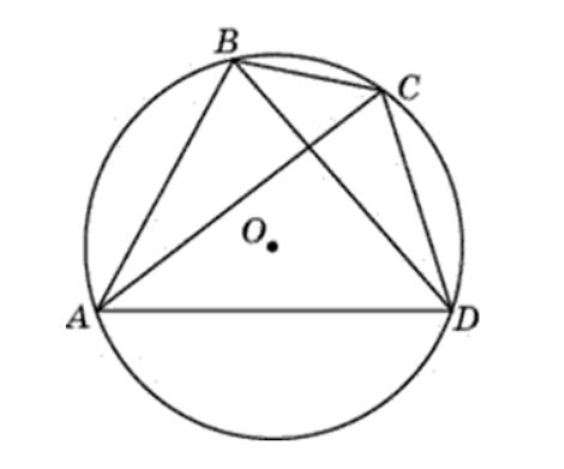
Дано: четырехугольник АВСД вписан в окружность. Ее центр – точка О. Нужно доказать, что
Нужно рассмотреть представленные фигуры. Аналогичным способом происходит доказательство для
(Ее часто называют обратной) Если в четырехугольнике
Доказательство Дана сумма противоположных углов четырехугольника ABCD, равная 180º.
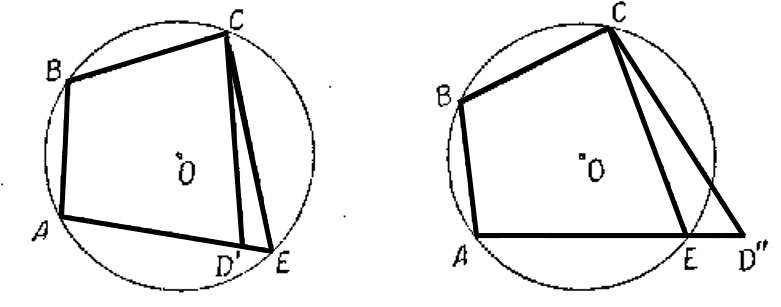
Из курса геометрии известно, что через 3 точки четырехугольника можно провести окружность. К примеру, можно задействовать точки A, B, C. Где будет находиться т. D? Имеются 3 предположения: Следует предположить, что D располагается внутри круга. Место указанной вершины занимает D´. Получается четырехугольник ABCD´. В результате следует:
Если продолжить AD´ до пересечения с имеющейся окружностью с центром в точке Е и соединить E и C, получится вписанный четырехугольник ABCE. Из первой теоремы следует равенство:
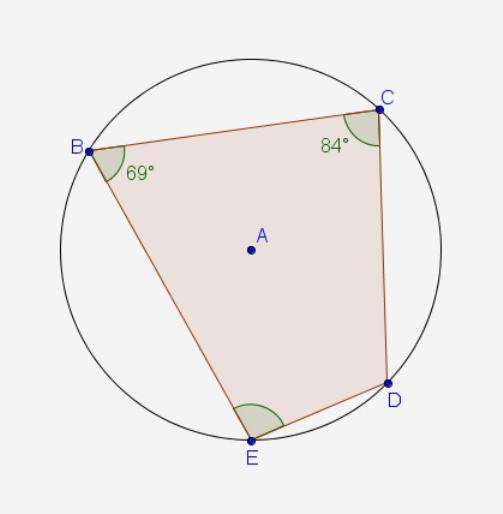
Согласно законам геометрии, выражение не имеет силы, поскольку Подобным образом можно доказать неправильность третьего предположения, когда D´´ выходит за границу описанной фигуры. Из двух гипотез вытекает единственно верная. Вершина D располагается на линии окружности. Другими словами, D совпадает с E. Отсюда следует, что все точки четырехугольника располагаются на описываемой линии. Из этих двух теорем вытекают следствия: Задача 1. В окружность вписан четырехугольник ABCD. Решение. Изначально может показаться, что найти ответ будет затруднительно. 1. Нужно вспомнить свойства из этой темы. А именно: сумма противоположных углов = 180º. В геометрии лучше придерживаться принципа: найти все, что можно. Потом пригодится. 2. Следующий шаг: использовать теорему о сумме углов треугольника. Ответ: Задача 2. Дан BCDE – вписанный четырехугольник в окружность.
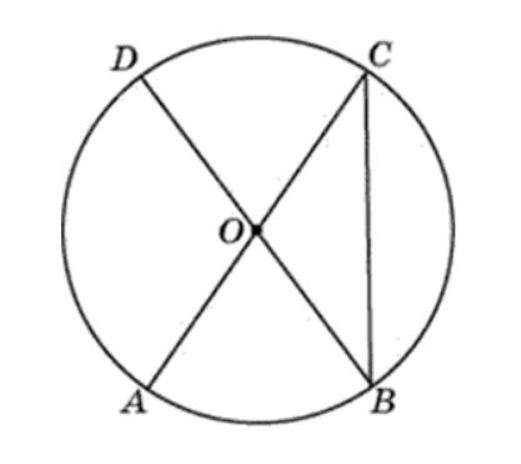
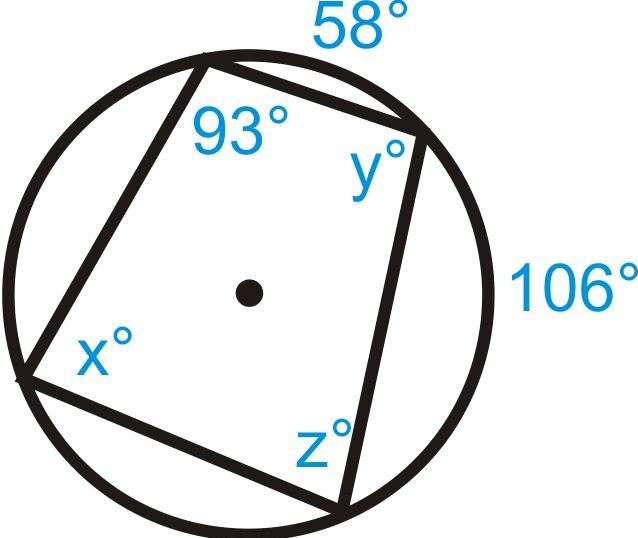
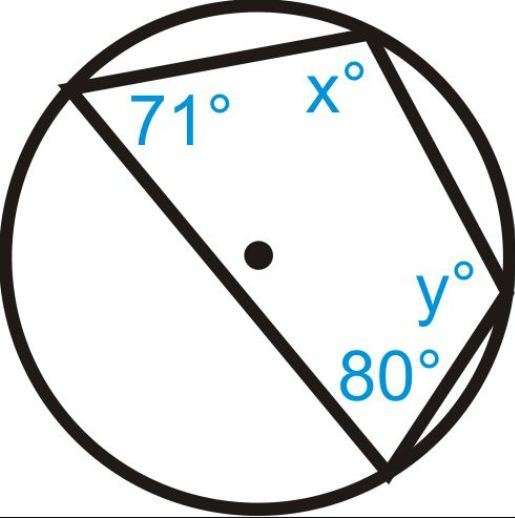
Решение. Ответ: < E = 96º. Задача 3. Дан вписанный четырехугольник в окружность. Данные указаны на рисунке. Необходимо найти неизвестные величины x, y, z. Решение: z = 180º – 93º = 87º (по Теореме 1) x = ½ * (58º + 106º) = 82º y = 180º – 82º = 98º (по Теореме 1) Ответ: z = 87º, x = 82º, y = 98º. Задача 4. Имеется вписанный четырехугольник в окружность. Величины указаны на рисунке. Найти x , y. Решение: x = 180º – 80º = 100º y = 180º – 71º = 109º Ответ: x = 100º, y = 109º. Пример 1. Дана окружность. Ее центр – точка О. АС и BD – диаметры. Пример 2. Даны четырехугольник ABCD и окружность, описанная вокруг него. Пример 3. Дана окружность и вписанный четырехугольник ABCD. Два его угла равны 82º и 58º. Необходимо найти больший из оставшихся углов и записать ответ в градусах. Пример 4. Дан четырехугольник ABCD. Углы А, В, С даны в соотношении 1:2:3. Необходимо найти угол D, если указанный четырехугольник может быть вписан в окружность. Ответ должен быть дан в градусах. Пример 5. Дан четырехугольник ABCD. Его стороны образуют дуги описанной окружности. Градусные величины AB, BC, CD и AD, соответственно, равны: 78˚, 107˚, 39˚, 136˚. Следует найти <С данного четырехугольника и записать ответ в градусах.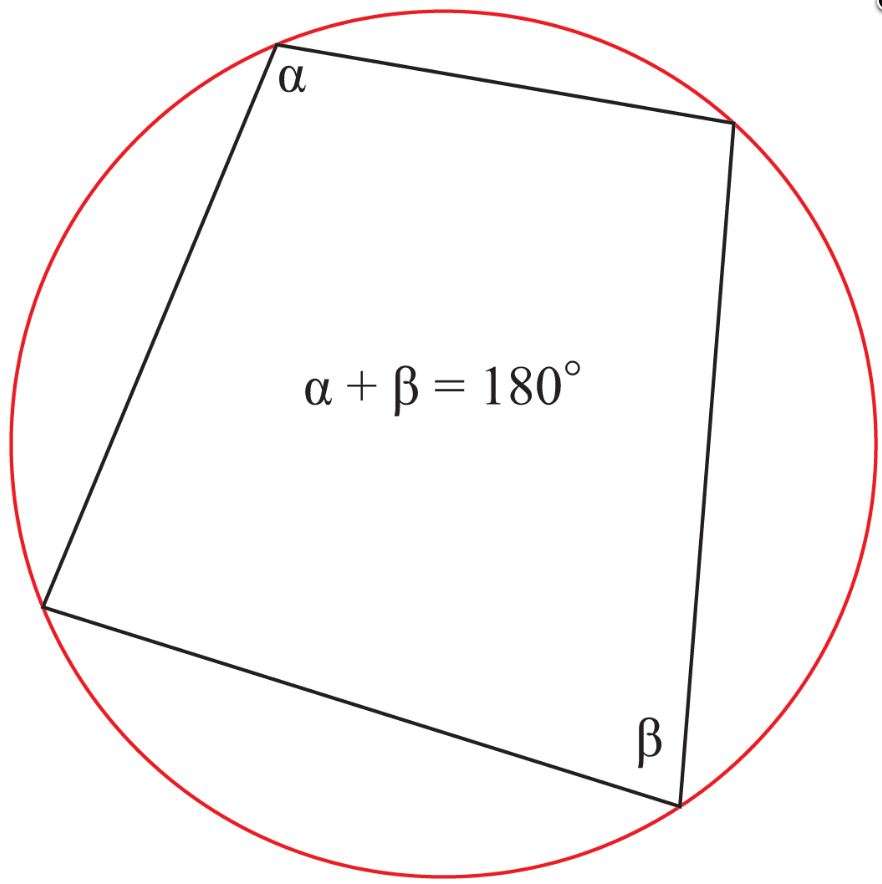
Теорема 2
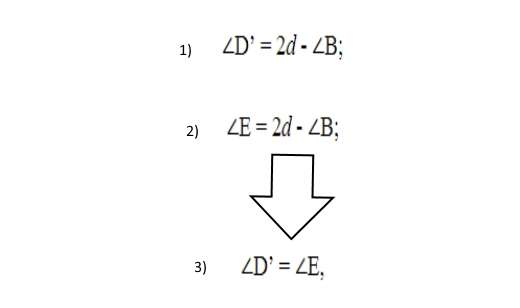
Несколько примеров
Задачи на самостоятельное решение