Рассмотрение в геометрии прямых и плоскостей предполагает изучение вопроса их взаимного расположения. В данной статье дадим определение перпендикуляра и наклонной к плоскости и прямой, а также рассмотрим свойства, которыми они обладают.
Уравнения для плоскости и прямой
К рассмотрению вопроса перпендикуляра и наклонной к разным геометрическим объектам нельзя переходить, пока не изучены математические способы задавания этих объектов. Речь идет о видах уравнений к плоскости и прямой.
 Вам будет интересно:Как стать математиком: эффективные методы обучения, необходимые навыки и умения
Вам будет интересно:Как стать математиком: эффективные методы обучения, необходимые навыки и умения
Прямая в пространстве, двумерном и трехмерном, часто задается в виде векторного уравнения. Оно имеет форму:
(x; y; z) = (x0; y0; z0) + λ*(a; b; c)
В первых скобках правой части равенства стоят координаты точки, принадлежащей прямой. Во вторых скобках находятся координаты вектора, являющегося направляющим для данного геометрического объекта. Параметр λ может принимать произвольное значение.
С данным уравнением легко работать в трехмерном случае. В случае двумерном оно также может быть использовано (только без координаты z). Однако в координатной плоскости прямая задается часто в ином виде:
A*x + B*y + C = 0
Здесь A, B, C – некоторые числа, причем (A; B) – это вектор, который перпендикулярен прямой. Это уравнение называется общим.
Плоскость как двумерный объект в пространстве чаще всего задается в общем виде, то есть:
A*x + B*y + C*z + D = 0
Важно не путать это уравнение с предыдущем. Здесь вектор, который задается координатами (A; B; C), оказывается нормальным (перпендикулярным) к плоскости, то есть является ее направляющим вектором.
Перпендикуляр для прямой и для плоскости
Изучение вопроса наклонной и перпендикуляра к прямой и плоскости начнем с перпендикулярного вектора. Выше уже было сказано, что для прямой на плоскости и для плоскости в трехмерном пространстве, которые заданы в виде уравнения общего вида, определить координаты перпендикулярного вектора не составляет труда. Главным его свойством, которое следует из определения перпендикуляра, является то, что он с рассматриваемым геометрическим объектом составляет угол 90o.
Синий отрезок на рисунке ниже является перпендикуляром к изображенной прямой.
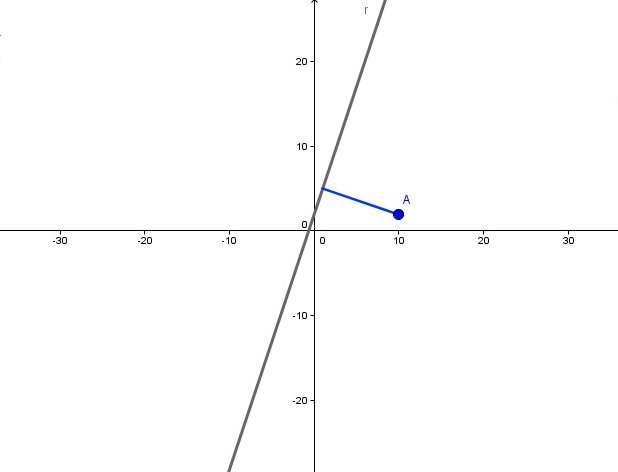
Еще одним свойством перпендикуляра к прямой является то, что его скалярное произведение с направляющим вектором будет равно нулю.
Перпендикуляр к плоскости, который представлен вектором и прямой, показан на рисунке ниже.
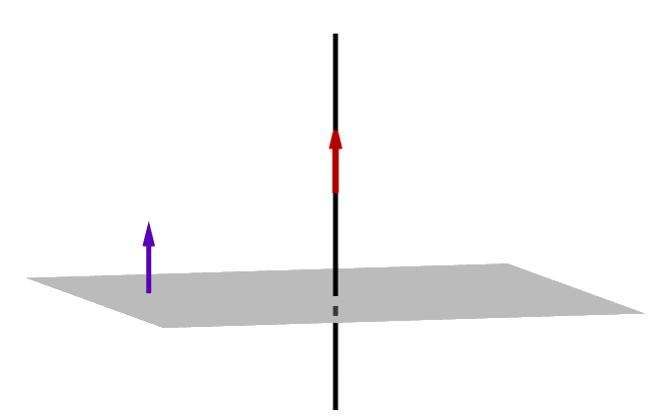
Так же, как и в случае с прямой, скалярное произведение этого перпендикуляра на любой вектор, принадлежащий плоскости, будет равно нулю.
Если для плоскости перпендикуляр не известен, то найти его несложно. Для этого необходимо вычислить векторное произведение любых двух не параллельных векторов, принадлежащих плоскости.
Нахождение перпендикуляра к плоскости и прямой важно, поскольку позволяет вычислить расстояние от указанных объектов к некоторой точке пространства.
Наклонная к прямой
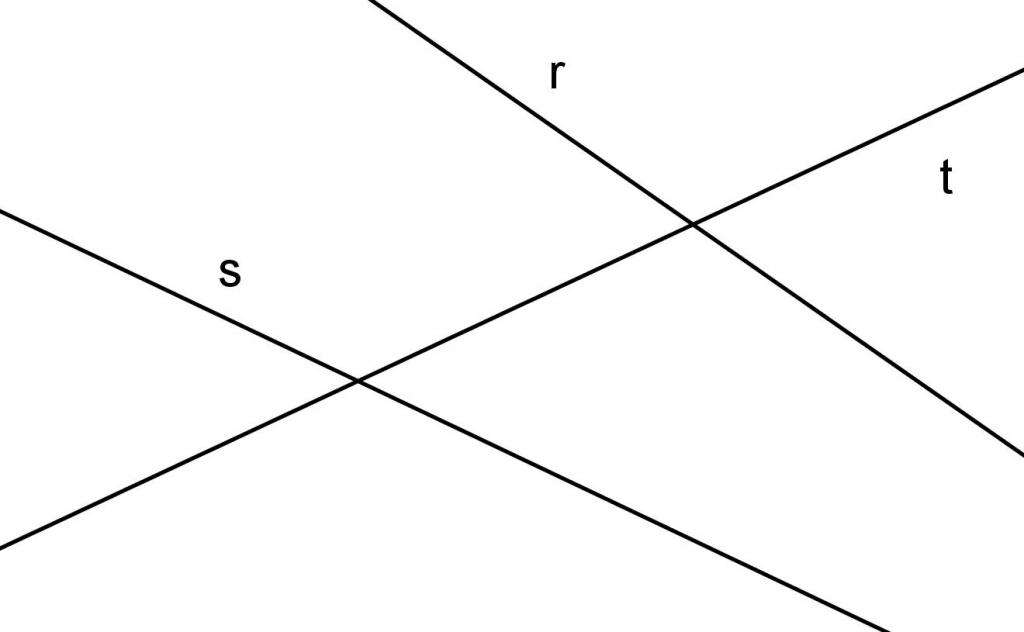
Продолжаем рассматривать свойства перпендикуляра и наклонной к прямой и плоскости. Дадим сначала определение наклонной для прямой. Под ней понимают любую прямую, которая пересекает данную под некоторым углом, не равным 90o.
Если из некоторой точки наклонной прямой опустить перпендикуляр на другую прямую, то отрезок, образованный точкой перпендикуляра и точкой пересечения объектов, будет проекцией отрезка наклонной на прямую.
Рассчитать угол φ между пересекающимися прямыми достаточно просто. Для этого пользуются формулой такой:
φ = arccos(|(v¯*u¯)|/(|v¯|*|u¯|))
Здесь v¯ и u¯ – это направляющие вектора рассматриваемых прямых.
Для случая на плоскости этой формулой можно пользоваться всегда без предварительных вычислений. В пространстве же следует учитывать, что прямые могут образовывать некоторый угол между собой, но при этом не пересекаться (быть скрещивающимися). В таком случае сначала следует проверить, имеют ли прямые общую точку пересечения.
Наклонная к плоскости
В вопросе перпендикуляра и наклонной остается рассмотреть наклонную к плоскости.
Любая прямая, которая пересекает заданную плоскость под некоторым острым углом, является наклонной к ней. Если каждую точку прямой проецировать на плоскость, проведя соответствующие перпендикуляры к ней, то мы получим проекцию всей прямой. Угол между этой проекцией и исходной прямой является углом пересечения рассматриваемых объектов.
Ниже на рисунке приводится прямая r, которая является наклонной к плоскости «пи».
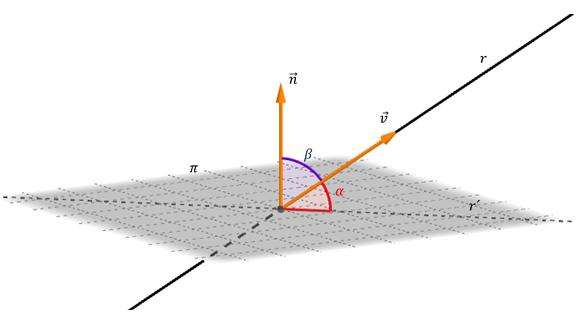
Прямая r' – это проекция r. Угол между «пи» и r обозначен как α. Для его определения пользуются следующей формулой:
α = arcsin(|(v¯*n¯)|/(|v¯|*|n¯|))
Где v¯ и n¯ – направляющие векторы прямой r и плоскости «пи» соответственно (см. рис.).
Пример задачи
Покажем, как можно использовать полученные знания о перпендикуляре и наклонной, чтобы решить следующую задачу:
Даны уравнения прямой и плоскости:
(x; y; z) = (1; 0; 2) + λ*(1; 1; 1);
x + 2*y – 1 = 0
Заданная прямая является наклонной к плоскости. Необходимо определить, под каким углом они пересекаются.
Выпишем координаты соответствующих направляющих векторов:
для прямой: v¯ = (1; 1; 1);
для плоскости: n¯ = (1; 2; 0)
Подставим эти координаты в формулу для угла α, получаем:
α = arcsin(|((1; 1; 1)*(1; 2; 0))|/(|(1; 2; 0)|*|(1; 1; 1)|)) =
= arcsin(3/(√5*√3)) ≈ 50,77o
Таким образом, прямая, являясь наклонной к плоскости, пересекает ее под углом 50,77o.
