Пирамида - это пространственный полиэдр, или многогранник, который встречается в геометрических задачах. Основными свойствами этой фигуры являются ее объем и площадь поверхности, которые вычисляются из знания любых двух ее линейных характеристик. Одной из таких характеристик является апофема пирамиды. О ней пойдет речь в статье.
Фигура пирамида
Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.
Вам будет интересно:«Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?
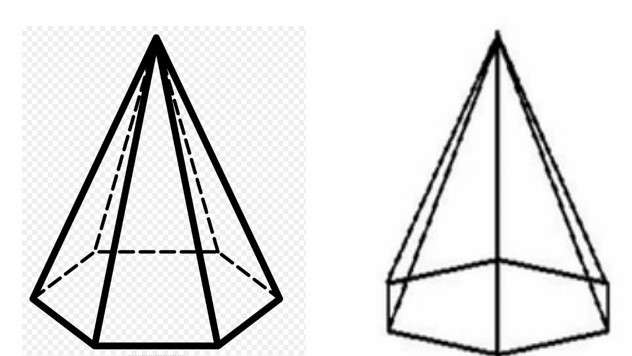
Всякая пирамида имеет вершину - точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.
Апофема правильной пирамиды
Ее также называют апотемой. Под ней понимают перпендикуляр, проведенный из вершины пирамиды к стороне основания фигуры. По своему определению этот перпендикуляр соответствует высоте треугольника, который образует боковую грань пирамиды.
Поскольку мы рассматриваем пирамиду правильную с n-угольным основанием, то все n апофем для нее будут одинаковыми, поскольку таковыми являются равнобедренные треугольники боковой поверхности фигуры. Заметим, что одинаковые апофемы являются свойством правильной пирамиды. Для фигуры общего типа (наклонной с неправильным n-угольником) все n апофем будут разными.
Еще одним свойством апофемы пирамиды правильной является то, что она одновременно является высотой, медианой и биссектрисой соответствующего треугольника. Это означает, что она делит его на два одинаковых прямоугольных треугольника.
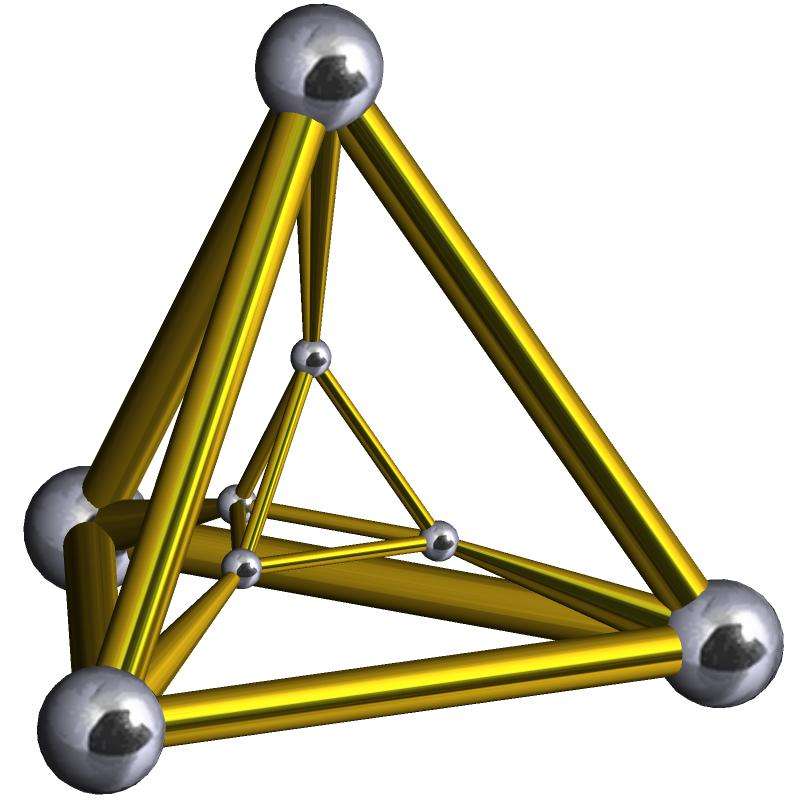
Треугольная пирамида и формулы для определения ее апофемы
В любой правильной пирамиде важными линейными характеристиками являются длина стороны ее основания, ребро боковое b, высота h и апофема hb. Эти величины друг с другом связаны соответствующими формулами, которые можно получить, если начертить пирамиду и рассмотреть необходимые прямоугольные треугольники.
Правильная треугольная пирамида состоит из 4 треугольных граней, причем одна из них (основание) должна быть обязательно равносторонней. Остальные являются равнобедренными в общем случае. Апофему треугольной пирамиды можно определить через другие величины по следующим формулам:
hb = √(b2 - a2/4);
hb = √(a2/12 + h2)
Первое из этих выражений справедливо для пирамиды с любым правильным основанием. Второе выражение характерно исключительно для треугольной пирамиды. Оно показывает, что апофема всегда больше высоты фигуры.
Не следует путать апофему пирамиды с таковой для многогранника. В последнем случае апофемой называется перпендикулярный отрезок, проведенный к стороне многогранника из его центра. Например, апофема равностороннего треугольника равна √3/6*a.
Задача на вычисление апофемы
Пусть дана правильная пирамида с треугольником в основании. Необходимо вычислить ее апофему, если известно, что площадь этого треугольника равна 34 см2, а сама пирамида состоит из 4 одинаковых граней.
В соответствии с условием задачи мы имеем дело с тетраэдром, состоящим из равносторонних треугольников. Формула для площади одной грани имеет вид:
S = √3/4*a2
Откуда получаем длину стороны a:
a = 2*√(S/√3)
Для определения апофемы hb воспользуемся формулой, содержащей боковое ребро b. В рассматриваемом случае его длина равна длине основания, имеем:
hb = √(b2 - a2/4) = √3/2*a
Подставляя значение a через S, получим конечную формулу:
hb = √3/2*2*√(S/√3) = √(S*√3)
Мы получили простую формулу, в которой апофема пирамиды зависит только от площади ее основания. Если подставить значение S из условия задачи, то получим ответ: hb ≈ 7,674 см.