Важной темой, изучаемой в физике, является проблема перемещения тел в пространстве. Они могут двигаться по прямолинейным и криволинейным траекториям. Одним из самых простых видов является перемещение при равноускоренном прямолинейном движении. Рассмотрим его в статье.
Механическое движение тел
Вопрос изменения пространственных координат в процессе перемещения объектов интересует людей с давних времен. Так, древнегреческий философ Архимед полагал, что движение не является естественной формой существования окружающих предметов. Действительно, любой брошенный предмет, в конце концов, останавливается. Архимед не знал о силах трения, поэтому считал, что истинным состоянием всех тел является покой. Такой точки зрения придерживался и другой философ Античной Греции, Зенон, который в своих знаменитых парадоксах доказывал, что движение является иллюзией и в действительности не существует.
 Вам будет интересно:Интеллектуальная школа Назарбаева в Казахстане
Вам будет интересно:Интеллектуальная школа Назарбаева в Казахстане
Только с приходом Нового времени теоретическое изучение вопроса движения вышло на следующий уровень. Важный вклад в исследование внес итальянец Галилео Галилей. Первый закон Ньютона в действительности сформулировал именно он. В своих трудах он отмечает, что всякое тело будет сохранять неизменными характеристики своего движения, если на него не воздействуют никакие внешние силы.
 Вам будет интересно:Основные этапы возникновения жизни согласно теории биопоэза
Вам будет интересно:Основные этапы возникновения жизни согласно теории биопоэза
Теорию классического механического движения, выраженную в кратких и понятных математических формулах, создал великий английский ученый Исаак Ньютон. В частности, второй закон, носящий его имя, дает исчерпывающую информацию для описания перемещения тел в пространстве.
Сила, ускорение и масса
Эти три физические величины входят в знаменитую формулу, известную каждому школьнику. Запишем ее:
F¯ = m*a¯
Здесь сила F¯ и ускорение a¯ являются векторными величинами, направленными в одну и ту же сторону. Коэффициент пропорциональности между ними - это масса тела m.
Записанная формула является основным выражением динамики. Сила является причиной изменения характеристик движения любого тела. Отсутствие внешней силы, оказывающей действие на тело, является достаточным условием для того, чтобы оно двигалось равномерно и прямолинейно.
Далее в статье рассмотрим формулы прямолинейного равноускоренного движения, которые описывают лишь результат действующих сил, то есть будем изучать перемещение тел с точки зрения кинематики.
Движение с постоянной скоростью
 Вам будет интересно:Плохие поступки и хорошие поступки детей
Вам будет интересно:Плохие поступки и хорошие поступки детей
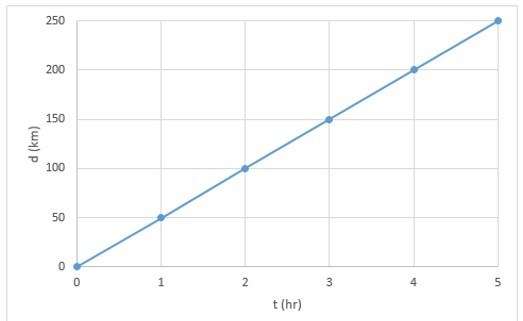
Перед тем, как рассматривать перемещение при прямолинейном равноускоренном движении, следует изучить его частный случай - равномерное изменение координат в пространстве. Прямолинейное равномерное движение математически описывается следующим равенством:
S = v*t
То есть путь, пройденный телом, пропорционален времени, в течение которого оно находится в движении, и скорости перемещения. Поскольку скорость измеряется в в системе СИ в метрах в секунду (м/с), а время в секундах (с), то путь рассчитывают в метрах (м).
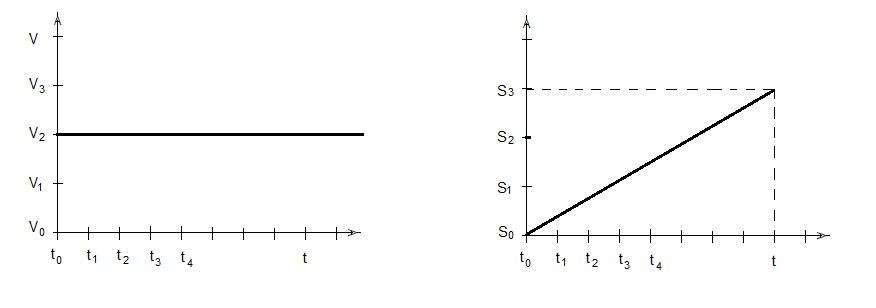
Особенностью данного вида движения является его прямолинейный характер, причем скорость остается постоянной в каждый момент времени (v = const.). Если нарисовать графики скорости и пути в зависимости от времени в двумерной прямоугольной системе координат, то в первом случае получится горизонтальная (параллельная оси x линия), а во втором случае - прямая, выходящая из начала координат, имеющая угловой коэффициент, равный скорости (k = v).
Прямолинейное равноускоренное движение: ускорение и скорость
Теперь предположим, что на находящееся в покое тело начала действовать сила. Согласно второму закону Ньютона, она вызовет ускорение тела. Скорость в этом случае будет изменяться по закону:
v = a*t
Это выражение говорит, что скорость, в отличие от равномерного движения, уже не будет величиной неизменной. Она растет с течением времени линейно. В свою очередь, ускорение a является постоянной величиной, поэтому движение называется равноускоренным, то есть происходящим с постоянным ускорением.
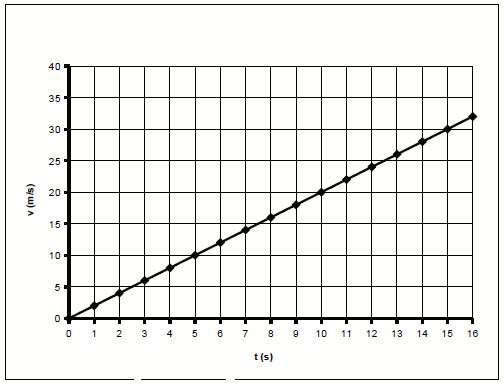
График скорости прямолинейного равноускоренного движения - это прямая линия, которая выходит из начала координат. Угловой ее коэффициент k равен ускорению a.
Равноускоренное движение с начальной скоростью
Формула прямолинейного равноускоренного движения, записанная для скорости в предыдущем пункте, не является общей. Дело в том, что при ее составлении полагалось, что тело в нулевой момент времени находится в покое, то есть v = 0. Однако в общем случае оно может двигаться равномерно со скоростью v0 ≠ 0, которая называется начальной. В этом случае предыдущую формулу для скорости можно переписать так:
v = v0 + a*t
Описываемое этим выражением движение можно представить следующим образом: тело, на которое не действовали силы, двигалось со скоростью v0. Затем возникла внешняя сила, направленная так же, как и начальная скорость, и привела к появлению ускорения a.
В записанном выражении время t отсчитывается от нуля. Поэтому при изображении графика скорости в данном случае получится аналогичная прямая, параллельная прямой для равноускоренного движения без начальной скорости. Однако она будет начинаться не с точки (0; 0), а с точки (0; v0).
Заметим, что если действующая на тело сила будет направлена против вектора начальной скорости, то имеет место равнозамедленное движение. В этом случае будет справедлива формула:
v = v0 - a*t
График этой функции - линия, которая стремится к нулевому значению v от начального значения v0. Точка, где график пересечет ось x (t), покажет время, когда тело остановится. Это время равно:
t = v0/a
Пройденный путь
Перемещение при прямолинейном равноускоренном движении означает, какой путь прошло тело за известный промежуток времени. Вычислить этот путь можно, если проинтегрировать по времени соответствующие выражения для скорости.
Путь при прямолинейном равноускоренном движении, когда начальная скорость отсутствует, определяется из выражения:
S = ∫t(v*dt) = a*t2/2
Поскольку ускорение a является постоянным для рассматриваемого типа движения, то пройденный путь возрастает как квадрат от времени. График равноускоренного прямолинейного движения для пути S представляет собой правую ветвь параболы, которая начинается в начале координат.
Теперь получим аналогичное выражение для пути S, только учтем, что до получения ускорения тело уже обладало скоростью v0. Тогда формула для S примет следующий вид:
S = ∫t(v*dt) = ∫t((v0 + a*t)*dt) = v0*t + a*t2/2.
Графиком этой функции S(t) также будет парабола, однако ее значения будут лежать выше, чем в предыдущем случае. Путь при равноускоренном движении, когда начальная скорость нулю не равна, можно рассматривать как наложение двух видов движения: равномерное и равноускоренное.
Наконец, если тело двигалось со скоростью v0, а затем начало замедлять свое движение с постоянным ускорением a, то формула для S примет вид:
S = ∫t(v*dt) = ∫t((v0 - a*t)*dt) = v0*t - a*t2/2.
Ниже на рисунке показаны графики для записанных в этом пункте формул для S.
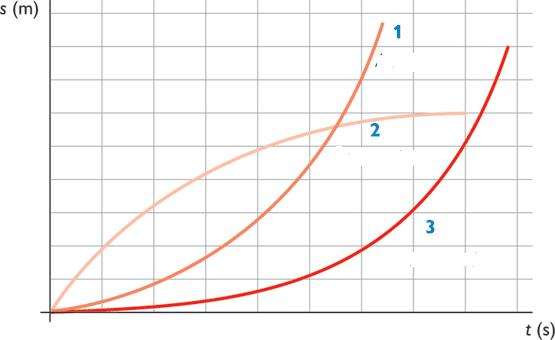
В первом случае речь идет об ускоренном движении с некоторой начальной скоростью, третий график - ускоренное движение без начальной скорости, а вторая кривая соответствует равнозамедленному движению. Видно, что две кривые 1 и 3 возрастают постоянно, но кривая 2 выходит на постоянное значение при некотором времени t. Это означает, что тело остановилось.
Примеры движения с ускорением
В быту можно привести ряд примеров перемещения при прямолинейном равноускоренном движении. Например, автомобиль, набирающий скорость после старта, самолет, который разгоняется на взлетной полосе, велосипедист, стремящийся остановиться (равнозамедленное).
Пожалуй, самым распространенным в природе движением с постоянным ускорением является падение тел в гравитационном поле нашей планеты. Если пренебречь силой трения воздуха, то процесс падения вблизи поверхности Земли происходит с ускорением 9,81 м/с2.
Далее покажем на примерах решения задач, как пользоваться приведенными формулами.
Задача с мотоциклистом
Известно, что расстояние между городами составляет 50 км. Мотоциклист преодолел это расстояние за 1 час. Известно, что 1/3 этого времени он двигался с постоянным ускорением, а 2/3 времени его скорость не изменялась. Необходимо вычислить конечную скорость, которую развил мотоциклист.
Для решения задачи воспользуемся следующими уравнениями прямолинейного равноускоренного движения:
S = a*(1/3*t)2/2 + v*2/3*t;
v = a*1/3*t
Где t - время, которое мотоциклист провел в пути. Подставляя второе выражение в первое, получаем значение ускорения a:
S = a*(1/3*t)2/2 + a*1/3*t*2/3*t =>
a = 18*S/(5*t2) = 18*50000/(5*3600*3600) ≈ 0,014 м/с
Двигаясь с этим ускорением в течение 20 минут, мотоциклист развил скорость:
v = a*1/3*t = 0,014*1/3*3600 = 16,8 м/с или около 60,5 км/ч
Задача с брошенным вверх мячом
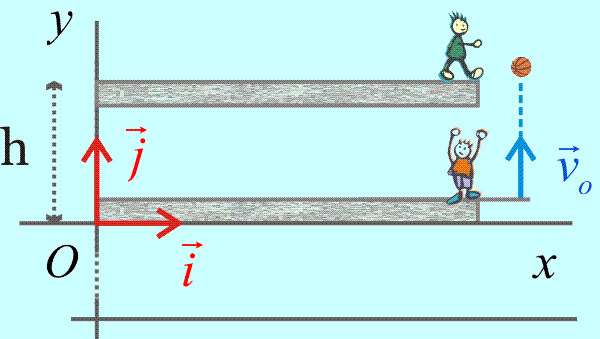
Мяч бросили вертикально вверх с начальной скоростью 10 м/с. Необходимо вычислить, на какую высоту он поднимется.
Речь идет о равнозамедленном движении с начальной скоростью v0. Если обозначить максимальную высоту подъема h, тогда для нее можно записать формулу:
h = v0*t - g*t2/2.
Здесь g = 9,81 м/с2, t - время подъема. Чтобы его определить, необходимо обратиться к условию, когда скорость тела v станет равна нулю:
v = v0 - g*t = 0 =>
t = v0/g.
Подставляя время t в формулу для h, получаем:
h = v02/g - g*v02/(2*g2) = v02/(2*g).
Подставляем сюда значение скорости из условия, получаем ответ: h ≈ 5,1 метра. Любопытно отметить, что высота подъема тела от его массы не зависит.