Динамика является одним из важных разделов физики, который изучает причины движения тел в пространстве. В данной статье рассмотрим с точки зрения теории одну из типичных задач динамики - движение тела по наклонной плоскости, а также приведем примеры решений некоторых практических проблем.
Основная формула динамики
Прежде чем переходить к изучению физики движения тела по плоскости наклонной, приведем необходимые теоретические сведения для решения этой задачи.
В XVII Исаак Ньютон благодаря практическим наблюдениям за движением макроскопических окружающих тел вывел три закона, носящих в настоящее время его фамилию. На этих законах зиждется вся классическая механика. Нас интересует в данной статье лишь второй закон. Его математический вид приведен ниже:
 Вам будет интересно:Эйлера теорема. Теорема Эйлера для простых многогранников
Вам будет интересно:Эйлера теорема. Теорема Эйлера для простых многогранников
F¯ = m × a¯.
Формула говорит о том, что действие внешней силы F¯ придаст ускорение a¯ телу массой m. Это простое выражение будем далее использовать для решения задач движения тела по плоскости наклонной.
Отметим, что сила и ускорение - это величины векторные, направленные в одну и ту же сторону. Кроме того, сила - это аддитивная характеристика, то есть в приведенной формуле F¯ можно рассматривать как результирующее воздействие на тело.
Наклонная плоскость и силы, действующие на тело, находящееся на ней
 Вам будет интересно:Антрополог Станислав Владимирович Дробышевский: биография и научная деятельность
Вам будет интересно:Антрополог Станислав Владимирович Дробышевский: биография и научная деятельность
Ключевым моментом, от которого зависит успех решения задач движения тела по плоскости наклонной, является определение действующих на тело сил. Под определением сил понимают знание их модулей и направлений действия.
Ниже дан рисунок, где показано, что тело (автомобиль) находится в покое на наклоненной под углом к горизонту плоскости. Какие силы на него действуют?
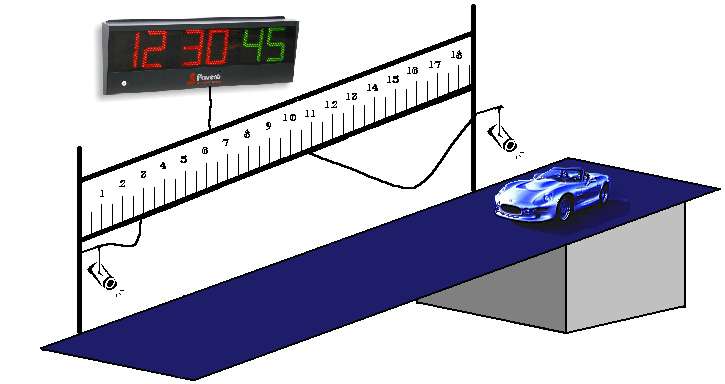
Список ниже перечисляет эти силы:
- тяжести;
- реакции опоры;
- трения;
- натяжения нити (если присутствует).
 Вам будет интересно:Педагогические теории: понятие и принципы
Вам будет интересно:Педагогические теории: понятие и принципы
Далее опишем подробнее каждую из них применительно к рассматриваемой задаче.
Сила тяжести

В первую очередь это сила тяжести (Fg). Она направлена вертикально вниз. Поскольку тело имеет возможность двигаться только вдоль поверхности плоскости, то при решении задач силу тяжести разлагают на две взаимно перпендикулярные составляющие. Одна из составляющих направлена вдоль плоскости, другая - перпендикулярна ей. Только первая из них приводит к появлению у тела ускорения и, по сути, является единственным движущим фактором для рассматриваемого тела. Вторая составляющая обуславливает возникновение силы реакции опоры.
Реакция опоры
Второй действующей на тело силой является реакция опоры (N). Причина ее появления связана с третьим законом Ньютона. Величина N показывает, с какой силой плоскость воздействует на тело. Она направлена вверх перпендикулярно плоскости наклонной. Если бы тело находилось на горизонтальной поверхности, то N равнялась бы его весу. В рассматриваемом же случае N равна лишь второй составляющей, полученной при разложении силы тяжести (см. абзац выше).
Реакция опоры не оказывает прямого воздействия на характер движения тела, поскольку она перпендикулярна плоскости наклона. Тем не менее она обуславливает появление трения между телом и поверхностью плоскости.
Сила трения
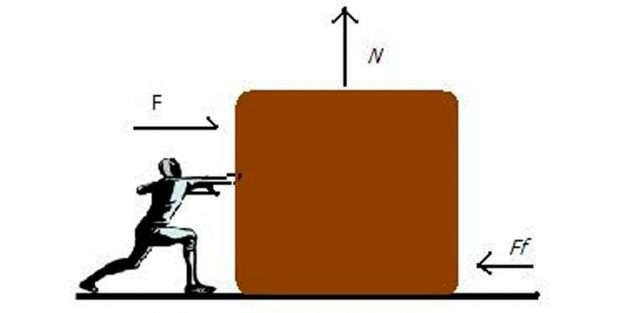
Третьей силой, которую следует учитывать при исследовании движения тела по наклонной плоскости, является трение (Ff). Физическая природа трения является непростой. Ее появление связано с микроскопическими взаимодействиями соприкасающихся тел, имеющих неоднородные поверхности контакта. Выделяют три вида этой силы:
- покоя;
- скольжения;
- качения.
Трение покоя и скольжения описываются одной и той же формулой:
Ff = µ × N,
где µ - это безразмерный коэффициент, значение которого определяется материалами трущихся тел. Так, при трении скольжения дерева о дерево µ = 0,4, а льда о лед - 0,03. Коэффициент для трения покоя всегда больше такового для скольжения.
Трение качения описывается по отличной от предыдущей формуле. Она имеет вид:
Ff = f × N / r.
Здесь r - радиус колеса, f - коэффициент, имеющий размерность обратной длины. Эта сила трения, как правило, намного меньше предыдущих. Заметим, что на ее значение влияет радиус колеса.
Сила Ff, какого бы типа она ни была, всегда направлена против движения тела, то есть Ff стремится остановить тело.
Натяжение нити
При решении задач движения тела по наклонной плоскости эта сила не всегда присутствует. Ее появление определяется тем, что находящееся на наклонной плоскости тело связано с помощью нерастяжимой нити с другим телом. Часто второе тело свисает на нити через блок за пределами плоскости.
На находящийся на плоскости предмет, сила натяжение нити воздействует либо ускоряя его, либо замедляя. Все зависит от модулей сил, действующих в физической системе.
Появление этой силы в задаче значительно усложняет процесс решения, поскольку приходится рассматривать одновременно движение двух тел (на плоскости и свисающего).

Далее приведем пример решения двух задач без участия силы натяжения нити.
Задача на определение критического угла
Теперь пришло время применить описанную теорию для решения реальных задач движения по наклонной плоскости тела.
Предположим, что брус из дерева имеет массу 2 кг. Он находится на деревянной плоскости. Следует определить, при каком критическом угле наклона плоскости брус начнет по ней скользить.
Скольжение бруса наступит только тогда, когда суммарная действующая вниз вдоль плоскости сила на него окажется больше нуля. Таким образом, чтобы решить эту задачу, достаточно определить результирующую силу и найти угол, при котором она станет больше нуля. Согласно условию задачи на брус будут вдоль плоскости оказывать действие только две силы:
- составляющая силы тяжести Fg1;
- трение покоя Ff.
Чтобы началось скольжение тела, должно выполняться условие:
Fg1 ≥ Ff.
Отметим, что если составляющая силы тяжести превысит трение покоя, то она также будет больше силы трения скольжения, то есть начавшееся движение будет продолжаться с постоянным ускорением.
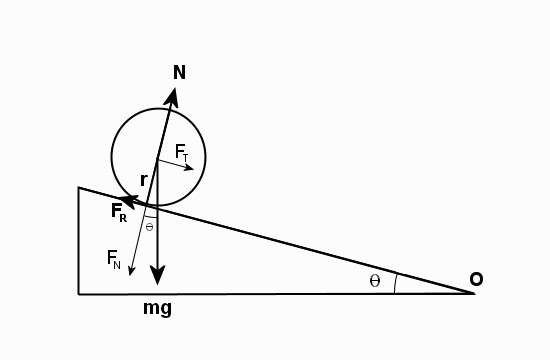
Рисунок ниже показывает направления всех действующих сил.
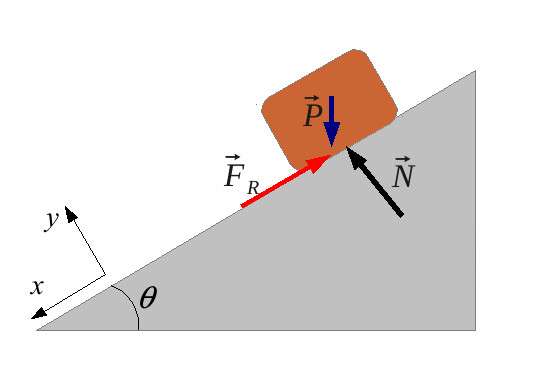
Обозначим критический угол символом θ. Несложно показать, что силы Fg1 и Ff будут равны:
Fg1 = m × g × sin(θ);
Ff = µ × m × g × cos(θ).
Здесь m × g - это вес тела, µ - коэффициент силы трения покоя для пары материалов дерево-дерево. Из соответствующей таблицы коэффициентов можно найти, что он равен 0,7.
Подставляем найденные величины в неравенство, получаем:
m × g × sin(θ) ≥ µ × m × g × cos(θ).
Преобразуя это равенство, приходим к условию движения тела:
tg(θ) ≥ µ =>
θ ≥ arctg(µ).
Мы получили весьма интересный результат. Оказывается, значение критического угла θ не зависит от массы тела на наклонной плоскости, а однозначно определяется коэффициентом трения покоя µ. Подставляя его значение в неравенство, получим величину критического угла:
θ ≥ arctg(0,7) ≈ 35o.
Задача на определение ускорения при движении по наклонной плоскости тела
Теперь решим несколько иную задачу. Пусть на стеклянной наклонной плоскости находится брус из дерева. Плоскость к горизонту наклонена под углом 45o. Следует определить, с каким ускорением будет двигаться тело, если его масса равна 1 кг.
Запишем главное уравнение динамики для этого случая. Поскольку сила Fg1 будет направлена вдоль движения, а Ff против него, то уравнение примет вид:
Fg1 - Ff = m × a.
Подставляем полученные в предыдущей задаче формулы для сил Fg1 и Ff, имеем:
m × g × sin(θ) - µ × m × g × cos(θ) = m × a.
Откуда получаем формулу для ускорения:
a = g × (sin(θ) - µ × cos(θ)).
Снова мы получили формулу, в которой нет массы тела. Этот факт означает, что бруски любой массы будут соскальзывать за одно и то же время по наклонной плоскости.
Учитывая, что коэффициент µ для трущихся материалов дерево-стекло равен 0,2, подставим все параметры в равенство, получим ответ:
a ≈ 5,55 м/с2.
Таким образом, методика решения задач с наклонной плоскостью заключается в определении результирующей силы, действующей на тело, и в последующем применении второго закона Ньютона.
